
24.(1)设碰撞前的速度为,根据机械能守恒定律
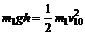 ①
①
设碰撞后m1与m2的速度分别为v1和v2,根据动量守恒定律
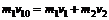 ②
②
由于碰撞过程中无机械能损失
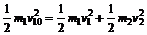 ③
③
②、③式联立解得
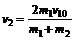 ④
④
将①代入得④
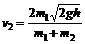
(2)a由④式,考虑到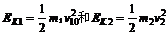 得
得
根据动能传递系数的定义,对于1、2两球
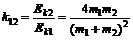 ⑤
⑤
同理可得,球m2和球m3碰撞后,动能传递系数k13应为
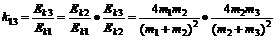 ⑥
⑥
依次类推,动能传递系数k1n应为
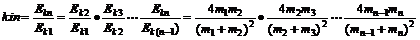
解得
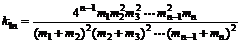
b.将m1=4m0,m3=mo代入⑥式可得
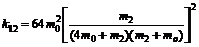
为使k13最大,只需使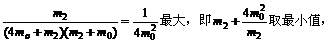
由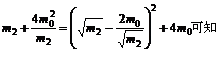
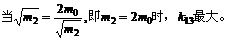
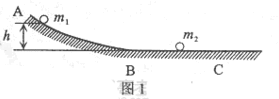
24.(09北京卷)(20分) 如图1所示,ABC为一固定在竖直平面内的光滑轨道,BC段水平,AB段与BC段平滑连接。质量为
如图1所示,ABC为一固定在竖直平面内的光滑轨道,BC段水平,AB段与BC段平滑连接。质量为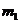 的小球从高位
的小球从高位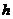 处由静止开始沿轨道下滑,与静止在轨道BC段上质量为
处由静止开始沿轨道下滑,与静止在轨道BC段上质量为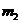 的小球发生碰撞,碰撞后两球两球的运动方向处于同一水平线上,且在碰撞过程中无机械能损失。求碰撞后小球
的小球发生碰撞,碰撞后两球两球的运动方向处于同一水平线上,且在碰撞过程中无机械能损失。求碰撞后小球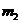 的速度大小
的速度大小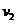 ;
;
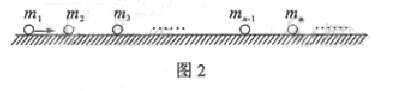
(2)碰撞过程中的能量传递规律在屋里学中有着广泛的应用。为了探究这一规律,我们才用多球依次碰撞、碰撞前后速度在同一直线上、且无机械能损失的恶简化力学模型。如图2所示,在固定光滑水平轨道上,质量分别为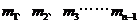 、
、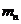 ……的若干个球沿直线静止相间排列,给第1个球初能
……的若干个球沿直线静止相间排列,给第1个球初能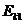 ,从而引起各球的依次碰撞。定义其中第
,从而引起各球的依次碰撞。定义其中第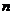 个球经过依次碰撞后获得的动能
个球经过依次碰撞后获得的动能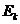 与
与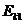 之比为第1个球对第
之比为第1个球对第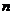 个球的动能传递系数
个球的动能传递系数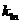
a 求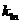
b 若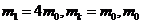 为确定的已知量。求
为确定的已知量。求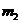 为何值时,
为何值时,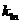 值最大
值最大
[解析]
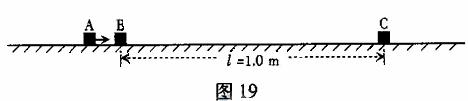
19.(09广东物理卷)(16分)如图19所示,水平地面上静止放置着物块B和C,相距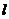 =1.0m 。物块A以速度
=1.0m 。物块A以速度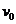 =10m/s沿水平方向与B正碰。碰撞后A和B牢固地粘在一起向右运动,并再与C发生正碰,碰后瞬间C的速度
=10m/s沿水平方向与B正碰。碰撞后A和B牢固地粘在一起向右运动,并再与C发生正碰,碰后瞬间C的速度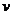 =2.0m/s 。已知A和B的质量均为m,C的质量为A质量的k倍,物块与地面的动摩擦因数
=2.0m/s 。已知A和B的质量均为m,C的质量为A质量的k倍,物块与地面的动摩擦因数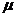 =0.45.(设碰撞时间很短,g取10m/s2)
=0.45.(设碰撞时间很短,g取10m/s2)
(1)计算与C碰撞前瞬间AB的速度;
(2)根据AB与C的碰撞过程分析k的取值范围,并讨论与C碰撞后AB的可能运动方向。
[解析]⑴设AB碰撞后的速度为v1,AB碰撞过程由动量守恒定律得 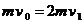
设与C碰撞前瞬间AB的速度为v2,由动能定理得 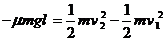
联立以上各式解得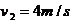
⑵若AB与C发生完全非弹性碰撞,由动量守恒定律得 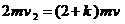
代入数据解得 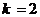
此时AB的运动方向与C相同
若AB与C发生弹性碰撞,由动量守恒和能量守恒得
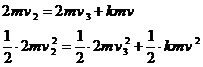
联立以上两式解得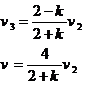
代入数据解得 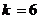
此时AB的运动方向与C相反
若AB与C发生碰撞后AB的速度为0,由动量守恒定律得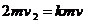
代入数据解得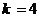
总上所述得 当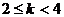 时,AB的运动方向与C相同
时,AB的运动方向与C相同
当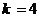 时,AB的速度为0
时,AB的速度为0
当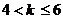 时,AB的运动方向与C相反
时,AB的运动方向与C相反
23.(16分)
解:
(1) 设起重机允许输出的最大功率为P0,重物达到最大速度时,拉力F0等于重力。
P0=F0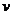 m
①
m
①
P0=mg ②
代入数据,有:P0=5.1×104W ③
说明:①式2分,②③式各1分。
(2) 匀加速运动结束时,起重机达到允许输出的最大功率,设此时重物受到的拉力为F,速度为v1,匀加速运动经历时间为t1,有:
P0=Fv1 ④
F-mg=ma ⑤
V1=at1 ⑥
由③④⑤⑥,代入数据,得:t1=5 s ⑦
t=2 s时,重物处于匀加速运动阶段,设此时速度为v2,输出功率为P,则
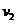 =at
⑧
=at
⑧
P=F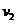 ⑨
⑨
由⑤⑧⑨,代入数据,得:P=2.04×104W ⑩
说明④⑤⑥⑦⑧⑨式各2分,⑦⑩式各1分。
23.(09四川卷)(16分)
 图示为修建高层建筑常用的塔式起重机。在起重机将质量m=5×103 kg的重物竖直吊起的过程中,重物由静止开始向上作匀加速直线运动,加速度a=0.2 m/s2,当起重机输出功率达到其允许的最大值时,保持该功率直到重物做vm=1.02 m/s的匀速运动。取g=10 m/s2,不计额外功。求:
图示为修建高层建筑常用的塔式起重机。在起重机将质量m=5×103 kg的重物竖直吊起的过程中,重物由静止开始向上作匀加速直线运动,加速度a=0.2 m/s2,当起重机输出功率达到其允许的最大值时,保持该功率直到重物做vm=1.02 m/s的匀速运动。取g=10 m/s2,不计额外功。求:
(1) 起重机允许输出的最大功率。
(2) 重物做匀加速运动所经历的时间和起重机在第2秒末的输出功率。
25.(09全国Ⅰ卷)(18分) 如图所示,倾角为θ的斜瓶上静止释放,质量均为m的木箱,相邻两木箱的距离均为l。工人用沿斜面的力推最小面的木箱使之上滑,逐一与其它木箱碰撞。每次碰撞后木箱都站在一起运动。整个过程中工人的推力不变,最后恰好能推着三个木箱匀速上滑。已知木箱与斜面向的动摩擦因数为p,重力加速度为g.设碰撞时间极短,求
(1)
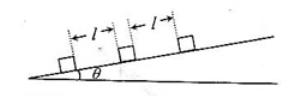 工人的推力;
工人的推力;
(2) 三个木箱均速运动的速度;
(3) 碰撞中损失的机械能。
答案(1)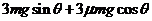
(2)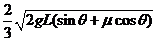
(3)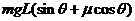
[解析](1)当匀速时,把三个物体看作一个整体受重力、推力F、摩擦力f和支持力.根据平衡的知识有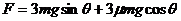
(2)第一个木箱与第二个木箱碰撞之前的速度为V1,加速度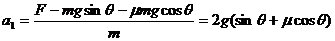 根据运动学公式或动能定理有
根据运动学公式或动能定理有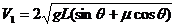 ,碰撞后的速度为V2根据动量守恒有
,碰撞后的速度为V2根据动量守恒有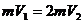 ,即碰撞后的速度为
,即碰撞后的速度为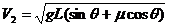 ,
,
然后一起去碰撞第三个木箱,设碰撞前的速度为V3
从V2到V3的加速度为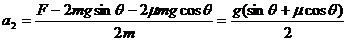 ,
,
根据运动学公式有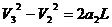 ,得
,得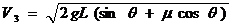 ,
,
跟第三个木箱碰撞根据动量守恒有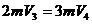 ,
,
得 就是匀速的速度.
就是匀速的速度.
(3)设第一次碰撞中的能量损失为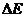 ,根据能量守恒有
,根据能量守恒有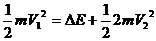 ,带入数据得
,带入数据得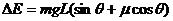 .
.

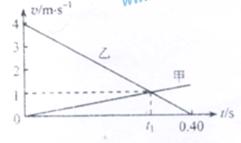
15、(09全国Ⅱ卷)两物体甲和乙在同一直线上运动,它们在0-0.4s时间内的v-t图象如图所示。若仅在两物体之间存在相互作用,则物体甲与乙的质量之比和图中时间t1分别为
 A.
A.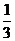 和0.30s B.3和0.30s
和0.30s B.3和0.30s

C.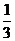 和0.28s D.3和0.28s
和0.28s D.3和0.28s
 答案B
答案B
 [解析]本题考查图象问题.根据速度图象的特点可知甲做匀加速,乙做匀减速.根据
[解析]本题考查图象问题.根据速度图象的特点可知甲做匀加速,乙做匀减速.根据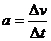 得
得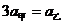 ,根据牛顿第二定律有
,根据牛顿第二定律有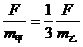 ,得
,得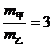 ,由
,由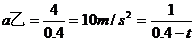 ,得t=0.3s,B正确.
,得t=0.3s,B正确.
(09福建卷) (2)一炮艇总质量为M,以速度
(2)一炮艇总质量为M,以速度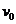 匀速行驶,从船上以相对海岸的水平速度
匀速行驶,从船上以相对海岸的水平速度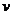 沿前进方向射出一质量为m的炮弹,发射炮弹后艇的速度为
沿前进方向射出一质量为m的炮弹,发射炮弹后艇的速度为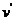 ,若不计水的阻力,则下列各关系式中正确的是
。(填选项前的编号)
,若不计水的阻力,则下列各关系式中正确的是
。(填选项前的编号)
 ①
①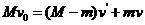 ②
② 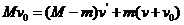 ③
③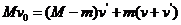 ④
④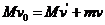
(2)动量守恒定律必须相对于同量参考系。本题中的各个速度都是相对于地面的,不需要转换。发射炮弹前系统的总动量为Mv0;发射炮弹后,炮弹的动量为mv0,船的动量为(M-m)v′所以动量守恒定律的表达式为
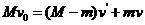
正确选项为①

21.(09全国Ⅰ卷)质量为M的物块以速度V运动,与质量为m的静止物块发生碰撞,碰撞后两者的动量正好相等,两者质量之比M/m可能为
A.2 B.3 C.4 D. 5
答案AB
[解析]本题考查动量守恒.根据动量守恒和能量守恒得设碰撞后两者的动量都为P,则总动量为2P,根据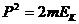 ,以及能量的关系得
,以及能量的关系得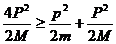 得
得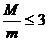 ,所以AB正确.
,所以AB正确.
22.(09北京卷)(16分) 已知地球半径为R,地球表面重力加速度为g,不考虑地球自转的影响。
已知地球半径为R,地球表面重力加速度为g,不考虑地球自转的影响。
(1) 推到第一宇宙速度v1的表达式;
(2) 若卫星绕地球做匀速圆周运动,运行轨道距离地面高度为h,求卫星的运行周期T。
[解析]
(1)设卫星的质量为m,地球的质量为M,
在地球表面附近满足 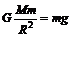
得 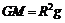 ①
①
卫星做圆周运动的向心力等于它受到的万有引力
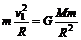 ②
②
①式代入②式,得到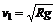
(2)考虑式,卫星受到的万有引力为
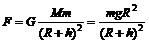 ③
③
由牛顿第二定律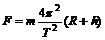 ④
④
③、④联立解得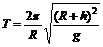
(09天津卷) 12.(20分)2008年12月,天文学家们通过观测的数据确认了银河系中央的黑洞“人马座A*”的质量与太阳质量的倍数关系。研究发现,有一星体S2绕人马座A*做椭圆运动,其轨道半长轴为9.50
12.(20分)2008年12月,天文学家们通过观测的数据确认了银河系中央的黑洞“人马座A*”的质量与太阳质量的倍数关系。研究发现,有一星体S2绕人马座A*做椭圆运动,其轨道半长轴为9.50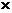 102天文单位(地球公转轨道的半径为一个天文单位),人马座A*就处在该椭圆的一个焦点上。观测得到S2星的运行周期为15.2年。
102天文单位(地球公转轨道的半径为一个天文单位),人马座A*就处在该椭圆的一个焦点上。观测得到S2星的运行周期为15.2年。
(1)  若将S2星的运行轨道视为半径r=9.50
若将S2星的运行轨道视为半径r=9.50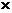 102天文单位的圆轨道,试估算人马座A*的质量MA是太阳质量Ms的多少倍(结果保留一位有效数字);
102天文单位的圆轨道,试估算人马座A*的质量MA是太阳质量Ms的多少倍(结果保留一位有效数字);
(2)  黑洞的第二宇宙速度极大,处于黑洞表面的粒子即使以光速运动,其具有的动能也不足以克服黑洞对它的引力束缚。由于引力的作用,黑洞表面处质量为m的粒子具有势能为Ep=-G
黑洞的第二宇宙速度极大,处于黑洞表面的粒子即使以光速运动,其具有的动能也不足以克服黑洞对它的引力束缚。由于引力的作用,黑洞表面处质量为m的粒子具有势能为Ep=-G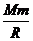 (设粒子在离黑洞无限远处的势能为零),式中M、R分别表示黑洞的质量和半径。已知引力常量G=6.7
(设粒子在离黑洞无限远处的势能为零),式中M、R分别表示黑洞的质量和半径。已知引力常量G=6.7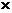 10-11N·m2/kg2,光速c=3.0
10-11N·m2/kg2,光速c=3.0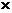 108m/s,太阳质量Ms=2.0
108m/s,太阳质量Ms=2.0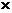 1030kg,太阳半径Rs=7.0
1030kg,太阳半径Rs=7.0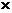 108m,不考虑相对论效应,利用上问结果,在经典力学范围内求人马座A*的半径RA与太阳半径
108m,不考虑相对论效应,利用上问结果,在经典力学范围内求人马座A*的半径RA与太阳半径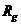 之比应小于多少(结果按四舍五入保留整数)。
之比应小于多少(结果按四舍五入保留整数)。
 答案(1)
答案(1)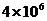 ,(2)
,(2)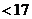
[解析]本题考查天体运动的知识。其中第2小题为信息题,如“黑洞”“引力势能”等陌生的知识都在题目中给出,考查学生提取信息,处理信息的能力,体现了能力立意。
(1)S2星绕人马座A*做圆周运动的向心力由人马座A*对S2星的万有引力提供,设S2星的质量为mS2,角速度为ω,周期为T,则
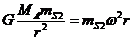 ①
①
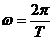 ②
②
设地球质量为mE,公转轨道半径为rE,周期为TE,则 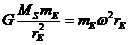 ③
③
综合上述三式得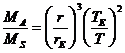
式中 TE=1年 ④ rE=1天文单位 ⑤
代入数据可得 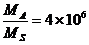 ⑥
⑥
(2)引力对粒子作用不到的地方即为无限远,此时料子的势能为零。“处于黑洞表面的粒子即使以光速运动,其具有的动能也不足以克服黑洞对它的引力束缚”,说明了黑洞表面处以光速运动的粒子在远离黑洞的过程中克服引力做功,粒子在到达无限远之前,其动能便减小为零,此时势能仍为负值,则其能量总和小于零,则有
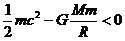 ⑦
⑦
依题意可知 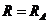 ,
,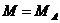
可得
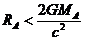 ⑧
⑧
代入数据得
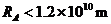 ⑨
⑨
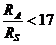 ⑩
⑩
机械能 动量 动量守恒定律的应用
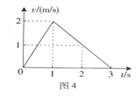
(09广东理基卷) 8.游乐场中的一滑梯如图3所示。小朋友从轨道顶端由静止开始下滑,沿水平轨道滑动
8.游乐场中的一滑梯如图3所示。小朋友从轨道顶端由静止开始下滑,沿水平轨道滑动 了一段距离后停下来,则
了一段距离后停下来,则
 A.下滑过程中支持力对小朋友做功
A.下滑过程中支持力对小朋友做功 B.下滑过程中小朋友的重力势能增加
B.下滑过程中小朋友的重力势能增加
 C.整个运动过程中小朋友的机械能守恒
C.整个运动过程中小朋友的机械能守恒 D.在水平华东过程中摩擦力对小朋友做负功
D.在水平华东过程中摩擦力对小朋友做负功
 答案.D
答案.D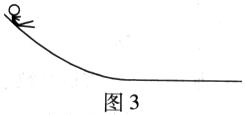
 [解析]在滑动的过程中,人受三个力重力做正功,势能降低B错,支持力不做功,摩擦力做负功,所以机械能不守恒,AC皆错.D正确.
[解析]在滑动的过程中,人受三个力重力做正功,势能降低B错,支持力不做功,摩擦力做负功,所以机械能不守恒,AC皆错.D正确.
 (09广东理基卷)
(09广东理基卷) 9.物体在合外力作用下做直线运动的
9.物体在合外力作用下做直线运动的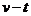 图像如图4所示
图像如图4所示
 A.在0-1s内,合外力做正功
A.在0-1s内,合外力做正功
 B.在0-2s 内,合外力总是做负功
B.在0-2s 内,合外力总是做负功
 C.在1-2s 内,合外力不做功
C.在1-2s 内,合外力不做功
 D.在0-3s内,合外力总是做正功
D.在0-3s内,合外力总是做正功
 答案.A
答案.A
 [解析]根据物体的速度图象可知,物体0-1s内做匀加速合外力做正功,A正确.1-3s内做匀减速合外力做负功.根据动能定理0到3s内,1-2s内合外力做功为零..
[解析]根据物体的速度图象可知,物体0-1s内做匀加速合外力做正功,A正确.1-3s内做匀减速合外力做负功.根据动能定理0到3s内,1-2s内合外力做功为零..
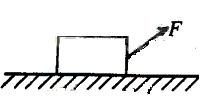 (09宁夏卷)21.水平地面上有一木箱,木箱与地面之间的动摩擦因数为
(09宁夏卷)21.水平地面上有一木箱,木箱与地面之间的动摩擦因数为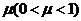 。现对木箱施加一拉力F,使木箱做匀速直线运动。设F的方向与水平面夹角为
。现对木箱施加一拉力F,使木箱做匀速直线运动。设F的方向与水平面夹角为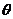 ,如图,在
,如图,在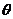 从0逐渐增大到90°的过程中,木箱的速度保持不变,则
从0逐渐增大到90°的过程中,木箱的速度保持不变,则
A.F先减小后增大 B.F一直增大
C.F的功率减小 D.F的功率不变
答案AC。
[解析]由于木箱的速度保持不变,因此木箱始终处于平衡状态,受力分析如图所示,则由平衡条件得: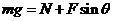 ,
,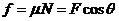 两式联立解得
两式联立解得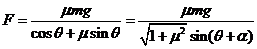 ,可见F有最小值,所以F先减小后增大,A正确;B错误;F的功率
,可见F有最小值,所以F先减小后增大,A正确;B错误;F的功率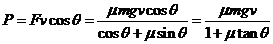 ,可见在
,可见在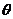 从0逐渐增大到90°的过程中tan
从0逐渐增大到90°的过程中tan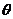 逐渐增大,则功率P逐渐减小,C正确,D错误。
逐渐增大,则功率P逐渐减小,C正确,D错误。
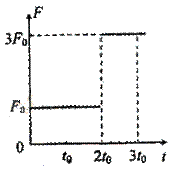 (09宁夏卷)17. 质量为m的物体静止在光滑水平面上,从t=0时刻开始受到水平力的作用。力的大小F与时间t的关系如图所示,力的方向保持不变,则
(09宁夏卷)17. 质量为m的物体静止在光滑水平面上,从t=0时刻开始受到水平力的作用。力的大小F与时间t的关系如图所示,力的方向保持不变,则
A.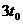 时刻的瞬时功率为
时刻的瞬时功率为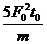
B.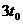 时刻的瞬时功率为
时刻的瞬时功率为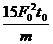
C.在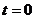 到
到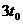 这段时间内,水平力的平均功率为
这段时间内,水平力的平均功率为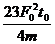
D. 在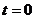 到
到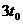 这段时间内,水平力的平均功率为
这段时间内,水平力的平均功率为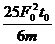
答案BD。
[解析]0-2t0 内物体的加速度为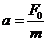 ,2t0
时刻的速度为
,2t0
时刻的速度为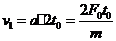 ,在3t0时刻的瞬时速度
,在3t0时刻的瞬时速度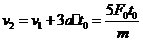 ,则
,则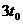 时刻的瞬时功率为
时刻的瞬时功率为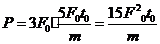 ,A错误;B正确;在
,A错误;B正确;在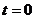 到
到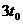 这段时间内,由动能定理可得
这段时间内,由动能定理可得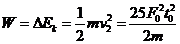 ,则这段时间内的平均功率
,则这段时间内的平均功率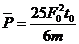 ,D正确。
,D正确。
(09 海南卷)
海南卷)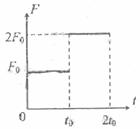 7.一物体在外力的作用下从静止开始做直线运动,合外力方向不变,大小随时间的变化如图所示。设该物体在
7.一物体在外力的作用下从静止开始做直线运动,合外力方向不变,大小随时间的变化如图所示。设该物体在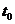 和
和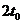 时刻相对于出发点的位移分别是
时刻相对于出发点的位移分别是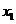 和
和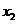 ,速度分别是
,速度分别是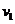 和
和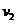 ,合外力从开始至
,合外力从开始至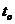 时刻做的功是
时刻做的功是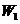 ,从
,从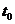 至
至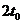 时刻做的功是
时刻做的功是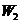 ,则
,则
A.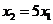
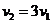 B.
B.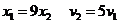
C.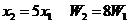 D.
D.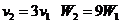 (09全国Ⅱ卷)20、以初速度竖直向上抛出一质量为m的小物体。假定物块所受的空气阻力f大小不变。已知重力加速度为g,则物体上升的最大高度和返回到原抛出点的速率分别为
(09全国Ⅱ卷)20、以初速度竖直向上抛出一质量为m的小物体。假定物块所受的空气阻力f大小不变。已知重力加速度为g,则物体上升的最大高度和返回到原抛出点的速率分别为
A、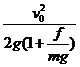 和
和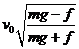 B、
B、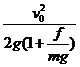 和
和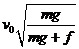
C、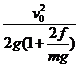 和
和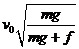 D、
D、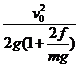 和
和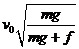
 答案A
答案A
 [解析]本题考查动能定理.上升的过程中,重力做负功,阻力
[解析]本题考查动能定理.上升的过程中,重力做负功,阻力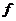 做负功,由动能定理得
做负功,由动能定理得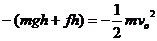 ,
,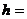
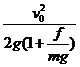 ,
,
求返回抛出点的速度由全程使用动能定理重力做功为零,只有阻力做功为有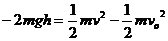 ,
,
解得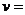
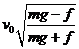 ,A正确
,A正确
15.(09宁夏卷) 地球和木星绕太阳运行的轨道都可以看作是圆形的。已知木星的轨道半径约为地球轨道半径的5.2倍,则木星与地球绕太阳运行的线速度之比约为
A. 0.19 B. 0.44 C. 2.3 D. 5.2
答案B。
 [解析]天体的运动满足万有引力充当向心力即
[解析]天体的运动满足万有引力充当向心力即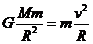 可知
可知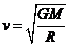 ,可见木星与地球绕太阳运行的线速度之比
,可见木星与地球绕太阳运行的线速度之比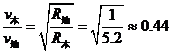 ,B正确。
,B正确。
(09广东理基卷) 10.关于地球的第一宇宙速度,下列表述正确的是
10.关于地球的第一宇宙速度,下列表述正确的是
 A.第一宇宙速度又叫环绕速度
A.第一宇宙速度又叫环绕速度
 B.第一宇宙速度又叫脱离速度
B.第一宇宙速度又叫脱离速度
 C.第一宇宙速度跟地球无关
C.第一宇宙速度跟地球无关
 D.第一宇宙速度跟地球的半径无关
D.第一宇宙速度跟地球的半径无关
 答案.A
答案.A
 [解析]第一宇宙速度又叫环绕速度A对,B错.根据定义有
[解析]第一宇宙速度又叫环绕速度A对,B错.根据定义有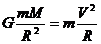 可知与地球的质量和半径有关.CD错.
可知与地球的质量和半径有关.CD错.
(09广东理基卷) 11.宇宙飞船在半径为
11.宇宙飞船在半径为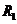 的轨道上运行,变轨后的半径为
的轨道上运行,变轨后的半径为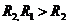 。宇宙飞船绕地球
。宇宙飞船绕地球 作匀速圆周运动,则变轨后宇宙飞船的
作匀速圆周运动,则变轨后宇宙飞船的
 A.线速度变小
B 角速度变小
A.线速度变小
B 角速度变小
 C.周期变大
D 向心加速度变大
C.周期变大
D 向心加速度变大
 答案.D
答案.D
 [解析]根据
[解析]根据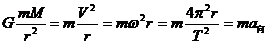 得
得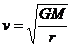 ,可知变轨后飞船的线速度变大,A错.角速度变大B错.周期变小C错.向心加速度在增大D正确.
,可知变轨后飞船的线速度变大,A错.角速度变大B错.周期变小C错.向心加速度在增大D正确.
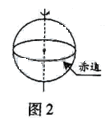 (09广东物理卷)5.发射人造卫星是将卫星以一定的速度送入预定轨道。发射场一般选择在尽可能靠近赤道的地方,如图2.这样选址的优点是,在赤道附近
(09广东物理卷)5.发射人造卫星是将卫星以一定的速度送入预定轨道。发射场一般选择在尽可能靠近赤道的地方,如图2.这样选址的优点是,在赤道附近
A.地球的引力较大
B.地球自转线速度较大
C.重力加速度较大
D.地球自转角速度较大
[答案]B。
[解析]由于发射卫星需要将卫星以一定的速度送入运动轨道,在靠进赤道处的地面上的物体的线速度最大,发射时较节能,因此B正确。
(09全国Ⅱ卷)26(21分)如图,P、Q为某地区水平地面上的两点,在P点正下方一球形区域内储藏有石油,假定区域周围岩石均匀分布,密度为。石油密度远小于,可将上述球形区域视为空腔如果没有这一空腔,则该地区重力加速度,(正常值)沿竖直方向,当存在空腔时,该地区重力加速度的大小和方向会与正常情况有微小偏高,重力回速度在原坚直方向(即PO方向)上的投影相对于正常值的偏离叫做“重力加速度反常”为了探寻石油区域的位置和石油储量,常利用P点到附近重力加速度反常现象,已知引力常数为G
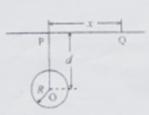
(1) 设球形空腔体积为F,球心深度为d远小于地球半径R,PQ=x求空腔所引起的Q点处的重力加速度反常
(2) 若在水平地面上半径L的范围内发现,重力加速度反常值在S与KS,K>1之间变化,且重力加速度反常的最大值出现在半为L的范围的中心,如果这种反常是于地下存在某一球形空腔造成的,试求此球形空腔球心的深度和空腔的体积

 答案(1)
答案(1)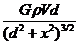
 (2)
(2)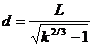 ,
,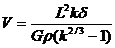

 [解析]本题考查万有引力部分的知识.
[解析]本题考查万有引力部分的知识.
 (1)如果将近地表的球形空腔填满密度为
(1)如果将近地表的球形空腔填满密度为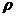 的岩石,则该地区重力加速度便回到正常值.因此,重力加速度反常可通过填充后的球形区域产生的附加引力
的岩石,则该地区重力加速度便回到正常值.因此,重力加速度反常可通过填充后的球形区域产生的附加引力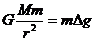 ………①来计算,式中的m是Q点处某质点的质量,M是填充后球形区域的质量,
………①来计算,式中的m是Q点处某质点的质量,M是填充后球形区域的质量,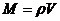 ……………②
……………②
 而r是球形空腔中心O至Q点的距离
而r是球形空腔中心O至Q点的距离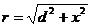 ………③
………③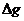 在数值上等于由于存在球形空腔所引起的Q点处重力加速度改变的大小.Q点处重力加速度改变的方向沿OQ方向,重力加速度反常
在数值上等于由于存在球形空腔所引起的Q点处重力加速度改变的大小.Q点处重力加速度改变的方向沿OQ方向,重力加速度反常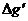 是这一改变在竖直方向上的投影
是这一改变在竖直方向上的投影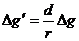 ………④联立以上式子得
………④联立以上式子得

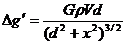 ,…………⑤
,…………⑤
 (2)由⑤式得,重力加速度反常
(2)由⑤式得,重力加速度反常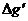 的最大值和最小值分别为
的最大值和最小值分别为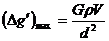 ……⑥
……⑥

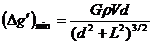 ……………⑦由提设有
……………⑦由提设有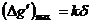 、
、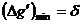 ……⑧
……⑧
 联立以上式子得,地下球形空腔球心的深度和空腔的体积分别为
联立以上式子得,地下球形空腔球心的深度和空腔的体积分别为

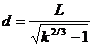 ,
,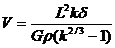
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com