
31.(2009四川卷文)(本小题满分12分)
已知函数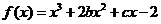 的图象在与
的图象在与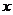 轴交点处的切线方程是
轴交点处的切线方程是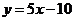 。
。
(I)求函数 的解析式;
的解析式;
(II)设函数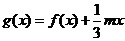 ,若
,若 的极值存在,求实数
的极值存在,求实数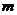 的取值范围以及函数
的取值范围以及函数 取得极值时对应的自变量
取得极值时对应的自变量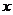 的值.
的值.
解析 (I)由已知,切点为(2,0),故有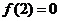 ,即
,即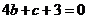 ……①
……①
又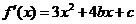 ,由已知
,由已知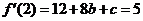 得
得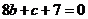 ……②
……②
联立①②,解得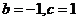 .
.
所以函数的解析式为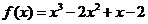 …………………………………4分
…………………………………4分
(II)因为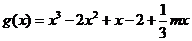
令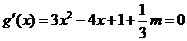
当函数有极值时,则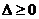 ,方程
,方程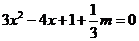 有实数解,
有实数解, 

由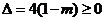 ,得
,得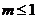 .
.
①当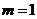 时,
时,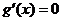 有实数
有实数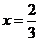 ,在
,在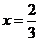 左右两侧均有
左右两侧均有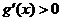 ,故函数
,故函数 无极值
无极值
②当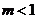 时,
时,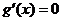 有两个实数根
有两个实数根
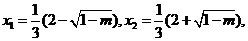
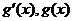 情况如下表:
情况如下表:
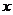 |
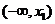 |
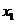 |
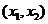 |
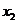 |
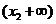 |
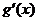 |
+ |
0 |
- |
0 |
+ |
 |
↗ |
极大值 |
↘ |
极小值 |
↗ |
所以在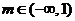 时,函数
时,函数 有极值;
有极值;
当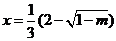 时,
时, 有极大值;当
有极大值;当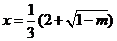 时,
时, 有极小值;
有极小值;
…………………………………12分
30.(2009湖北卷理)(本小题满分14分) (注意:在试题卷上作答无效)
在R上定义运算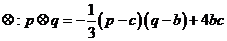 (b、c为实常数)。记
(b、c为实常数)。记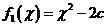 ,
,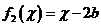 ,
,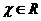 .令
.令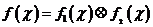 .
.
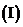 如果函数
如果函数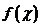 在
在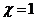 处有极什
处有极什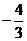 ,试确定b、c的值;
,试确定b、c的值;
 求曲线
求曲线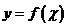 上斜率为c的切线与该曲线的公共点;
上斜率为c的切线与该曲线的公共点;
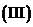 记
记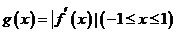 的最大值为
的最大值为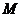 .若
.若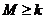 对任意的b、c恒成立,试示
对任意的b、c恒成立,试示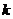 的最大值。
的最大值。
解 当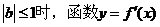 得对称轴x=b位于区间
得对称轴x=b位于区间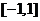 之外
之外 

此时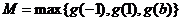
由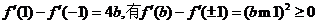
①若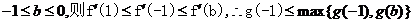
于是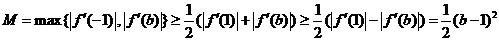
①若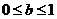 ,则
,则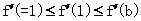 ,
,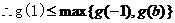
于是
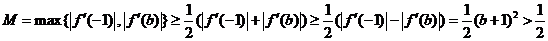
综上,对任意的b、c都有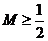
而当,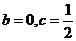 时,
时,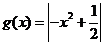 在区间
在区间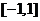 上的最大值
上的最大值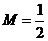


故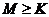 对任意的b,c恒成立的k的最大值为
对任意的b,c恒成立的k的最大值为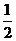
28.(2009天津卷文)(本小题满分12分)
设函数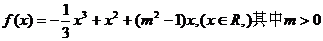
(Ⅰ)当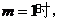 曲线
曲线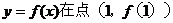 处的切线斜率
处的切线斜率
(Ⅱ)求函数的单调区间与极值;
(Ⅲ)已知函数 有三个互不相同的零点0,
有三个互不相同的零点0,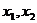 ,且
,且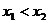 。若对任意的
。若对任意的
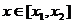 ,
,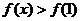 恒成立,求m的取值范围。
恒成立,求m的取值范围。
答案 (1)1(2) 在
在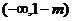 和
和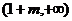 内减函数,在
内减函数,在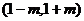 内增函数。函数
内增函数。函数 在
在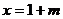 处取得极大值
处取得极大值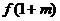 ,且
,且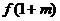 =
=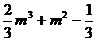
函数 在
在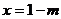 处取得极小值
处取得极小值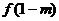 ,且
,且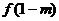 =
=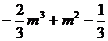
解析 解析 当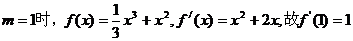
所以曲线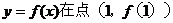 处的切线斜率为1.
处的切线斜率为1. 

(2)解析 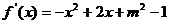 ,令
,令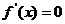 ,得到
,得到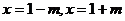
因为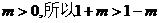
当x变化时,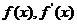 的变化情况如下表:
的变化情况如下表:
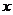 |
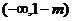 |
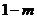 |
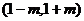 |
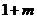 |
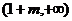 |
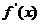 |
+ |
0 |
- |
0 |
+ |
 |
  |
极小值 |
 |
极大值 |
  |
 在
在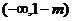 和
和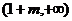 内减函数,在
内减函数,在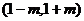 内增函数。
内增函数。
函数 在
在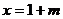 处取得极大值
处取得极大值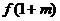 ,且
,且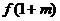 =
=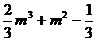
函数 在
在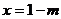 处取得极小值
处取得极小值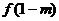 ,且
,且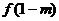 =
=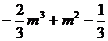
(3)解析 由题设, 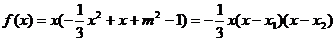
所以方程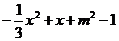 =0由两个相异的实根
=0由两个相异的实根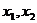 ,故
,故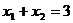 ,且
,且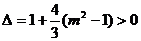 ,解得
,解得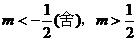
因为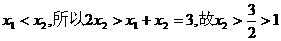
若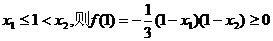 ,而
,而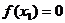 ,不合题意
,不合题意
若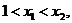 则对任意的
则对任意的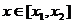 有
有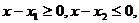
则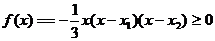 又
又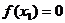 ,所以函数
,所以函数 在
在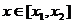 的最小值为0,于是对任意的
的最小值为0,于是对任意的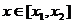 ,
,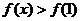 恒成立的充要条件是
恒成立的充要条件是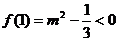 ,解得
,解得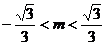


综上,m的取值范围是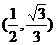
[考点定位]本小题主要考查导数的几何意义,导数的运算,以及函数与方程的根的关系解不等式等基础知识,考查综合分析问题和解决问题的能力。
27.(2009江西卷理)(本小题满分12分)
设函数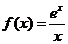
(1)求函数 的单调区间;
的单调区间;
(1)若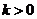 ,求不等式
,求不等式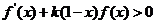 的解集.
的解集.
解析 (1)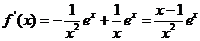 ,
由
,
由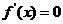 ,得
,得 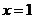 .
.
因为 当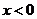 时,
时,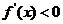 ;
当
;
当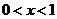 时,
时,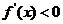 ;
当
;
当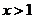 时,
时, ;
;
所以 的单调增区间是:
的单调增区间是: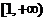 ;
单调减区间是:
;
单调减区间是: 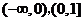 .
.
(2)由 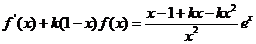
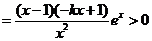 ,
,
得: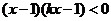 .
.
故:当 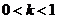 时, 解集是:
时, 解集是: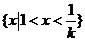 ;
;
当 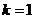 时,解集是:
时,解集是: 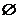 ;
;
当 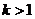 时, 解集是:
时, 解集是: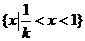 .
.
26.(2009江西卷文)(本小题满分12分)
设函数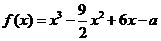 .
.
(1)对于任意实数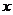 ,
,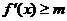 恒成立,求
恒成立,求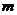 的最大值;
的最大值;
(2)若方程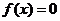 有且仅有一个实根,求
有且仅有一个实根,求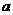 的取值范围.
的取值范围.
解析 (1) 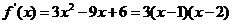 ,
,
因为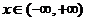 ,
,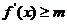 ,
即
,
即 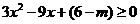 恒成立,
恒成立,
所以 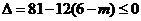 , 得
, 得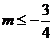 ,即
,即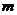 的最大值为
的最大值为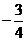
(2) 因为 当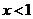 时,
时,  ;当
;当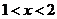 时,
时, 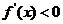 ;当
;当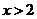 时,
时,  ;
;
所以 当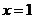 时,
时, 取极大值
取极大值 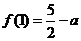 ;
;
当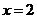 时,
时, 取极小值
取极小值 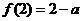 ;
;
故当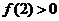 或
或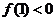 时, 方程
时, 方程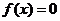 仅有一个实根. 解得
仅有一个实根. 解得 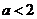 或
或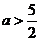 .
.
25.(2009安徽卷文)(本小题满分14分)
已知函数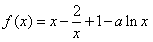 ,a>0,
,a>0,
(Ⅰ)讨论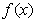 的单调性;
的单调性;
(Ⅱ)设a=3,求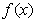 在区间{1,
在区间{1,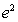 }上值域。期中e=2.71828…是自然对数的底数。
}上值域。期中e=2.71828…是自然对数的底数。
[思路]由求导可判断得单调性,同时要注意对参数的讨论,即不能漏掉,也不能重复。第二问就根据第一问中所涉及到的单调性来求函数 在
在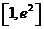 上的值域。
上的值域。
解析 (1)由于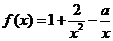
令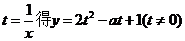
①当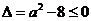 ,即
,即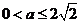 时,
时, 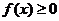 恒成立.
恒成立.
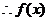 在(-∞,0)及(0,+∞)上都是增函数.
在(-∞,0)及(0,+∞)上都是增函数.
②当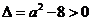 ,即
,即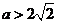 时
时 

由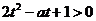 得
得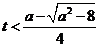 或
或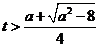
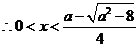 或
或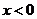 或
或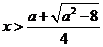
又由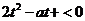 得
得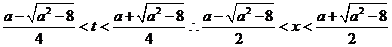
综上①当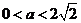 时,
时,  在
在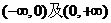 上都是增函数.
上都是增函数.
②当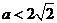 时,
时,  在
在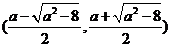 上是减函数,
上是减函数, 

在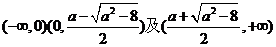 上都是增函数.
上都是增函数.
(2)当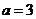 时,由(1)知
时,由(1)知 在
在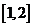 上是减函数.
上是减函数.
在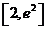 上是增函数.
上是增函数.
又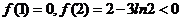
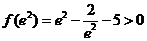


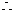 函数
函数 在
在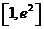 上的值域为
上的值域为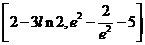
24.(2009安徽卷理)(本小题满分12分)
已知函数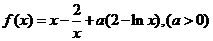 ,讨论
,讨论 的单调性.
的单调性.
本小题主要考查函数的定义域、利用导数等知识研究函数的单调性,考查分类讨论的思想方法和运算求解的能力。本小题满分12分。
解析  的定义域是(0,+
的定义域是(0,+ ),
),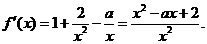


设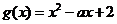 ,二次方程
,二次方程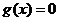 的判别式
的判别式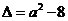 .
.
当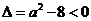 ,即
,即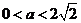 时,对一切
时,对一切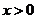 都有
都有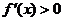 ,此时
,此时 在
在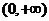 上是增函数。
上是增函数。
①当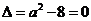 ,即
,即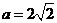 时,仅对
时,仅对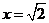 有
有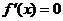 ,对其余的
,对其余的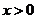 都有
都有
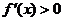 ,此时
,此时 在
在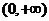 上也是增函数。
上也是增函数。
① 当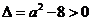 ,即
,即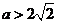 时,
时,
方程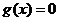 有两个不同的实根
有两个不同的实根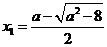 ,
,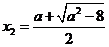 ,
,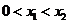 .
.
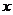 |
 |
 |
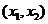 |
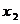 |
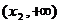 |
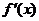 |
+ |
0 |
_ |
0 |
+ |
 |
单调递增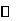 |
极大 |
单调递减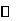 |
极小 |
单调递增 |
此时 在
在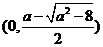 上单调递增, 在
上单调递增, 在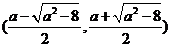 是上单调递减, 在
是上单调递减, 在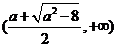 上单调递增.
上单调递增.
23.(2009广东卷理)(本小题满分14分)
已知二次函数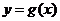 的导函数的图像与直线
的导函数的图像与直线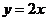 平行,且
平行,且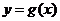 在
在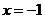 处取得极小值
处取得极小值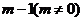 .设
.设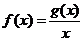 .
.
(1)若曲线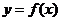 上的点
上的点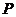 到点
到点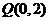 的距离的最小值为
的距离的最小值为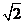 ,求
,求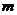 的值;
的值;
(2)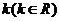 如何取值时,函数
如何取值时,函数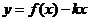 存在零点,并求出零点.
存在零点,并求出零点.
解析 (1)依题可设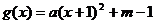 (
(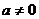 ),则
),则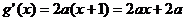 ;
;
又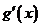 的图像与直线
的图像与直线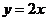 平行
平行 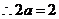
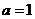
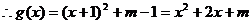 ,
, 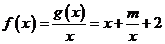 ,
,
设 ,则
,则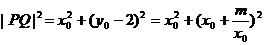


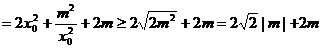
当且仅当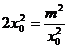 时,
时,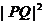 取得最小值,即
取得最小值,即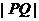 取得最小值
取得最小值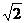
当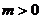 时,
时,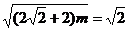 解得
解得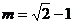
当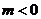 时,
时,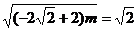 解得
解得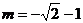
(2)由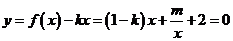 (
(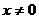 ),得
),得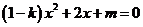

当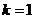 时,方程
时,方程 有一解
有一解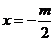 ,函数
,函数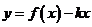 有一零点
有一零点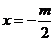 ;
;
当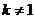 时,方程
时,方程 有二解
有二解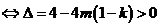 ,
,
若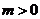 ,
,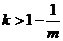 ,
,
函数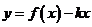 有两个零点
有两个零点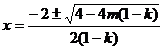 ,即
,即
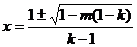 ;
;
若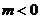 ,
,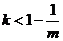 ,
,
函数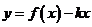 有两个零点
有两个零点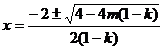 ,即
,即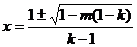 ;
;
当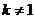 时,方程
时,方程 有一解
有一解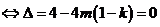 ,
, 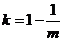 ,
,
函数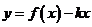 有一零点
有一零点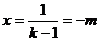
综上,当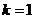 时, 函数
时, 函数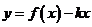 有一零点
有一零点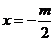 ;
;
当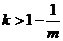 (
(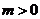 ),或
),或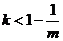 (
(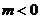 )时,
)时,
函数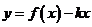 有两个零点
有两个零点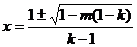 ;
;
当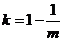 时,函数
时,函数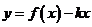 有一零点
有一零点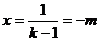 .
.
22.设函数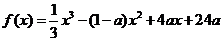 ,其中常数a>1
,其中常数a>1
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)若当x≥0时,f(x)>0恒成立,求a的取值范围。
解析 本题考查导数与函数的综合运用能力,涉及利用导数讨论函数的单调性,第一问关键是通过分析导函数,从而确定函数的单调性,第二问是利用导数及函数的最值,由恒成立条件得出不等式条件从而求出的范围。
解析 (I)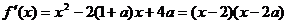
由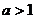 知,当
知,当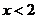 时,
时,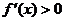 ,故
,故 在区间
在区间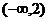 是增函数;
是增函数;
当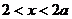 时,
时,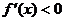 ,故
,故 在区间
在区间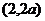 是减函数;
是减函数;
当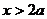 时,
时,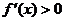 ,故
,故 在区间
在区间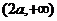 是增函数。
是增函数。
综上,当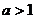 时,
时, 在区间
在区间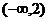 和
和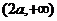 是增函数,在区间
是增函数,在区间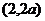 是减函数。
是减函数。
(II)由(I)知,当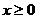 时,
时, 在
在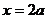 或
或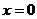 处取得最小值。
处取得最小值。
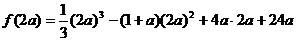
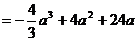
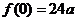
由假设知
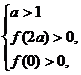 即
即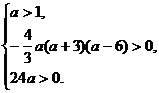 解得 1<a<6
解得 1<a<6
故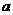 的取值范围是(1,6)
的取值范围是(1,6)
22.(2009山东卷文)(本小题满分12分)
已知函数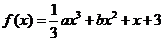 ,其中
,其中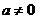
(1)当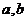 满足什么条件时,
满足什么条件时, 取得极值?
取得极值?
(2)已知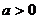 ,且
,且 在区间
在区间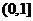 上单调递增,试用
上单调递增,试用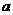 表示出
表示出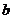 的取值范围.
的取值范围.
解: (1)由已知得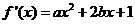 ,令
,令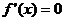 ,得
,得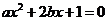 ,
,
 要取得极值,方程
要取得极值,方程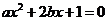 必须有解,
必须有解,
所以△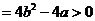 ,即
,即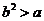 , 此时方程
, 此时方程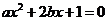 的根为
的根为
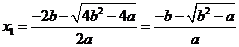 ,
,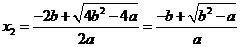 ,
,
所以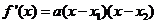
当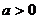 时,
时,
|
x |
(-∞,x1) |
x 1 |
(x1,x2) |
x2 |
(x2,+∞) |
|
f’(x) |
+ |
0 |
- |
0 |
+ |
|
f (x) |
增函数 |
极大值 |
减函数 |
极小值 |
增函数 |
所以 在x 1, x2处分别取得极大值和极小值.
在x 1, x2处分别取得极大值和极小值.
当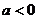 时,
时,
|
x |
(-∞,x2) |
x 2 |
(x2,x1) |
x1 |
(x1,+∞) |
|
f’(x) |
- |
0 |
+ |
0 |
- |
|
f (x) |
减函数 |
极小值 |
增函数 |
极大值 |
减函数 |
所以 在x 1, x2处分别取得极大值和极小值.
在x 1, x2处分别取得极大值和极小值.
综上,当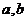 满足
满足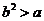 时,
时,  取得极值.
取得极值.
(2)要使 在区间
在区间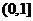 上单调递增,需使
上单调递增,需使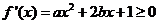 在
在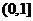 上恒成立.
上恒成立.
即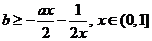 恒成立, 所以
恒成立, 所以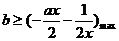
设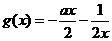 ,
,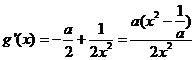 ,
,
令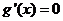 得
得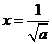 或
或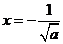 (舍去),
(舍去),
当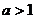 时,
时,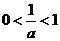 ,当
,当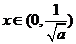 时
时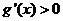 ,
,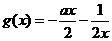 单调增函数;
单调增函数;
当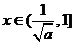 时
时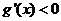 ,
,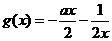 单调减函数,
单调减函数,
所以当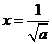 时,
时, 取得最大,最大值为
取得最大,最大值为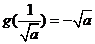 .
.
所以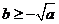
当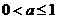 时,
时,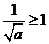 ,此时
,此时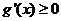 在区间
在区间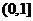 恒成立,所以
恒成立,所以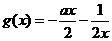 在区间
在区间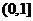 上单调递增,当
上单调递增,当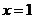 时
时 最大,最大值为
最大,最大值为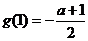 ,所以
,所以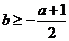
综上,当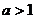 时,
时, 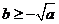 ; 当
; 当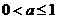 时,
时, 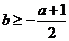
[命题立意]:本题为三次函数,利用求导的方法研究函数的极值、单调性和函数的最值,函数在区间上为单调函数,则导函数在该区间上的符号确定,从而转为不等式恒成立,再转为函数研究最值.运用函数与方程的思想,化归思想和分类讨论的思想解答问题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com