
⑴若各物体加速度相同,则
∑F=(mA+mB )a
或正交分解法
 ∑Fx=(mA+mB )ax
∑Fx=(mA+mB )ax
∑Fy=(mA+mB )ay
⑵若各物体加速度不相同,则
 ∑Fx=mAaAx+mBaBx
∑Fx=mAaAx+mBaBx
∑Fy=mAaAy+mBaBy
常用来研究A、B中有一个加速度为零的情况:
 若aB=0,则: ∑Fx=mAaAx
若aB=0,则: ∑Fx=mAaAx
∑Fy=mAaAy
[典题例析]
 例1.如图所示,一个质量为M的物体放在光滑的水平桌面上,当用20N的力F通过细绳绕过定滑轮拉它时,产生2m/s2的加速度.现撤掉20N拉力,而在细绳下端挂上重为20N的物体m,如图,则物体M的加速度为
m/s2,前、后两种情况下绳的张力分别为
.(取g=10 m/s2)
例1.如图所示,一个质量为M的物体放在光滑的水平桌面上,当用20N的力F通过细绳绕过定滑轮拉它时,产生2m/s2的加速度.现撤掉20N拉力,而在细绳下端挂上重为20N的物体m,如图,则物体M的加速度为
m/s2,前、后两种情况下绳的张力分别为
.(取g=10 m/s2)
例2.如图所示,质量为m2的物体2放在正沿平直轨道向右行驶的车厢底板上,并用竖直细绳通过光滑定滑轮连接质量为m1的物体,与物体1相连接的绳与竖直方向成θ角,则 ( B D )
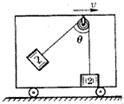 A.车厢的加速度为
A.车厢的加速度为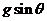
B.绳对物体1的拉力为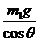
C.底板对物体2的支持力为(m2-m1)g
D.物体2所受底板的摩擦力为m2gtanθ
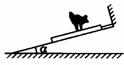
例3.如图所示,在倾角为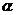 的固定光滑斜面上,有一用绳子拴着的长木板,木板上站着一只猫,已知木板的质量是猫的质量的2倍.当绳子突然断开时,猫立即沿着板向上跑,以保持其相对斜面的位置不变.则此时木板沿斜面下滑的加速度为 ( C )
的固定光滑斜面上,有一用绳子拴着的长木板,木板上站着一只猫,已知木板的质量是猫的质量的2倍.当绳子突然断开时,猫立即沿着板向上跑,以保持其相对斜面的位置不变.则此时木板沿斜面下滑的加速度为 ( C )
 A.
A.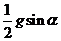 B.
B.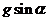
C.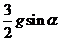 D.
D.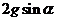
例4.质量为M的小车放在光滑水平面上,小车上用细线悬挂另一质量为m的小球,且M>m.用一力F水平向右拉小球,使小球和车一起以加速度a向右运动,细线与竖直方向成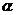 角,细线的拉力为F1.若用一力F'水平向左拉小车,使小球和车一起以加速度a'向左运动时,细线与竖直方向也成
角,细线的拉力为F1.若用一力F'水平向左拉小车,使小球和车一起以加速度a'向左运动时,细线与竖直方向也成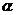 角,细线的拉力为F2,则 ( B )
角,细线的拉力为F2,则 ( B )
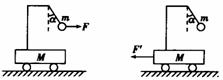 A.a'=a,F2=F1 B.a'>a,F2=F1
A.a'=a,F2=F1 B.a'>a,F2=F1
C.a'<a,F2=F1 D.a'>a,F2>F1
例5.如图所示,两个用轻线相连的位于光滑水平面上的物块,质量分别为m1和m2,拉力F1和F2方向相反,与轻线沿同一水平直线,且F1>F2,试求在两个物块运动过程中轻线的拉力T。

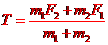
例6.一人在井下站在吊台上,用如图所示的定滑轮装置拉绳把吊台和自己提升上来.图中跨过滑轮的两段绳都认为是竖直的且不计摩擦.吊台的质量m=15kg,人的质量为M=55kg,起动时吊台向上的加速度是a=0.2m/s2,求这时人对吊台的压力.(g=9.8m/s2)
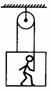
(200N,方向竖直向下)
例7.两重叠在一起的滑块,置于固定的且倾角为θ的斜面上,如图所示,滑块A、B的质量分别为m和M,B与斜面间的动摩擦因数为μ1,A与B之间的动摩擦因数为μ2,两滑块接触面与斜面平行,并都从静止开始以相同的加速度从斜面滑下,则滑块A受到的摩擦力( AD )
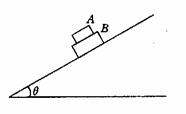 A.大小等于μ1mgcosθ B.大小等于μ2mgcosθ
A.大小等于μ1mgcosθ B.大小等于μ2mgcosθ
C.等于零 D.方向沿斜面向上
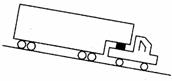
例8.如图所示,一辆汽车A拉着装有集装箱的拖车B,以速度v1=30 m/s进入向下倾斜的直车道.车道每100m下降2m.为了使汽车速度在x=200 m的距离内减到v2=10 m/s,驾驶员必须刹车.假定刹车时地面的摩擦阻力是恒力,且该力的70%作用于拖车B,30%作用于汽车A.已知A的质量m1=2000kg,B的质量m2=6000kg.求汽车与拖车的连接处沿运动方向的相互作用力.(取重力加速度g=10m/s2)(880N)
[问题反思]
第5课时 牛顿运动定律的应用(三)
(超重和失重问题)
[知识回顾]
1.超重:当物体具有 的加速度时(包括向上加速或向下减速两种情况),物体对支持物的压力或对悬挂物的拉力 自身重力的现象。
2.整体法:把构成连接体的各个物体视为一整体,从而转化为单一物体的动力学问题。
通常情况下,连接体在运动方向上有一个共同的加速度,而另一方向上加速度为零。
则 ∑F=(mA+mB )a
或正交分解法
 ∑Fx=(mA+mB )ax
∑Fx=(mA+mB )ax
∑Fy=0
研究此系统的受力或运动时,应用牛顿运动定律求解问题的关键是研究对象的选取和转换.一般若讨论的问题不涉及系统内部的作用力时,可以以整个系统为研究对象列方程求解;若涉及系统中各物体间的相互作用,则应以系统的某一部分为对象列方程求解,这样,便将物体间的内力转化为外力,从而体现出其作用效果,使问题得以求解.在求解连接体问题时,整体法和隔离法相互依存,相互补充交替使用.
整体法和隔离法是相辅相成的.本来单用隔离法就可解决连接问题,但如果这两种方法交叉使用,则处理问题十分方便,例如当系统中各物体有相同加速度,要求系统中某两物体间的相互作用力时,往往是先用整体法求出加速度,再用隔离法求出两物体间的相互作用力.
1.隔离法:把构成连接体的各个物体隔离开来,分别视为单一物体,转化为简单的动力学问题。
2.外力和内力
如果以物体系为研究对象,受到系统之外的作用力,这些力是系统受到的 力,而系统内各物体间的相互作用力为 。
应用牛顿第二定律列方程不考虑 力。如果把物体隔离出来作为研究对象,则这些内力将转换为隔离体的 力。
3连接体问题的分析方法
(1)整体法:连接体中的各物体如果 ,求加速度时可以把连接体作为一个整体。运用 列方程求解。
(2)隔离法:如果要求连接体间的相互作用力,必须隔离其中一个物体,对该物体应用 求解,此法称为隔离法。
(3)整体法与隔离法是相对统一,相辅相成的。本来单用隔离法就可以解决的连接体问题,但如果这两种方法交叉使用,则处理问题就更加方便。如当系统中各物体有相同的加速度,求系统中某两物体间的相互作用力时,往往是先用 法求出 ,再用 法求 。
[考点突破]
考点 连接体问题
1.连接体与隔离体
两个或两个以上物体相连接组成的物体系统,称为 。如果把其中某个物体隔离出来,该物体即为 。
4.4;7420)
[问题反思]
第4课时 牛顿运动定律的应用(二)
(连接体问题)
[知识回顾]
1.7)
例10.如图所示,一质量为500 kg的木箱放在质量为2000 kg的平板车的后部,木箱到驾驶室的距离L=1.6 m,已知木箱与木板间的动摩擦因数μ=0.484,平板车在运动过程中所受阻力是车和箱总重的0.20倍,平板车以v0=22.0m/s的速度行驶,为不让木箱撞击驾驶室,g取10 m/s2,试求:
⑴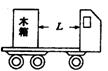 从刹车开始到平板车完全停止至少要经过多长时间?
从刹车开始到平板车完全停止至少要经过多长时间?
⑵驾驶员刹车时的制动力不能超过多大?
例7.如图所示,质量为m=10kg物体在F=200N的水平推力作用下,从粗糙斜面的底端由静止开始沿斜面运动,斜面固定不动,与水平地面的夹角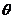 =37°,力F作用2s后撤去,物体在斜面上继续上滑了1.25s后,速度减为零。求:物体与斜面间的动摩擦因数和物体的总位移。
=37°,力F作用2s后撤去,物体在斜面上继续上滑了1.25s后,速度减为零。求:物体与斜面间的动摩擦因数和物体的总位移。
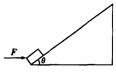
0.25;16.25m)
例8.质量为40kg的雪撬在倾角θ=37°的斜面上向下滑动如图甲所示,所受的空气阻力与速度成正比。今测得雪撬运动的v-t图象如图乙所示,且AB是曲线的切线,B点坐标为(4,15),CD是曲线的渐近线。试求空气的阻力系数k和雪撬与斜坡间的动摩擦因数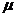 。
。
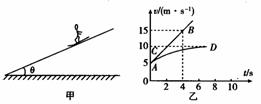
(20N s/m;0.125)
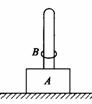
例9.如图所示,底座上装有长0.5m的直立杆,其总质量为0.2kg,杆上套有质量为0.05kg的小环B,它与杆之间有摩擦.当环从底座上以4 m/s的初速度开始上升时刚好能到达顶端.求在环上升过程中底座对水平面的压力是多大?(g取10 m/s2)
例1.一汽车没有安装ABS,急刹车后,车轮在路面上滑动.(取g=10 m/s2)
⑴若车轮与干燥路面间的动摩擦因数是0.7 ,汽车以14m/s的速度在水平路面上行驶,急刹车后,滑行多远才停下?
⑵若车轮与湿滑路面间的动摩擦因数为0.1,在水平路面上汽车急刹车后的滑行距离不超过18m,刹车前的最大速度是多少?(14m;6m/s)
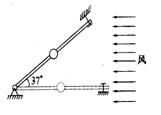 例2.如图所示,风洞实验室中可产生水平方向的、大小可调节的风力,现将一套有小球的细直杆放入风洞实验室,小球孔径略大于细杆直径.
例2.如图所示,风洞实验室中可产生水平方向的、大小可调节的风力,现将一套有小球的细直杆放入风洞实验室,小球孔径略大于细杆直径.
⑴当杆在水平方向上固定时,调节风力的大小,使小球在杆上做匀速运动,这时小球所受的风力为小球所受重力的0.5倍,求小球与杆间的动摩擦因数.
⑵保持小球所受风力不变,使杆与水平方向间夹角为37o并固定则小球从静止出发到在细杆上滑下距离x所需的时间为多少?
0.5;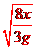 )
)
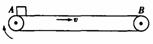
例3.水平传送带被广泛地应用于机场和火车站,如图所示为一水平传送带装置示意图.紧绷的传送带AB始终保持恒定的速率v=1 m/s运行,一质量为m=4kg的行李无初速度地放在A处,传送带对行李的滑动摩擦力使行李开始做匀加速直线运动,随后行李又以与传送带相等的速率做匀速直线运动.设行李与传送带之间的动摩擦因数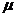 =0.1,A、B间的距离L=2m,g取10m/s2。
=0.1,A、B间的距离L=2m,g取10m/s2。
⑴求行李刚开始运动时所受滑动摩擦力的大小与加速度的大小;
 ⑵求行李做匀加速直线运动的时间;
⑵求行李做匀加速直线运动的时间;
⑶如果提高传送带的运行速率,行李就能被较快地传送到B处,求行李从A处传送到B处的最短时间和传送带对应的最小运行速率.
(1m/s2;1s;2 m/s、2s)
例4.如图所示,传送带与地面倾角θ=370,从A到B长度为16m,传送带以10 m/s的速度逆时针转动,在传送带上端A无初速地放一质量为0.5kg的物体,它与传送带之间的动摩擦因数为0.5,求物体从A运动到B所需的时间是多少?(t总=2 s)
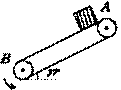
例5.固定光滑细杆与地面成一定倾角,在杆上套有一个光滑小环,小环在沿杆方向的推力F作用下向上运动,推力F与小环速度,随时间变化规律如图所示,取重力加速度g=10m/s2。 求:⑴小环的质量m;⑵细杆与地面间的倾角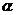 。
。
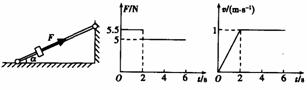
(1kg;30°)
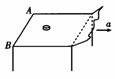 例6.一小圆盘静止在桌布上,位于一方桌的水平桌面的中央.桌布的一边与桌的AB 边重合,如图所示.已知盘与桌布间的动摩擦因数为
例6.一小圆盘静止在桌布上,位于一方桌的水平桌面的中央.桌布的一边与桌的AB 边重合,如图所示.已知盘与桌布间的动摩擦因数为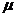 1,盘与桌面间的动摩擦因数为
1,盘与桌面间的动摩擦因数为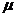 2.现突然以恒定加速度a将桌布抽离桌面,加速度方向是水平的且垂直于AB边.若圆盘最后未从桌面掉下,则加速度a满足的条件是什么?(以g表示重力加速度)
2.现突然以恒定加速度a将桌布抽离桌面,加速度方向是水平的且垂直于AB边.若圆盘最后未从桌面掉下,则加速度a满足的条件是什么?(以g表示重力加速度)
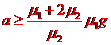
6.解方程,对解进行分析、检验或讨论。
[典题例析]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com