
8.已知函数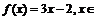 R.规定:给定一个实数x0,赋值
R.规定:给定一个实数x0,赋值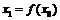 ,若
,若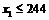 ,则继续赋值
,则继续赋值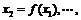 以此类推,若
以此类推,若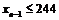 ,则
,则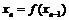 ,否则停止赋值,如果得到xn称为赋值了n次(n∈N*).已知赋值k次后该过程停止,则x0的取值范围是 ( )
,否则停止赋值,如果得到xn称为赋值了n次(n∈N*).已知赋值k次后该过程停止,则x0的取值范围是 ( )
A.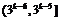 B.
B.
C. D.
D.
7.当a>0时,设命题P:函数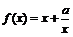 在区间(1,2)上单调递增;命题Q:不等式
在区间(1,2)上单调递增;命题Q:不等式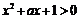 对任意x∈R都成立.若“P且Q”是真命题,则实数a的取
对任意x∈R都成立.若“P且Q”是真命题,则实数a的取 值范围是 ( )
值范围是 ( )
A.  B.
B.
C. 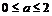 D.
D.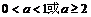
6. AB是某平面上一定线段,点P是该平面内的一动点,满足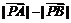 =2,|
=2,| |=
|=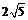 ,则点P的轨迹是 ( )
,则点P的轨迹是 ( )
A.圆 B.双曲线的一支 C.椭圆的一部分 D.抛物线
5.点P所在轨迹的极坐标方程为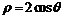 ,点Q所在轨迹的参数方程为在
,点Q所在轨迹的参数方程为在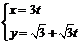 (t为参数)上,则|PQ|的最小值是 ( )
(t为参数)上,则|PQ|的最小值是 ( )
A.2 B.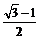 C.1 D.
C.1 D.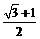
4.在对两个变量x、y进行线性回归分析时一般有下列步骤:
①对所求出的回归方程作出解释; ②收集数据
③求线性回归方程; ④求相关系数;
⑤根据所搜集的数据绘制散点图.
如果根据可靠性要求能够 判定变量x、y具有线性相关性,则在下列操作顺序中正确的是( )
判定变量x、y具有线性相关性,则在下列操作顺序中正确的是( )
A.①②⑤③④ B.③②④⑤① C.②④③①⑤ D.②⑤④③①
3.已知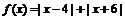 的最小值为n,则二项式
的最小值为n,则二项式 展开式中常数项是 ( )
展开式中常数项是 ( )
A.第7项 B.第8项 C.第9项 D.第10项
2. 某几何体的三视图如图所示,根据图中标出的数据,
某几何体的三视图如图所示,根据图中标出的数据,
可得这个几何体的表面积为 ( )
A. B.
B.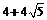
C.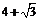 D.12
D.12
1.已知集合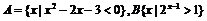 ,则A∩B= ( )
,则A∩B= ( )
A.{x| x>1} B.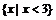 C.
C.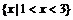 D.{
D.{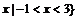
21.解析:(1)由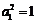 ,
, 得,
得,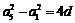 ,
,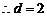 .
2分
.
2分
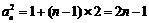 ,
, 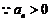 ,
, ,数列
,数列 的通项公式为
的通项公式为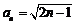 ; 4分
; 4分
(2)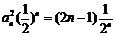 ,
,
设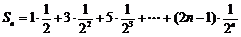 ①
5分
①
5分
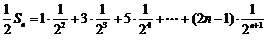 ②
6分
②
6分
①-②,得
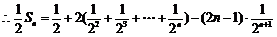

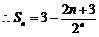 .
8分
.
8分
即数列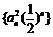 的前
的前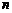 项和为
项和为 ;
;
(3)解法一: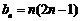 ,不等式
,不等式 恒成立,即
恒成立,即 对于一切的
对于一切的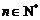 恒成立.
10分
恒成立.
10分
设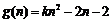 . 11分
. 11分
当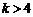 时,由于对称轴
时,由于对称轴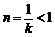 ,且
,且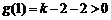
而函数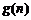 在
在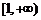 是增函数,
12分
是增函数,
12分
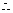 不等式
不等式 恒成立,
恒成立,
即当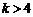 时,不等式
时,不等式 对于一切的
对于一切的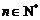 恒成立. 13分
恒成立. 13分
解法二: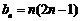 ,不等式
,不等式 恒成立,即
恒成立,即 对于一切的
对于一切的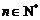 恒成立.
10分
恒成立.
10分
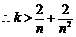 11分
11分
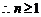 ,
,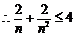 . 12分
. 12分
而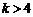
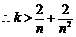 恒成立.
恒成立.
故当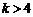 时,不等式
时,不等式 对于一切的
对于一切的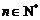 恒成立. 13分
恒成立. 13分
20. 解析:(1)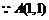 是椭圆
是椭圆 上的一点,
上的一点,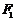 、
、 为两个焦点,
为两个焦点,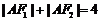 ,
,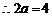 ,
,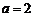 ,
2分
,
2分
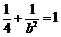 ,
,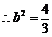 ,
, ,
4分
,
4分
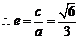 .椭圆的方程为
.椭圆的方程为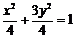 .
6分
.
6分
(2)设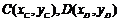 ,
,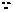 直线
直线 、
、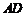 的倾斜角互补,
的倾斜角互补,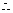 直线
直线 、
、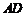 的斜率互为相反数,
的斜率互为相反数,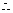 直线
直线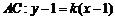 ,直线
,直线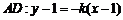 . 8分
. 8分
由 ,得
,得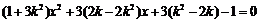 10分
10分
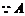 点的横坐标
点的横坐标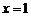 一定为该方程的解.
一定为该方程的解.
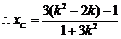 ,同理,
,同理,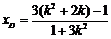 . 12分
. 12分
 .
.
故直线 的斜率为定值
的斜率为定值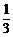 .
13分
.
13分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com