
5.与命题“若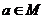 则
则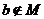 ”的等价的命题是( )
”的等价的命题是( )
A.若 ,则
,则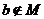 B.若
B.若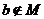 ,则
,则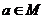
C.若 ,则
,则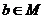 D.若
D.若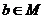 ,则
,则
4.若函数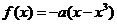 的递减区间为(
的递减区间为(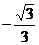 ,
,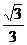 ),则a的取值范围是( )
),则a的取值范围是( )
A.a>0 B.-1<a<0
C.a>1 D.0<a<1
3.已知数列 前n项和为
前n项和为 ,则
,则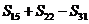 的值是( )
的值是( )
A.13 B.-76 C.46 D.76
2.(理)复数 ( )
( )
A. B.
B.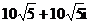
C.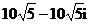 D.
D.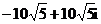
(文)点M(8,-10),按a平移后的对应点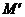 的坐标是(-7,4),则a=( )
的坐标是(-7,4),则a=( )
A.(1,-6) B.(-15,14)
C.(-15,-14) D.(15,-14)
1.(理)全集设为U,P、S、T均为U的子集,若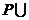 (
(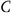
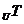 )=(
)=(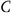
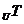 )
) 则( )
则( )
A. B.P=T=S
B.P=T=S
C.T=U D.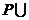
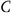
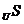 =T
=T
(文)设集合 ,
,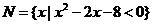 ,若U=R,且
,若U=R,且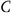
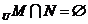 ,则实数m的取值范围是( )
,则实数m的取值范围是( )
A.m<2 B.m≥2
C.m≤2 D.m≤2或m≤-4
16.(1)由已知,设椭圆方程为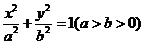 ,
,
由于焦点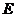 的坐标为
的坐标为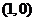 ,它对应的准线方程为
,它对应的准线方程为  ,…………………………2分
,…………………………2分
所以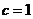 ,
,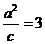 ,于是
,于是 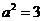 ,
,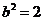 ,
,
所以所求的椭圆方程为: 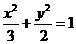 . ……………………………………………4分
. ……………………………………………4分
(2) 由题意可知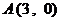 ,
,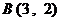 ,
,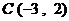 ,
,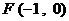 .
.
所以直线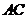 和直线
和直线 的方程分别为:
的方程分别为: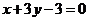 ,
, ,
,
由 解得
解得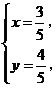 所以
所以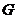 点的坐标为
点的坐标为 .………………6分
.………………6分
所以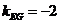 ,
, ,
,
因为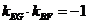 ,所以
,所以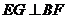 ,…………………………………………8分
,…………………………………………8分
所以⊙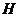 的圆心为
的圆心为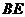 中点
中点 ,半径为
,半径为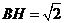 ,
,
所以⊙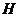 方程为
方程为  .………………………………………10分
.………………………………………10分
(3) 设 点的
点的 坐标为
坐标为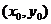 ,则
,则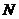 点的坐标为
点的坐标为 ,
,
因为点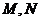 均在⊙
均在⊙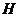 上,所以
上,所以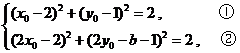 ,
,
由②-①×4,得 ,
,
所以点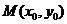 在直线
在直线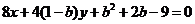 ,………………1
,………………1 2分
2分
又因为点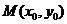 在⊙
在⊙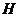 上,
上,
所以圆心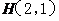 到直线
到直线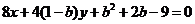 的距离
的距离

 ,………………………………14分
,………………………………14分
即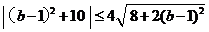 ,
,
整理,得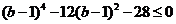 ,即
,即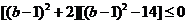 ,
,
 所以
所以 ,故
,故 的取值范围为
的取值范围为 .………16分
.………16分
解法二:过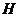 作
作 交
交 于
于 ,
,
设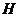 到直
到直 线
线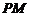 的距离
的距离
 ,则
,则
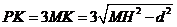 ,
,
 ,
,
又因为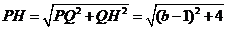
所以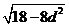
 ,
, ,因为
,因为 ,
,
所以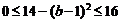 ,所以
,所以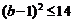 ,
, ;
;
解法三:因为 ,
,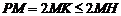 ,所以
,所以
所以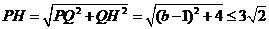 ,所以
,所以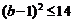 ,
, .
.
15.证明:⑴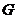 是
是 的交点,∴
的交点,∴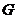 是
是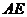 中点,又
中点,又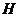 是
是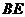 的中点,
的中点,
∴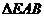 中,
中,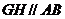 ,
------------------------3分
,
------------------------3分
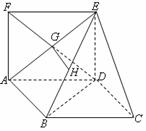

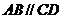 ,∴
,∴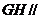
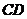 ,
,
又∵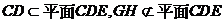
∴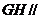 平面
平面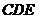 --------------7分
--------------7分
⑵平面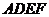
 平面
平面 ,交线为
,交线为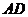 ,
,
∵ ,
,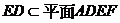
∴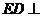 平面
平面 ,
----------------10分
,
----------------10分
∴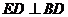 ,
,
又∵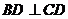 ,
,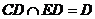
∴ ---------------------14分
---------------------14分
16.在矩形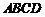 中,已知
中,已知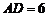 ,
,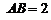 ,E、F为
,E、F为 的两个三等分点,
的两个三等分点,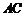 和
和 交于点
交于点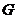 ,
, 的外接圆为⊙
的外接圆为⊙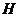 .以
.以 所在直线为
所在直线为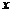 轴,以
轴,以 中点
中点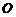 为坐标原点,建立如图所示的平面直角坐标系.
为坐标原点,建立如图所示的平面直角坐标系.
(1)求以F、E为焦点,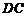 和
和 所在直线为准线的椭圆的方程;
所在直线为准线的椭圆的方程;
(2)求⊙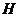 的方程;
的方程;
 (3)设点
(3)设点 ,过点P作直线与⊙
,过点P作直线与⊙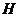 交于M,N两点,若点M恰好是线段PN的中点
交于M,N两点,若点M恰好是线段PN的中点 ,求实数
,求实数 的取值范围.
的取值范围.
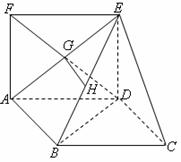
15.如图,平行四边形 中,
中,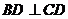 ,正方形
,正方形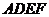 所在的平面和平面
所在的平面和平面 垂直,
垂直,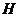 是
是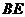 的中点,
的中点,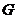 是
是 的交点.(1)求证:
的交点.(1)求证: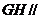 平面
平面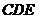 ;(2)求证:
;(2)求证: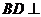 平面
平面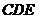 .
.
14.已知数列 的通项公式是
的通项公式是 ,数列
,数列 的通项公式是
的通项公式是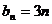 ,令集合
,令集合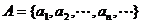 ,
, ,
, .将集合
.将集合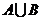 中的元素按从小到大的顺序排列构成的数列记为
中的元素按从小到大的顺序排列构成的数列记为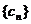 .则数列
.则数列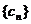 的前28项的和
的前28项的和 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com