
23.(石景山·文·题19)
已知椭圆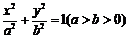 的离心率为
的离心率为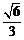 ,长轴长为
,长轴长为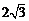 ,直线
,直线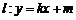 交椭圆于不同的两点
交椭圆于不同的两点 ,
, .
.
⑴求椭圆的方程;
⑵若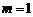 ,且
,且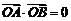 ,求
,求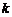 的值(
的值( 点为坐标原点);
点为坐标原点);
⑶若坐标原点 到直线
到直线 的距离为
的距离为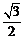 ,求
,求 面积的最大值.
面积的最大值.
[解析]
⑴设椭圆的半焦距为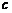 ,依题意
,依题意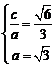 ,解得
,解得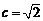 .
.
由 ,得
,得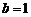
∴所求椭圆方程为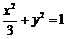
⑵∵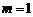 ,∴
,∴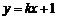 .
.
设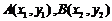 ,其坐标满足方程
,其坐标满足方程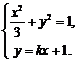 ,
,
消去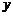 并整理得
并整理得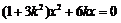 ,
,
则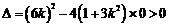 ,解得
,解得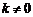
故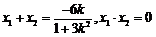 .
.
∵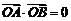 ,
,
∴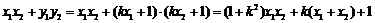
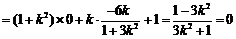
∴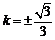 .
.
⑶由已知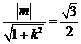 ,可得
,可得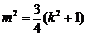 .
.
将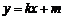 代入椭圆方程,整理得
代入椭圆方程,整理得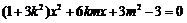
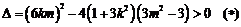
∴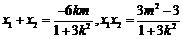
∴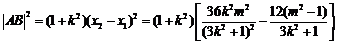
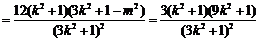
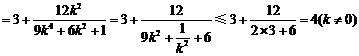 .
.
当且仅当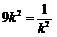 ,即
,即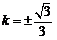 时等号成立.
时等号成立.
经检验,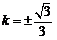 满足
满足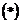 式.
式.
当 时,
时,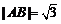
综上可知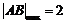
∴当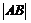 最大时,
最大时,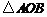 的面积取最大值
的面积取最大值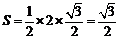 .
.
22.(石景山·理·题19)
已知椭圆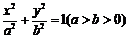 的离心率为
的离心率为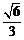 ,短轴的一个端点到右焦点的距离为
,短轴的一个端点到右焦点的距离为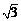 ,直线
,直线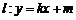 交椭圆于不同的两点
交椭圆于不同的两点 ,
, .
.
⑴求椭圆的方程;
⑵若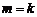 ,且
,且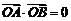 ,求
,求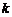 的值(
的值( 点为坐标原点);
点为坐标原点);
⑶若坐标原点 到直线
到直线 的距离为
的距离为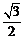 ,求
,求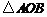 面积的最大值.
面积的最大值.
[解析]
⑴设椭圆的半焦距为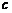 ,依题意
,依题意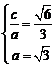 ,解得
,解得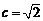 .
.
由 ,得
,得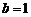
∴所求椭圆方程为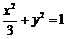
⑵∵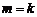 ,∴
,∴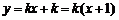 .
.
设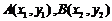 ,其坐标满足方程
,其坐标满足方程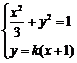 ,消去
,消去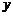 并整理得
并整理得
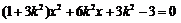 ,
,
则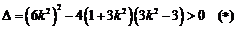
故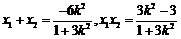 .
.
∵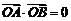 ,
,
∴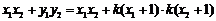
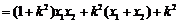
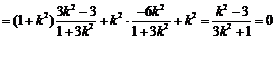
∴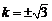 ,经检验
,经检验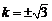 满足
满足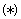 式.
式.
⑶由已知,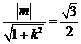 ,可得
,可得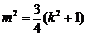
将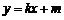 代入椭圆方程,整理得
代入椭圆方程,整理得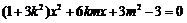
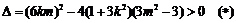
∴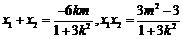 .
.
∴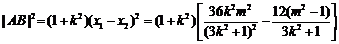
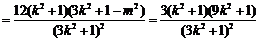
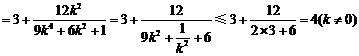
当且仅当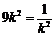 ,即
,即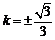 时等号成立.
时等号成立.
经检验,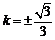 满足(*)式.
满足(*)式.
当 时,
时,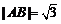
综上可知,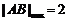
所以,当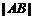 最大时,
最大时,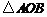 的面积取得最大值
的面积取得最大值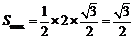 .
.
21.(丰台·文科·题19)
在直角坐标系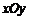 中,点
中,点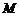 到点
到点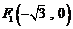 ,
,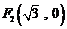 的距离之和是
的距离之和是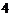 ,点
,点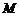 的轨迹是
的轨迹是 ,直线
,直线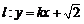 与轨迹
与轨迹 交于不同的两点
交于不同的两点 和
和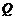 .
.
⑴求轨迹 的方程;
的方程;
⑵是否存在常数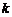 ,
,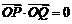 ?若存在,求出
?若存在,求出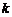 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
[解析]
⑴∵点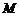 到
到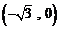 ,
,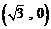 的距离之和是
的距离之和是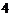 ,
,
∴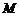 的轨迹
的轨迹 是长轴为
是长轴为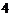 ,焦点在
,焦点在 轴上焦距为
轴上焦距为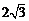 的椭圆,
的椭圆,
 其方程为
其方程为 .
.
⑵将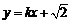 ,代入曲线
,代入曲线 的方程,
的方程,
整理得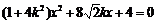 ①
①
设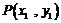 ,
,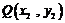 由方程①,得
由方程①,得
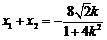 ,
,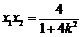 ②
②
又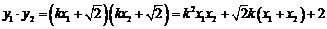 ③
③
若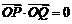 ,得
,得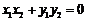
将②、③代入上式,解得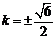 .
.
又因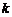 的取值应满足
的取值应满足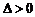 ,即
,即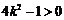 (*),
(*),
将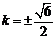 代入(*)式知符合题意.
代入(*)式知符合题意.
20.(丰台·理科·题19)
在直角坐标系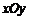 中,点
中,点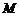 到点
到点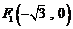 ,
,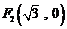 的距离之和是
的距离之和是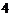 ,点
,点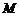 的轨迹是
的轨迹是 与
与 轴的负半轴交于点
轴的负半轴交于点 ,不过点
,不过点 的直线
的直线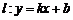 与轨迹
与轨迹 交于不同的两点
交于不同的两点 和
和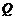 .
.
⑴求轨迹 的方程;
的方程;
⑵当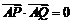 时,求
时,求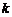 与
与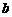 的关系,并证明直线
的关系,并证明直线 过定点.
过定点.
[解析]
⑴∵点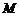 到
到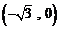 ,
,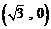 的距离之和是
的距离之和是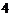 ,
,
∴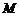 的轨迹
的轨迹 是长轴为
是长轴为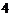 ,焦点在
,焦点在 轴上焦中为
轴上焦中为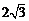 的椭圆,
的椭圆,
其方程为 .
.

⑵将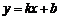 ,代入曲线
,代入曲线 的方程,整理得
的方程,整理得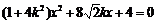
因为直线 与曲线
与曲线 交于不同的两点
交于不同的两点 和
和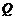 ,
,
所以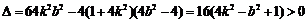 ①
①
设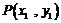 ,
,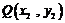 ,则
,则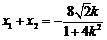 ,
,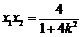 ②
②
且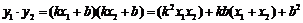
显然,曲线 与
与 轴的负半轴交于点
轴的负半轴交于点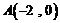 ,
,
所以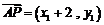 ,
,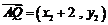 .
.
由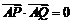 ,得
,得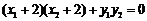 .
.
将②、③代入上式,整理得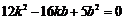 .
.
所以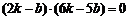 ,即
,即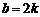 或
或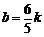 .经检验,都符合条件①
.经检验,都符合条件①
当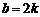 时,直线
时,直线 的方程为
的方程为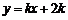 .
.
显然,此时直线 经过定点
经过定点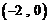 点.
点.
即直线 经过点
经过点 ,与题意不符.
,与题意不符.
当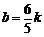 时,直线
时,直线 的方程为
的方程为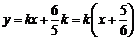 .
.
显然,此时直线 经过定点
经过定点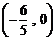 点,且不过点
点,且不过点 .
.
综上,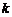 与
与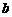 的关系是:
的关系是: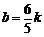 ,且直线
,且直线 经过定点
经过定点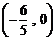 点.
点.
19.(海淀·文科·题19)
已知椭圆 的对称中心为原点
的对称中心为原点 ,焦点在
,焦点在 轴上,离心率为
轴上,离心率为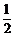 ,且点
,且点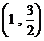 0在该椭圆上.
0在该椭圆上.
⑴求椭圆 的方程;
的方程;
⑵过椭圆 的左焦点
的左焦点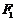 的直线
的直线 与椭圆
与椭圆 相交于
相交于 、
、 两点,若
两点,若 的面积为
的面积为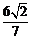 ,求圆心在原点
,求圆心在原点 且与直线
且与直线 相
相 切的圆的方程.
切的圆的方程.
[解析]
⑴设椭圆C的方程为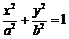
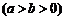 ,
,
由题意可得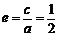 ,又
,又 ,所以
,所以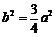
因为椭圆 经过
经过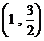 ,代入椭圆方程有
,代入椭圆方程有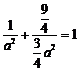 ,解得
,解得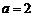
所以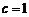 ,
,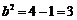 故椭圆
故椭圆 的方程为
的方程为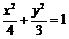 .
.
⑵解法一:
当直线
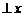 轴时,计算得到:
轴时,计算得到: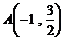 ,
,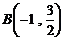 ,
,
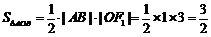 ,不符合题意.
,不符合题意.
当直线 与
与 轴不垂直时,设直线
轴不垂直时,设直线 的方程为:
的方程为: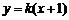 ,
,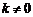
由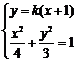 ,消去
,消去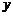 ,得
,得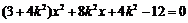
显然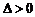 成立,设
成立,设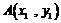 ,
,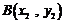 ,
,
则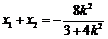 ,
,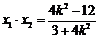
又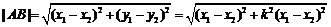
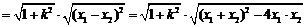

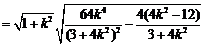
即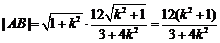
又圆 的半径
的半径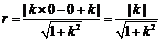
所以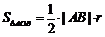
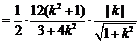
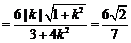
化简,得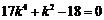 ,即
,即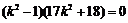 ,
,
解得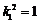 ,
,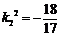 (舍)
(舍)
所以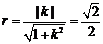 ,故圆
,故圆 的方程为
的方程为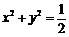 .
.
⑵解法二:
设直线 的方程为
的方程为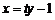 ,
,
由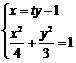 ,消去
,消去 ,得
,得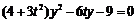
因为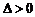 恒成立,设
恒成立,设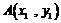 ,
,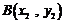 ,
,
则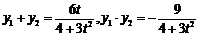
所以
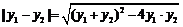
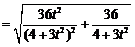
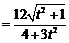
所以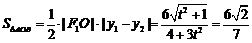
化简得到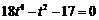 ,即
,即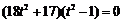 ,
,
解得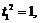
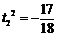 (舍)
(舍)
又圆 的半径为
的半径为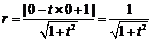
所以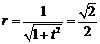 ,故圆
,故圆 的方程为:
的方程为: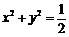
18.(海淀·理科·题19)
已知椭圆 的中心在原点,焦点在
的中心在原点,焦点在 轴上,左右焦点分别为
轴上,左右焦点分别为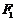 ,
,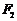 ,且
,且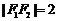 ,点
,点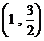 在椭圆
在椭圆 上.
上.
⑴求椭圆 的方程;
的方程;
⑵过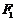 的直线
的直线 与椭圆
与椭圆 相交于
相交于 、
、 两点,且
两点,且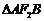 的面积为
的面积为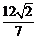 ,求以
,求以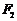 为圆心且与直线
为圆心且与直线 相切的圆的方程.
相切的圆的方程.
[解析]
⑴设椭圆的方程为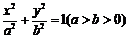 ,由题意可得:
,由题意可得:
椭圆 两焦点坐标分别为
两焦点坐标分别为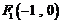 ,
,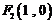 .
.
∴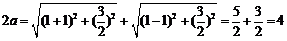 .
.
∴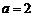 ,又
,又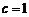 ,
,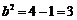 ,
,
故椭圆的方程为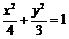 .
.
⑵当直线
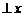 轴,计算得到:
轴,计算得到: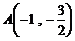 ,
,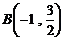 ,
,
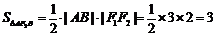 ,不符合题意.
,不符合题意.
当直线 与
与 轴不垂直时,设直线
轴不垂直时,设直线 的方程为:
的方程为: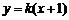 ,
,
由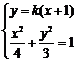 ,消去y得
,消去y得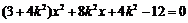 .
.
显然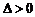 成立,设
成立,设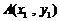 ,
,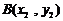 ,
,
则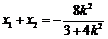 ,
,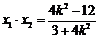 .
.
又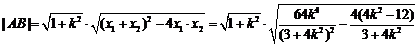
即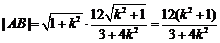 ,
,
又圆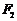 的半径
的半径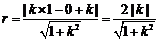 .
.
所以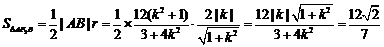 ,
,
化简,得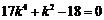 ,即
,即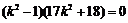 ,解得
,解得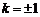 .
.
所以,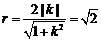 .
.
故圆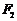 的方程为:
的方程为: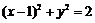 .
.
⑵另解:设直线 的方程为
的方程为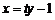 ,
,
由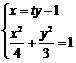 ,消去
,消去 得
得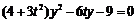 ,
,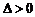 恒成立,
恒成立,
设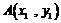 ,
,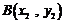 ,则
,则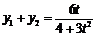 ,
,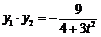 .
.
所以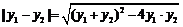
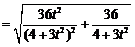
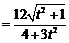 .
.
又圆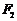 的半径为
的半径为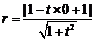
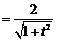 .
.
所以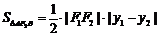
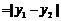
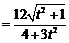
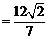 ,解得
,解得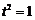 ,
,
所以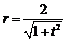
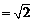 .
.
故圆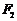 的方程为:
的方程为: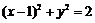 .
.
17.(朝阳·文·题10)
在抛物线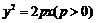 上,横坐标为4的点
上,横坐标为4的点 到焦点的距离为5,则
到焦点的距离为5,则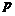
 的值为 .
的值为 .
[解析] 2;
由抛物线的几何性质,有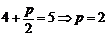 .
.
16.(朝阳·理·题10)(朝阳·文·题13)
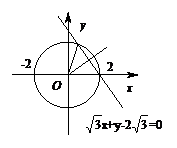
圆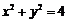 被直
被直 线
线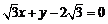 截得的劣弧所对的圆心角的大小为 .
截得的劣弧所对的圆心角的大小为 .
[解析]
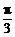 .
.
圆心到直线的距离为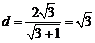 .不妨设劣弧所对的圆心角为
.不妨设劣弧所对的圆心角为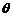 ,于是
,于是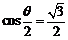 .解得
.解得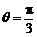 .
.
15.(朝阳·理·题6)
已知点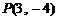 是双曲线
是双曲线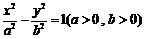 渐近线上的一点,
渐近线上的一点,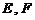 是左、右两个焦点,若
是左、右两个焦点,若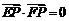 ,则双曲线方程为( )
,则双曲线方程为( )
A.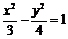 B.
B.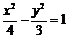 C.
C.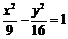 D.
D.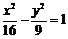
[解析] C;
不妨设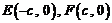 ,于是有
,于是有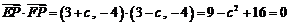 .
.
于是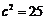 .排除A,B.又由D中双曲线的渐近线方程为
.排除A,B.又由D中双曲线的渐近线方程为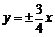 ,点
,点 不在其上.排除D.
不在其上.排除D.
14.(崇文·文·题4)
若直线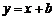 与圆
与圆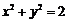 相切,则
相切,则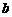 的值为 ( )
的值为 ( )
A.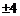 B.
B.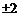 C.
C.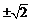 D.
D.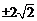
[解析] B;
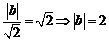 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com