
21、(12分)已知数列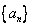 的前n项和
的前n项和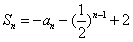 (n为正整数)。
(n为正整数)。
(Ⅰ)令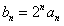 ,求证数列
,求证数列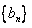 是等差数列,并求数列
是等差数列,并求数列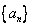 的通项公式;
的通项公式;
(Ⅱ)令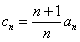 ,
,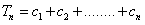 ,
,
若对于任意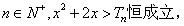 求实数
求实数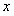 的取值集合。
的取值集合。
20.(12分)已知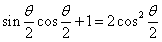 ,其中
,其中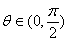
(1)求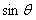 和
和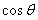 的值
的值
(2)若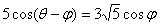 ,
,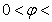
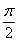 ,求
,求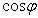 的值
的值
19.(12分)已知点(1,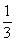 )是函数
)是函数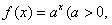 且
且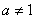 )的图象上一点,
)的图象上一点,
等比数列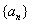 的前
的前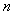 项和为
项和为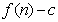 ,数列
,数列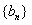
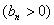 的首项为
的首项为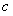 ,且前
,且前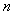 项和
项和
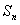 满足
满足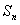 -
-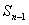 =
=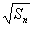 +
+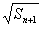 (
(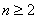 ).
).
(1)求数列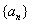 和
和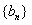 的通项公式;
的通项公式;
(2)若数列{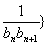 前
前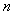 项和为
项和为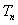 ,问
,问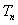 >
>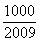 的最小正整数
的最小正整数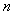 是多少?
是多少?
18.(12分)已知定义域为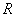 的函数
的函数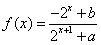 是奇函数。
是奇函数。
(Ⅰ)求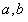 的值;
的值;
(Ⅱ)若对任意的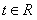 ,不等式
,不等式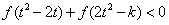 恒成立,求
恒成立,求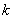 的取值范围;
的取值范围;
(注意:在试题卷上作答无效)
17.(10分)已知 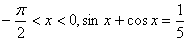 .
.
(I)求sinx-cosx的值;
(Ⅱ)求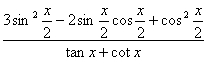 的值.
的值.
16.下列命题中,正确命题的序号是
①函数
②函数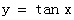 在定义域内是增函数。
在定义域内是增函数。
③函数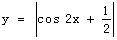 的周期是
的周期是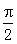 。
。
④函数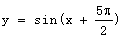 是偶函数。
是偶函数。
⑤函数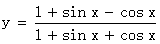 是奇函数。
是奇函数。
15.设非零向量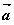 、
、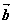 、
、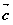 满足
满足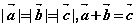 ,则
,则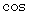
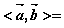
14.已知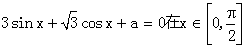 内有两相异实根
内有两相异实根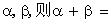
(注意:在试题卷上作答无效)
13.设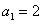 ,
,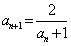 ,
,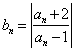 ,
,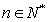 ,则数列
,则数列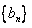 的通项公式
的通项公式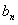 =
.
=
.
12.定义在R上的函数f(x)满足f(x)= 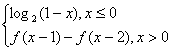 ,则f(2010)的值为( )
,则f(2010)的值为( )
A.-1 B. 0 C.1 D. 2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com