
2.设集合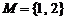 ,则满足条件
,则满足条件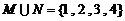 的集合
的集合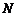 的个数是 ( )
的个数是 ( )
A. B.
B.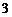 C.
C. D.
D.
1.集合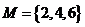 的真子集的个数为 ( )
的真子集的个数为 ( )
A.6 B.7 C.8 D.9
例1.(广东省惠州市2008)设集合 ,则满足
,则满足 的集合B的个数是
的集合B的个数是
( )
A.1 B.3 C.4 D.8
例2.(江苏省启东中学2008)定义集合A*B={x|xA,且x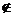 B},若A={1,3,5,7},B={2,3,5},则A*B的子集个数为 ( )
B},若A={1,3,5,7},B={2,3,5},则A*B的子集个数为 ( )
A.1 B.2 C.3 D.4
例3.(2008年金华一中)定义
 ,设
,设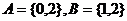 ,则
,则 中所有元素和为 ( )
中所有元素和为 ( )
A.1 B.3 C.9 D.18
例4.(2008年山东卷,数学文科理科,1)满足M {a1, a2, a3, a4},且M∩{a1 ,a2, a3}={ a1·a2}的集合M的个数是 ( )
{a1, a2, a3, a4},且M∩{a1 ,a2, a3}={ a1·a2}的集合M的个数是 ( )
A.1 B.2 C.3 D.4
例5.若集合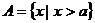 ,
,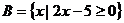 ,且满足
,且满足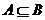 ,求实数
,求实数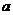 的取值范围.
的取值范围.
例6.已知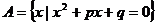 ,集合
,集合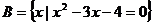 ,且满足
,且满足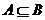 ,求实数p,q满足的条件.
,求实数p,q满足的条件.
2、注意特殊集合空集,空集是任何集合的子集,在解型如A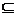 B类题时,要首先考虑集合A为空集时,并且有A=B或A≠B两种可能,注意应用分类讨论的思想。
B类题时,要首先考虑集合A为空集时,并且有A=B或A≠B两种可能,注意应用分类讨论的思想。
1、解答集合问题,首先要正确理解集合的有关概念,特别是集合中元素的三个特征;对于用描述法给出的集合,要先看集合中的代表元素是谁,以及它所具有的性质;要重视发挥图示法的作用,通过数形结合直观地解决问题
3、两个特殊的集合:
(1)空集:
.记作:

(2)全集:
.记作:

2、两类关系:
(1)元素与集合的关系,用
或 表示;
(2)集合与集合的关系,用
,
, 表示,
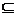
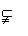 当A
B时,称A是B的
;
当A
B时,称A是B的
;
当A
B时,称A是B的
.
1、集合的概念:
(1)集合中元素特征:
,
,

(2)集合的分类:
①按元素个数分:
,
;
②按元素特征分:
,

举例说明:
(3)集合的表示法: ;

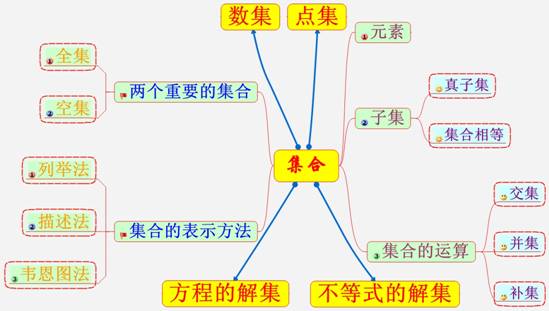

请同学们对照知识导图,回顾本章的基础知识.
3、情感.态度与价值观
学习集合后要有所收获,增强学好数学的自信心.
[学习重点]: 复习集合的表示方法和集合关系. 
[学习难点]:子集的包含关系和子集的个数.
[学习教具]:多媒体
[学习方法]:自主整理、回顾复习.
[学习过程]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com