
9. 已知双曲线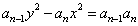 的焦点在y轴上,一条渐近线方程为
的焦点在y轴上,一条渐近线方程为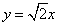 ,其中
,其中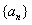 是以 4 为首项的正数数列,则数列
是以 4 为首项的正数数列,则数列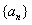 的通项公式是( )
的通项公式是( )
A.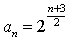 B.
B.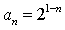 C.
C.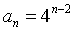 D.
D.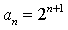
8.已知定义在R上的函数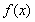 为奇函数,且函数
为奇函数,且函数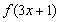 的周期为3,且
的周期为3,且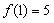 ,则
,则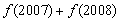 的值为( )
的值为( )
A.0 B.5 C.2 D.– 5
7.将函数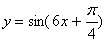 的图像上各点的横坐标伸长到原来的3倍,再向右平移
的图像上各点的横坐标伸长到原来的3倍,再向右平移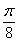 个单位,得到的函数的一个对称中心是(
)
个单位,得到的函数的一个对称中心是(
)
A.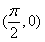
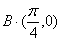 C.
C. 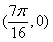 D.
D. 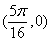
6.已知向量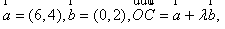 若点C在函数
若点C在函数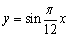 的图象上,则实数
的图象上,则实数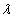 的值为(
)
的值为(
)
 A.
A.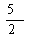 B.
B.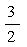 C.
C.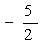 D.
D.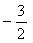
5. 已知函数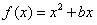 的图像在点
的图像在点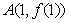 处切线的斜率为3,数列
处切线的斜率为3,数列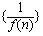 的前n项和为
的前n项和为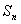 ,则
,则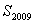 的值为 ( )
的值为 ( )
A.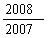 B.
B. 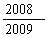 C.
C. 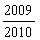 D.
D.
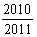
4.已知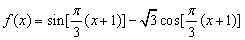 ,则
,则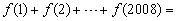 (
)
(
)
A.2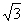 B.
B.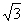 C.1 D.0
C.1 D.0
3. 函数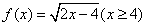 的反函数为( )
的反函数为( )
A.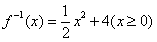 B.
B.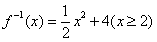
C.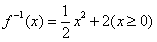 D.
D.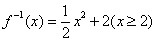
2. 若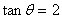 ,则
,则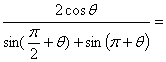 ( )
( )
A.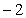 B.
B. 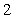 C.
C.
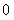 D.
D. 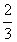
1.集合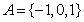 ,
,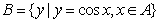 ,则
,则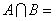 ( )
( )
A.{0} B.{1} C.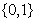 D.
D.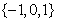
(17) ( 本题满分12分 )
已知函数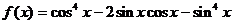
(I)求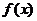 的最小正周期;
的最小正周期;
(II)若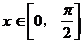 ,求
,求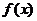 的最大值,最小值.
的最大值,最小值.
(18) ( 本题满分12分 )
已知一台机器在一天内发生故障的概率为0.2,机器发生故障时全天停止工作.一周五天工作日里无故障可获利10万元,发生一次故障可获利5万元,发生两次故障没有利润,发生三次或三次以上故障就要亏损2万元.这台机器在一周内平均获利多少?
(19) ( 本题满分12分 )
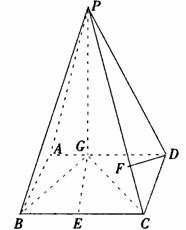 已知,如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上,且AG=
已知,如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上,且AG=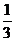 GD,BG⊥GC,GB=GC=2,E是BC的中点,四面体P-BCG的体积为
GD,BG⊥GC,GB=GC=2,E是BC的中点,四面体P-BCG的体积为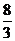 .
.
(Ⅰ)求异面直线GE与PC所成的角;
(Ⅱ)求点D到平面PBG的距离;
(Ⅲ)若F点是棱PC上一点,且DF⊥GC,求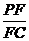 的值.
的值.
(20) ( 本题满分12分 )
已知等差数列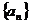 的前n 项之和为Sn,令
的前n 项之和为Sn,令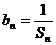 ,且
,且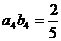 ,S6-S3=15.
,S6-S3=15.
(Ⅰ)求数列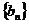 的通项公式与它的前10项之和;
的通项公式与它的前10项之和;
(Ⅱ)若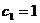 ,
,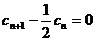 ,
,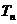 =
=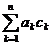 ,求
,求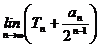 的值.
的值.
(21) ( 本题满分12分 )
已知点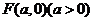 ,动点
,动点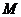 、
、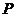 分别在
分别在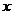 、
、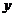 轴上运动,满足
轴上运动,满足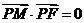 ,
,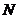 为动点,并且满足
为动点,并且满足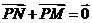 .
.
(Ⅰ)求点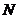 的轨迹
的轨迹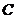 的方程;
的方程;
(Ⅱ)过点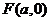 的直线
的直线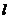 (不与
(不与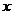 轴垂直)与曲线
轴垂直)与曲线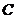 交于
交于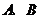 两点,设点
两点,设点 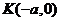 ,
,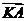 与
与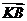 的夹角为
的夹角为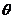 ,求证:
,求证: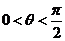 .
.
(22) ( 本题满分14分 )
函数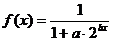 的定义域为R,且
的定义域为R,且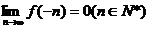
(Ⅰ)求证: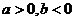 ;
;
(Ⅱ)若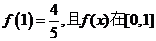 上的最小值为
上的最小值为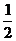 ,试求f(x)的解析式;
,试求f(x)的解析式;
(Ⅲ)在(Ⅱ)的条件下记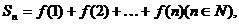 试比较
试比较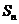 与
与
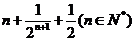 的大小并证明你的结论.
的大小并证明你的结论.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com