
4.右面算法输出的结果是 。
2.已知向量a和向量b的夹角为120°,|a|=3,|b|=5,则|a-b|= 。
 3.若
3.若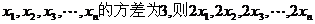 的方差为 。
的方差为 。
1.若复数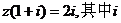 是虚数单位,则复数z= 。
是虚数单位,则复数z= 。
23.(本题满分18分,第(1)题5分,第(2)题8分,第(3)题5分)
设函数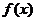 的定义域为
的定义域为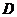 ,值域为
,值域为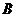 ,如果存在函数
,如果存在函数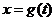 ,使得函数
,使得函数 的值域仍然是
的值域仍然是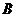 ,那么,称函数
,那么,称函数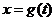 是函数
是函数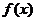 的一个等值域变换,
的一个等值域变换,
(1)判断下列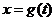 是不是
是不是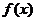 的一个等值域变换?说明你的理由;
的一个等值域变换?说明你的理由;
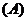
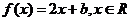 ,
,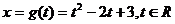 ;
;
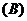
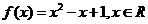 ,
,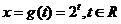 ;
;
(2)设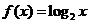 的值域
的值域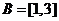 ,已知
,已知 是
是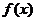 的一个等值域变换,且函数
的一个等值域变换,且函数 的定义域为
的定义域为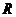 ,求实数
,求实数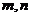 的值;
的值;
(3)设函数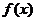 的定义域为
的定义域为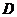 ,值域为
,值域为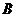 ,函数
,函数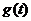 的定义域为
的定义域为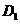 ,值域为
,值域为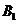 ,写出
,写出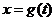 是
是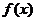 的一个等值域变换的充分非必要条件(不必证明),并举例说明条件的不必要性.
的一个等值域变换的充分非必要条件(不必证明),并举例说明条件的不必要性.
22.(本题满分16分,其中第(1)小题4分,第(2)小题8分,第(3)小题4分)
设 是两个数列,
是两个数列, 为直角坐标平面上的点.对
为直角坐标平面上的点.对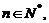 若三点
若三点 共线,
共线,
(1)求数列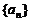 的通项公式;
的通项公式;
(2)若数列{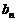 }满足:
}满足: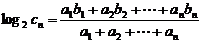 ,其中
,其中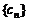 是第三项为8,公比为4的等比数列.求证:点列
是第三项为8,公比为4的等比数列.求证:点列 (1,
(1,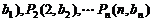 在同一条直线上;
在同一条直线上;
(3)记数列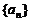 、{
、{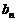 }的前
}的前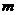 项和分别为
项和分别为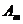 和
和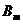 ,对任意自然数
,对任意自然数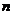 ,是否总存在与
,是否总存在与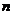 相关的自然数
相关的自然数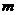 ,使得
,使得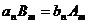 ?若存在,求出
?若存在,求出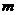 与
与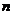 的关系,若不存在,请说明理由.
的关系,若不存在,请说明理由.
21.(本题16分,其中第(1)小题8分,第(2)小题8分)
已知椭圆 的方程为
的方程为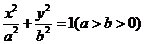 ,长轴是短轴的2倍,且椭圆
,长轴是短轴的2倍,且椭圆 过点
过点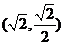 ;斜率为
;斜率为 的直线
的直线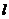 过点
过点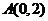 ,
, 为直线
为直线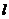 的一个法向量,坐标平面上的点
的一个法向量,坐标平面上的点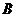 满足条件
满足条件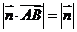 .
.
(1)写出椭圆 方程,并求点
方程,并求点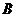 到直线
到直线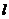 的距离;
的距离;
(2)若椭圆 上恰好存在3个这样的点
上恰好存在3个这样的点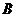 ,求
,求 的值.
的值.
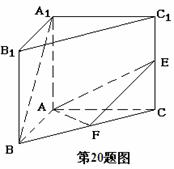
20.(本题14分,其中第(1)小题6分,第(2)小题8分)
设在直三棱柱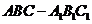 中,
中,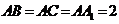 ,
,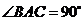 ,
, 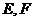 依次为
依次为 的中点.
的中点.
(1)求异面直线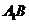 、
、 所成角
所成角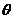 的大小(用反三角函数值表示);
的大小(用反三角函数值表示);
(2)求点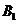 到平面
到平面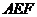 的距离.
的距离.
19.(本题14分,其中第(1)小题8分,第(2)小题6分)
如图所示,在一条海防警戒线上的点 、
、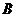 、
、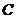 处各有一个水声监测点,
处各有一个水声监测点,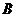 、
、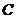 两点到点
两点到点 的距离分别为
的距离分别为 千米和
千米和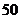 千米.某时刻,
千米.某时刻,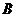 收到发自静止目标
收到发自静止目标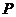 的一个声波信号,8秒后
的一个声波信号,8秒后 、
、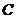 两点同时接收到该声波信号,已知声波在水中的传播速度是
两点同时接收到该声波信号,已知声波在水中的传播速度是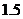 千米/秒.
千米/秒.
(1)设 到
到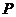 的距离为
的距离为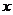 千米,用
千米,用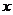 表示
表示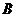 、
、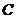 到
到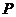 的距离,并求
的距离,并求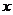 的值;
的值;
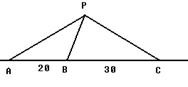 (2)求
(2)求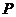 到海防警戒线
到海防警戒线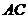 的距离(结果精确到
的距离(结果精确到 千米).
千米).
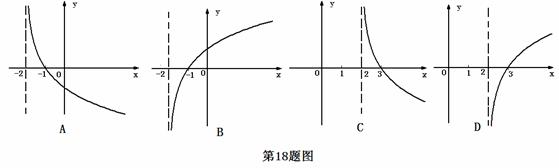
18.若函数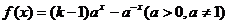 在
在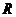 上既是奇函数,又是减函数,则
上既是奇函数,又是减函数,则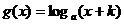 的图像是
的图像是
17. 已知集合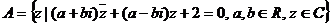 ,
,
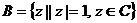 ,若
,若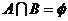 ,则
,则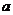 、
、 之间的关系是
之间的关系是
 .
.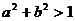
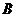 .
.
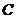 .
.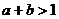
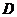 .
.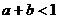
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com