读以极点为中心的经纬网图，图中的圆圈为赤道。据图中信息回答1-2题。

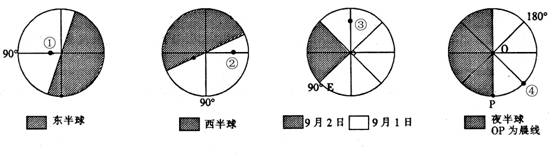
北京时间1999年10月 17日6时零 2分，一艘南驶的中国“盛鲁号”滚装轮，满载着旅客和船员出发，在离港3小时后突然失火，23分钟后停止在38°28′N，121°34′E的海域上。“SOS”呼救信号紧急发出；来救援船只在大火中展开了紧张的营救工作。据此回答3-5题。

1．启航时的港口可能是

A.大连　　　 　　　　　　　　　 B.秦皇岛　　 　　　　　　　　　　 C.烟台　　　 　　　　　　　　　　 D.青岛

2．从气象条件考虑，营救船只最好位于该船的

A.西北　 　　　　　　　　　　　　 B.东北　 　　　　　　　　　　　　　　 C.西南　 　　　　　　　　　　　　　　 D.东南

3．“盛鲁号”启航时，下列现象可信的是

A.南极长城站开始出现极昼现象　　 　 B. 澳大利亚墨累一达令盆地正值小麦播种季节

C.青海湖鸟岛正值观鸟的最佳时机　 D. 巴西巴西利亚此时东南日出、西南日落

　过一点作圆　　

　 过二点作圆　

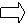
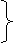
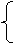
　　　　　 　　　　　三角形的外心　　　　　　　　 会用尺规作

　 过三点作圆　　 三角形的外接圆　　　 　　　　　　三角形的外

　　　　　　　 圆的内接三角形　　　　　　　　　 接圆

经过4个(或4个以上的)点是不是一定能作圆？

2. 判断：

(1)经过三个点一定可以作圆；(　　 )

(2)任意一个三角形一定有一个外接圆，并且只有一个外接圆；(　　　 )

(3)任意一个圆一定有一个内接三角形，并且只有一个内接三角形；(　　 )　　

(4)三角形的外心到三角形各顶点的距离都相等.(　　　 )

(5)三角形的外心是三角形三边的垂直平分线的交点. (　　 )

1. 按图填空：　　　　　　　　　　　

(1)△ABC是⊙O的　　　　 三角形；　　　　

(2)⊙O是△ABC的　　　 圆.　　　　　　　　　　　　　

5. 过同一直线上的三个点能不能作圆呢？(引导学生思考与尝试)

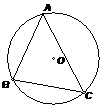　　　　　 学生得出：过同一直线上的三个点不能作圆

4. 介绍“三角形的外接圆”和“圆的内接三角形”以及“外心”的概念.

3.定理：不在同一直线上的三个点确定一个圆.

强调：(1)过同一直线上三点不行.

(2)“确定”一词应理解成“有且只有”.

2. 例：作圆，使它经过不在同一直线上的三个已知点.

已知：不在同一直线上的三点A、B、C(如图)

求作：⊙O，使它经过点A、B、C.

分析：

以前我们学过三角形两边垂直平分线的交点到三角形三个顶点的距离相等，若把三个已知点看作是三角形的三个顶点构造三角形，那么，两边垂直平分线的交点就是我们要找的圆心.

师生共同完成作图过程.(板书过程)

(结合以上的作法与证明，请学生回答下列问题，引出定理)

　　 ①、经过不在同一条直线上的三点A、B、C的圆是否承在？(承在)

　　 ②、是否还有其他符合条件的圆？(没有)

③根据是什么？(线段AB、BC的垂直平分线有且只有一个交点)

这说明所作的圆心是唯一的，从而半径也是唯一的，则所作的圆是唯一的.