
19.(本题满分14分)
解析:(Ⅰ)分数在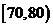 内的频率为:
内的频率为:
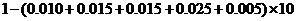
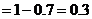 ,故
,故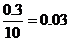 ,
,
如图所示: -----------------------4分
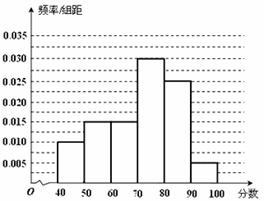 (求频率2分,作图2分)
(求频率2分,作图2分)
(Ⅱ)平均分为:
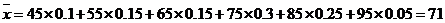 .----------------7分
.----------------7分
(Ⅲ)由题意,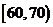 分数段的人数为:
分数段的人数为: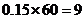 人;
人;
----------------8分
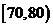 分数段的人数为:
分数段的人数为: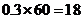 人;
人;
----------------9分
∵在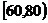 的学生中抽取一个容量为
的学生中抽取一个容量为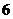 的样本,
的样本,
∴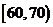 分数段抽取2人,分别记为
分数段抽取2人,分别记为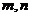 ;
;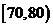 分数段抽取4人,分别记为
分数段抽取4人,分别记为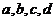 ;
;
设从样本中任取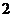 人,至多有1人在分数段
人,至多有1人在分数段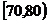 为事件
为事件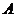 ,则基本事件空间包含的基本事件有:
,则基本事件空间包含的基本事件有:
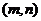 、
、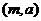 、
、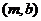 、
、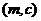 、
、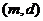 、……、
、……、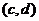 共15种,
共15种,
则事件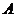 包含的基本事件有:
包含的基本事件有:
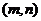 、
、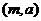 、
、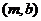 、
、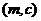 、
、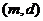 、
、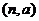 、
、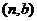 、
、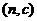 、
、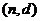 共9种,---
共9种,---
--
12分
∴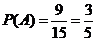 .
.
----------- ---------------------14分
---------------------14分
18.解:(1)
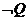 :
: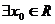 ,
,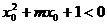 ……………(2分)
……………(2分)
若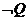 为真命题,则
为真命题,则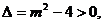 解得:
解得: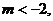 或
或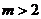
故所求实数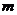 的取值范围为:
的取值范围为: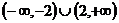 …………(5分)
…………(5分)
(2)若函数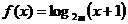 是增函数,则
是增函数,则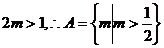 (7分)
(7分)
又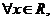
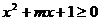 为真命题时,由
为真命题时,由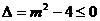
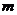 的取值范围为
的取值范围为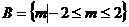 …………(9分)
…………(9分)
由“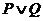 ” 为真命题,“
” 为真命题,“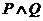 ”为假命题,故命题
”为假命题,故命题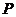 、
、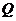 中有且仅有一个真命题
中有且仅有一个真命题
当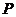 真
真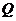 假时,实数
假时,实数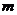 的取值范围为:
的取值范围为:
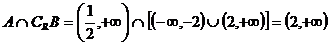 …………(11分)
…………(11分)
当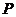 假
假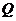 真时,实数
真时,实数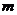 的取值范围为:
的取值范围为:
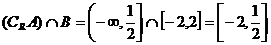 ………(13分)
………(13分)
综上可知实数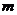 的取值范围:
的取值范围: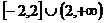 …………(14分)
…………(14分)
17.(1)证明:由已知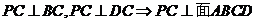 ……2分
……2分
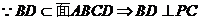 ,
,
又因为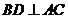 ,
, 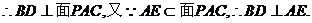 ……6分
……6分
(2)解:以正方形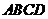 为底面,
为底面,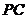 为高补成长方体,此时对角线
为高补成长方体,此时对角线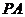 的长为球的直径,
的长为球的直径,
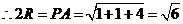 ,
,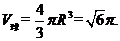 .
…12分
.
…12分
16.解:(Ⅰ)由图象知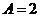
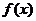 的最小正周期
的最小正周期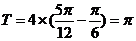 ,故
,故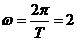 ……3分
……3分
将点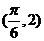 代入
代入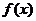 的解析式得
的解析式得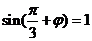 ,又
,又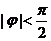 , ∴
, ∴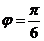
故函数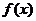 的解析式为
的解析式为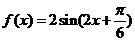 ……6分
……6分
(Ⅱ)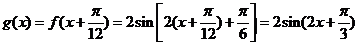 ……8分
……8分
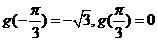
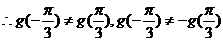 ……10分
……10分
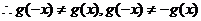 ,
,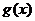 为非奇非偶函数. ……12分
为非奇非偶函数. ……12分
11 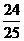 ; 12 127 ;13.
; 12 127 ;13.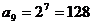 . 14
. 14 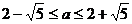 ; 15 90° .
; 15 90° .
21.(本小题满分l4分)
已知数列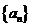 中,
中,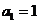 ,
,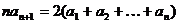
(1)求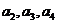 ;
;
(2)求数列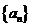 的通项
的通项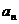 ;
;
(3)设数列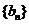 满足
满足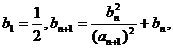 证明:①(
证明:①(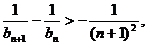 ;
②
;
②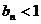 .
.
2010届高三数 学 (文科)2010.5
20.(本小题满分14分)
已知椭圆C: 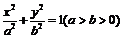 的离心率为
的离心率为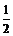 ,B,F分别是它的上顶点和右焦点.椭圆C上的点到点F的最短距离为2.圆M是过点B,F的所有圆中面积最小的圆.
,B,F分别是它的上顶点和右焦点.椭圆C上的点到点F的最短距离为2.圆M是过点B,F的所有圆中面积最小的圆.
(1)求椭圆C和圆M的方程;
(2)从圆外一点P引圆M的切线PQ,切点为Q,且有|PQ|=|PO|,O是坐标原点,求|PF|的最小值.
19.(本小题满分14分)
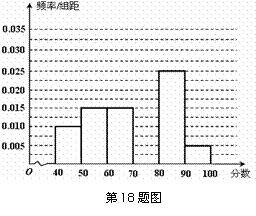 某校从参加高一年级期中考试的学生中随机抽取
某校从参加高一年级期中考试的学生中随机抽取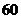 名学生,将其数学成绩(均为整数)分成六段
名学生,将其数学成绩(均为整数)分成六段
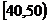 ,
,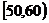 …
…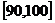 后得到如下部分频率分布直方图.
后得到如下部分频率分布直方图. 观察图形的信息,回答下列问题:
观察图形的信息,回答下列问题:
(1)求分数在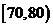 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次 考试的平均分;
考试的平均分;
(3)用分层抽样的方法在分数段为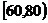 的学生中抽取一个容量为
的学生中抽取一个容量为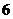 的样本,将该样本看成一个总体,从中任取
的样本,将该样本看成一个总体,从中任取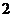 人,求至多有
人,求至多有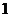 人在分数段
人在分数段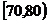 的概率.
的概率.
18.(本小题满分14分)
已知命题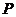 :函数
:函数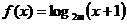 是增函数;命题
是增函数;命题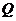 :
: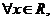
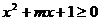 .
.
(1)写出命题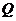 的否命题
的否命题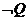 ;并求出实数
;并求出实数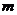 的取值范围,使得命题
的取值范围,使得命题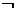
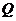 为真命题;
为真命题;
(2)如果“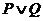 ” 为真命题,“
” 为真命题,“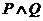 ”为假命题,求实数
”为假命题,求实数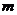 的取值范围.
的取值范围.
17.(本小题满分12分)
已知四棱锥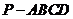 的三视图如下图所示,其中主视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.
的三视图如下图所示,其中主视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.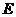 是侧棱
是侧棱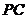 上的动点.
上的动点.
(1)求证: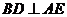
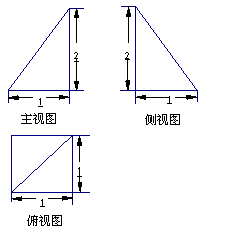
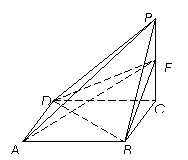 (2)若五点
(2)若五点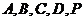 在同一球面上,求该球的体积.
在同一球面上,求该球的体积.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com