
19.(本小题满分12分)设数列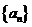 的前
的前 项和为
项和为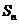 ,
,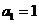 且对于任意正整数
且对于任意正整数 ,点
,点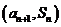 在直线
在直线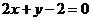 上.
上.
(1)求数列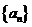 的通项公式;
的通项公式;
(2)设数列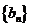 满足:
满足: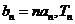 为数列
为数列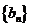 的前
的前 项和,求证:当
项和,求证:当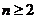 时,
时,
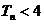 .
.
18.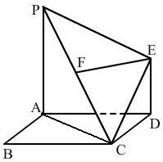 (本小题满分12分)如图,正方形
(本小题满分12分)如图,正方形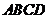 的边长为
的边长为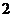 ,
,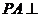 平面
平面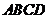 ,
,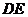 ∥
∥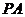 ,且
,且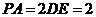 ,
,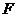 是
是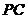 的中点.
的中点.
(1)求证: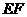 ∥平面
∥平面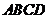 ;
;
(2)求证:平面PEC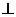 平面PAC;
平面PAC;
(3)求三棱锥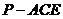 的体积
的体积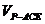 .
.
17.(本小题满分12分)已知向量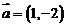 ,
,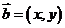 .
.
(1)若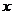 ,
,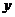 分别表示将一枚质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次时第一次、第二次出现的点数,求满足
分别表示将一枚质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次时第一次、第二次出现的点数,求满足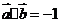 的概率;
的概率;
(2)若实数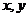
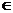
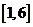 ,求满足
,求满足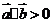 的概率.
的概率.
演算步骤(本答题共6小题,共75分)
16.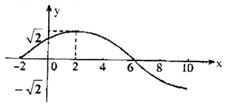 (本小题满分12分)已知函数
(本小题满分12分)已知函数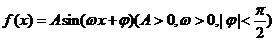 的部分图象如下图所示.
的部分图象如下图所示.
(1)求函数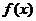 的解析式;
的解析式;
(2)若图象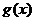 与函数
与函数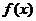 的图象关于
的图象关于
点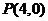 对称,求函数
对称,求函数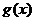 的单调递增区间.
的单调递增区间.
15.选做题(请考生在以下三个小题中任选一题做答,如果多做,则按所做的第一题评阅记分)
(1).(选修4-4坐标系与参数方程).已知曲线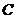 的参数方程为
的参数方程为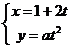
(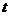 为参数,
为参数,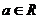 ),点
),点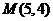 在曲线
在曲线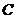 上,则曲线
上,则曲线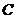 的普通方程为
.
的普通方程为
.
(2).(选修4-5不等式选讲)已知不等式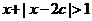 的解集为R,则正实数c的取值范围是
.
的解集为R,则正实数c的取值范围是
.
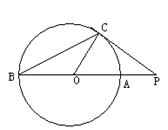
(3).(选修4-1几何证明选讲)如图,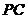 切
切
圆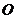 于点
于点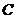 ,割线
,割线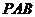 经过圆心
经过圆心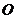 ,
,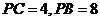 ,
,
则 .
.
14.等差数列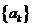 共有
共有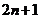 项
项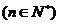 ,其
,其
中所有奇数项之和为310,所有偶数项之和为300,
则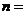 .
.
13.已知函数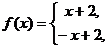
 则不等式
则不等式
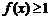 的解集为 .
的解集为 .
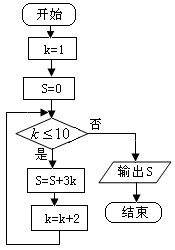
12.执行如右图所示的程序框图,则输出的
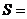 .
.
11. 抛物线
抛物线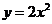 的准线方程是
.
的准线方程是
.
10.设实数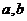 满足
满足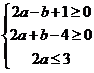 ,则
,则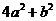
的最大值是
A.25 B.50 C.1 D.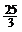
第Ⅱ卷 非选择题(共100分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com