20．(本小题满分12分)

已知椭圆：的离心率，点为椭圆的右焦点，点、分别为椭圆长轴的左、右顶点，点为椭圆的上顶点，且满足．

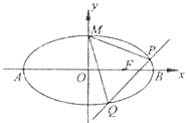(1)求椭圆的方程；

(2)是否存在直线，当直线交椭圆于，两点时，使点

恰为的垂心。若存在，求出直线的方程；若不存在，

请说明理由

19．(本小题满分12分)

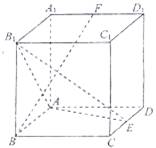　　 如图，在正方体中，、分别是、中点

(1)求证：；

(2)求证：平面；

(3)棱上是否存在点使，若存在，确定点

位置，若不存在，说明理由．

18．(本小题满分12分)

　　　 某班级举行一次知识竞赛活动，活动分为初赛和决赛两个阶段、现将初赛答卷成绩(得分均为整数，满分为100分)进行统计，制成如下频率分布表．

(1)填充频率分布表中的空格(在解答中直接写出对应空格序号的答案)；

(2)决赛规则如下：参加决赛的每位同学依次口答4道小题，答对2道题就终止答题，并获得一等奖。如果前三道题都答错，就不再答第四题。某同学进入决赛，每道题答对的概率的值恰好与频率分布表中不少于80分的频率的值相同．

①求该同学恰好答满4道题而获得一等奖的概率；

②记该同学决赛中答题个数为，求的分布列及数学期望．

17．(本小题满分12分)

已知等差数列满足．

(1)求数列的通项公式；

(2)设等比数列各项均为正数，其前项和，若，求．

16．向区域内任投一点，则点落在单位圆　　　　　　　　　 内的概率为　　　　　　　 ．

15．过原点作曲线的切线，则切线方程为　　　　　　 ．

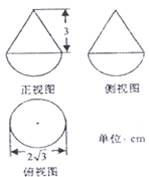
14．如图所示，某几何体的正视图、侧视图均为半圆和等边三角形的

　　 组合，俯视图为圆形，则该几何体的全面积为　　　　　 　．

13．函数的最小值为　　　　　　　 ．

12．已知定义域为的函数，则下列命题：

　　　 ①若恒成立，则函数的图像关于直线的对称；

　　　 ②若恒成立，则函数的图像关于(1，0)点对称；

　　　 ③函数的图像与函数的图像关于轴对称；

　　　 ④函数的图像与函数的图像关于原点对称；

　　　 ⑤若恒成立，则函数以4为周期．

　　　 其中真命题的有

　　　 A．①④　　　　　　　 B．②③　　　　　　　　 C．②⑤　　　　　　　 D．③⑤

第II卷(非选择题，共90分)

本卷包括必考题和选考题两部分，第13题-21题为必考题，每个试题考生都必须作答，第22题-24题为选考题，考生根据要求作答。

11．已知双曲线的两个焦点分别为，，为双曲线上的一点，且°,则

　　　 A．　　　　　　　　 B．1　　　　　　　　　　 C．2　　　　　　　　　　 D．4