3．各类晶体主要特征

在离子晶体、原子晶体和金属晶体中均不存在分子，因此NaCl、SiO₂等均为化学式。只有分子晶体中才存在分子。

2．对一些重要的知识点加以总结归纳

如，在元素周期律的学习中用多种方法判断元素的金属性和元素的非金属性，并加以归纳总结。

金属性强弱：(1)单质与水或非氧化性酸反应难易；(2)单质的还原性(或离子的氧化性)；(3)M(OH)_n的碱性；(4)置换反应；(5)原电池中正负极判断，金属腐蚀难易；(4)对应金属离子电解时阴极放电顺序。

非金属性强弱：(1)与氢气反应生成气态氢化物难易；(2)单质的氧化性(或离子的还原性)；(3)最高价氧化物的水化物(H_nRO_m)的酸性强弱；(4)置换反应。

1．原子结构和元素周期律知识的综合网络

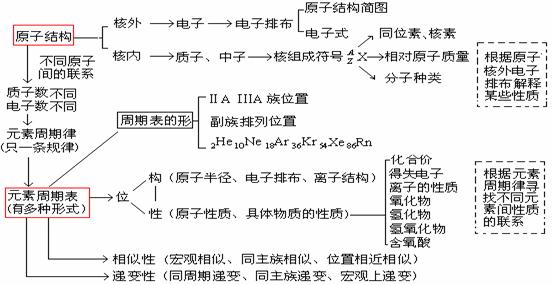
3．要注意，这部分内容也属于最重要基础知识之一，可以联系到各部分内容中，编制成多种不同的题型进行考查。

[复习重点]

2．《考试大纲》中有关物质结构部分的内容还有：

(1)理解离子键、共价键的涵义。理解极性键和非极性键。了解极性分子和非极性分子。了解分子间作用力，初步了解氢键。能用有关原理解释一些实际问题。

(2)了解几种晶体类型(离子晶体、原子晶体、分子晶体和金属晶体)及其性质，了解各类晶体内部微粒间的相互作用。能够根据晶体的性质判断晶体类型等。

(3)能对原子、分子、化学键等微观结构进行三维空间想像，重视理论联系实际、用物质结构理论解释一些具体问题。

高考试题中常常是结合元素化合物内容进行综合考查。题型上看可以是选的择题、简答题、填空题等。

1．《考试大纲》对物质结构、元素周期律方面的要求为：以第3周期为例，掌握同一周期内元素性质(如：原子半径、化合价、单质及化合物性质)的递变规律与原子结构的关系；以ⅠA和ⅦA族为例，掌握同一主族内元素性质递变规律与原子结构的关系。这部分内容每年都会有试题，可以是选择题，也可以有关结合物质结构的元素化合物推断题。

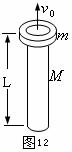
例题8.如图12所示，长为、质量为的圆柱形木棒竖直放置，在其顶部套有一质量为的薄铁环，当棒和环有相对运动时，棒和环之间有大小恒为(＞)的摩擦力。现突然在棒的下端给棒一个很大的冲击力，使棒瞬间具有竖直向上的初速度，试求：

⑴若要使铁环在木棒落地之前不滑离木棒，此木棒的长度不能少于多少？

⑵设木棒足够长，求棒上升的最大高度？

解析：⑴经过分析可知，为使铁环在木棒落地之前不滑离木棒，只需铁环与木棒具有向上的共同速度时不滑离木棒即可。

设铁环的加速度大小为，由于＞1，故方向向上；木棒的加速度大小为，方向向下。则有

对于铁环　　

对于木棒　　

木棒相对于铁环的加速度为

解以上几式得

再由匀变速直线运动规律公式得

解得　　　　

木棒的长度为

　　　　　　 ≥

所以木棒的最小长度为

⑵铁环和木棒的速度相等时，对于铁环和木棒分别有

解得　　　　

设此时木棒上升的高度为，以木棒的初速度方向为正方向，则

解得　　　　

命题解读：本题涉及到物体的受力分析、牛顿第二定律、运动学规律和相对运动等规律，是典型的综合问题，重在考查灵活运用牛顿定律和运动学规律求解关联问题的能力，这也是高考综合分析计算题命题的重点和热点。

例题7.用质量为、长度为的绳子沿光滑水平面拉动质量为的物体，在绳子的一端施加的水平拉力为，如图10所示，试求：

⑴物体与绳子的加速度；

⑵绳子中各处张力的大小(假定绳子的质量分布均匀，下垂可以忽略)。

解析：⑴以物体和绳子为研究对象，根据牛顿第二定律得

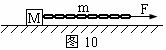
所以　

方向与力的方向是相同的，即水平向右。

⑵再以物体和靠近物体的长度为的一部分绳子为研究对象如图11所示。根据牛顿第二定律，得

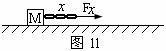
由上式可知，绳子中各处张力的大小是不同的，离物体越近的地方张力越小，当时，绳子施加于物体上的力为。

命题解读：一般情况下我们研究的都是轻绳，其质量是可以忽略不计的，只考虑它由于发生弹性形变而产生的弹力，从这道题可以看出，绳子的质量不能忽略时，是可以把它和其它的物体一样对待的；整体分析法也不是万能的，隔离法乃是解决牛顿运动定律问题的基本方法，在分析整体内部各部分之间的相互作用时必须应用隔离法，在解决具体问题时要具体分析，两种方法要灵活运用。

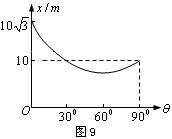例题6.一物体在斜面上以一定的初速度向上运动，斜面的倾角可在-之间变化，设物体所能达到的最大位移与斜面倾角之间的关系如图9所示，试求当多大时有最小值？这个最小值是多大？

解析：设物体的初速度为，在斜面上滑行时的加速度大小为，则

当时，物体做竖直上抛运动，由图可知上升的最大高度为，则

所以　

当时，物体沿水平面作匀减速直线运动，由图可知此时滑行的最大距离为，则

故　　

将和的值代入上面的表达式，在利用数学知识整理可得当时，位移有最小值，将代入得

所以物体最大位移的最小值为

命题解读：应用数学知识解决物理问题是高考考察的能力之一，除本题应用的三角函数变换以外，还有如数学归纳法、二次函数极值等都是解决物理问题的强有力工具，不论是在力学还是电学，好多的物理应用题中都有所涉及，高考计算题中也多次出现，平常学习时请注意掌握。

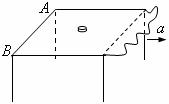例题5.如图8所示，一小圆盘静止在桌布上，位于方桌水平面的中央，桌布的一边与方桌的边重合，已知盘与桌布间的动摩擦因数为，盘与桌面间的动摩擦因数为，现突然以恒定加速度将桌布抽离桌面，加速度方向是水平的且垂直于，若圆盘最后没从桌面上掉下，则加速度应满足的条件是什么？(以表示重力加速度)

桌布抽出后，圆盘在桌面上时，又有

设圆盘刚离开桌布时的速度为，移动的位移为，离开桌布后在桌面上再运动后便停下，由匀变速直线运动规律公式，得

　　　 ≤

设桌布从圆盘下抽出所经历的时间为在这段时间内桌布发生的位移为，则

解以上各式，得

　　　 ≥_[来源:]

命题解读：本题是一道牛顿第二定律的应用题，解题的其中一个关键就是要分析出圆盘在两个运动阶段的加速度不同；另一个关键则是要分析出圆盘布从桌面掉下的临界条件是≤，这才是解题的难点。