19、解：(Ⅰ) 连结,取中点，连结,

因为平面,所以平面平面，

又底面为菱形，为中点，

所以平面，

因为∥，

所以平面，

又==，

所以点到平面的距离为.　

(Ⅱ)方法一：

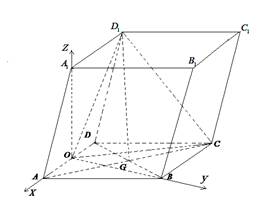分别以所在直线为轴，建立如图所示的坐标系，

则 ，，所以，

面的一个法向量，

所以，解得，

因为面的一个法向量为，

设面的一个法向量为，则，，

则有所以，

取，，　

则，

所以二面角的大小为.　

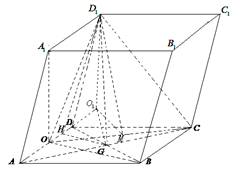
方法二:连结,由(1)可知为直线 与平面所成角.

则，

所以

过做垂直,交其延长线于点，连结,在中，，所以，

那么在直角三角形，=1，

过做于点，连结，

则为所求二面角的平面角，　

连结,则，且=2，，

则在△中，，

所以，

所以所求二面角的大小为。

18、解：记“该地美术馆选送的中国画、书法、油画中恰有i件作品入选‘中国馆·贵宾厅’”为事件Ai(i＝0，1，2，3)，记“代表作中萄艺入选‘中国馆·贵宾厅’”为事件B。

(1)该地美术馆选送的四件代表作中有一件作品中恰有一件作品入选“中国馆·贵宾厅”的概率为：

(II)取值为0，1，2，3，4，该地美术馆选送的四件代表作品中没有作品入选“中国馆·贵宾厅”的概率为

该地美术馆选送的四件代表作品中恰有两件作品入选“中国馆·贵宾厅”的概率为

该地美术馆选送的四件代表作中恰有三件作品入选“中国馆·贵宾厅”的概率为：

该地美术馆选送的四件代表作品全部入选“中国馆·贵宾厅”的概率为

∴随机变量的分布列为

	0	1	2	3	4
p

∴随机变量的数学期望

17、解：(1)

由题意知，周期，

(I)∵的周期T＝4，

13、128　　　　 14、1；　 1　　　　　 15、　　 16、①②④

22、设数列{a_n}满足：

(1)求a₂，a₃；(2)令，求数列{b_n}的通项公式；

(3)已知，求证：。 参考答案

1-5　 CCBDD　　 6-10　 CCAAC　　 11-12　 CB

21、(1)已知动点P(x，y)到点F(0，1)与到直线y＝－1的距离相等，求点P的轨迹L的方程；

(2)若正方形的三个顶点，，()在(1)中的曲线上，设的斜率为，，求关于的函数解析式；

(3)求(2)中正方形面积的最小值。

20、已知函数(，实数，为常数)．

(1)若()，且函数在上的最小值为0，求的值；

(2)若对于任意的实数，，函数在区间上总是减函数，对每个给定的n，求的最大值h(n)．

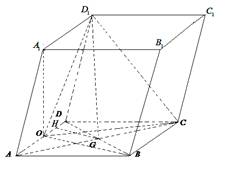
19、如图，平行六面体ABCD-中，底面ABCD是边长为2的菱形，∠BAD=，

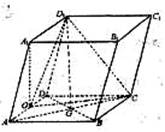　 　其中AC与BD交于点G，点在面ABCD上的射影0恰好为线段AD的中点。

(I)求点G到平面距离；

(Ⅱ)若与平面所成角的正弦值为，

　　　　 求二面角-OC-D的大小．

18、“上海世博会”将于2010年5月1日至10月31日在上海举行。世博会“中国馆·贵宾厅”作为接待中外贵宾的重要场所，陈列其中的艺术品是体现兼容并蓄、海纳百川的重要文化载体，为此，上海世博会事物协调局将举办“中国2010年上海世博会‘中国馆·贵宾厅’艺术品方案征集”活动。某地美术馆从馆藏的中国画、书法、油画、陶艺作品中各选一件代表作参与应征，假设代表作中中国画、书法、油画入选“中国馆·贵宾厅”的概率均为，陶艺入选“中国馆·的概率为”，(I)求该地美术馆选送的四件代表作中恰有一件作品入选“中国馆·贵宾厅”的概率。(II)设该地美书馆选送的四件代表作中入选“中国馆·贵宾厅”的作品件数为随机变量，求的数学期望。

17、已知向量，函数＝

的图象过点M，且相邻两对称轴之间的距离为2，

(1)求的表达式；(2)求的值