1.若AB线位于同一经线圈，2010年元旦时，A为太阳直射点，则　

　 A.A、B的纬度值互余　　　　　 B.A、B纬度值相等

　 C.B正值极夜现象　　　 　　　　 D.A、B在同一经线上

19．[文科]　 解：由体积为，得，所以h=4… 3分

取AD的中点为E，联结PE，PB，则，　 　　　……5分

，为直线PB与直线所成的角． 　　　　……8分

经计算，，　 　　　　　　　　　　　　…… 10分

，

即异面直线与所成的角为(或)．… 12分

[理科]　 解：取AD的中点为E，联结BE，PB，则，

为PB与平面所成的角．　　　 　　　　　　　…… 2分

经计算，，， …… 4分

以为x轴，OB为y轴，为z轴建立空间直角坐标系，… 5分

，，，

，，　 　　　　　　…… 7分

设平面的法向量，

由得，　　　 　　　　　　　　　… 10分

而，所以 …… 12分

19. (2010年4月上海杨浦、静安、青浦、宝山四区联合高考模拟) (本题满分12分)

[文科]已知是底面为菱形的直四棱柱，P是棱的中点，，底面边长为2，四棱柱的体积为，求异面直线与所成的角大小.(结果用反三角函数值表示)

是棱的中点，，底面边长为2，

若与平面成角，求点到平面的距离.

19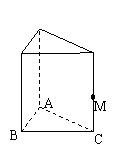．(上海市浦东新区2010年4月高考预测理科)(本题满分14分)本题共有2个小题，第1小题满分6分，第2小题满分8分.

直三棱柱中，底面为等腰直角三角形, 且，

，, 是侧棱上一点, 设.

(1)若，求的值；　　　　　　　　　　　　　　　　

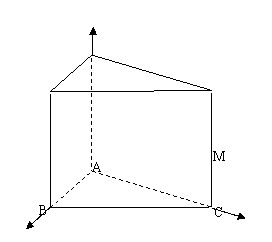(2)若直线与平面所成的角为，求多面体的体积.

解：(1)以为坐标原点，以射线、、分别为、、轴建立空间直角坐标系，如图所示，则,，,…………………………………………2分

，…………………………2分

由得，，即

解得………………………………………………………2分

(2)由题意知，平面的一个法向量为，　　

……………………………………………………………………………………2分

因为直线与平面所成的角为，所以解得…………………2分

三棱锥的体积

三棱柱体积…………………………………………………2分

所以多面体的体积……………………………………2分

17．(1)由平行六面体的性质，知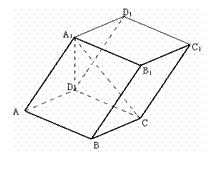

直线与该平行六面体各侧面所成角的大小有两个，

其一是直线与侧面所成角的大小，记为；

其二是直线与侧面所成角的大小，记为．

，，即

又平面，

平面，

所以，即为所求．……………………………2分

所以，………………………………1分

分别以，，为，，轴建立空间直角坐标系，

可求得，侧面的法向量，

所以，与所在直线的夹角为

或．

所以，直线与侧面所成角的大小为或．…3分

综上，直线与该平行六面体各侧面所成角的最大值为． …………1分

(2)由已知，有，　　　 …………………………………………………1分

由面积公式，可求四边形的面积为，…………………………………2分

平行六面体的体积．……………2分

所以，平行六面体的体积的取值范围为． ……………2分

17．(上海市闸北区2010年4月高三第二次模拟理科)(满分14分)本题有2小题，第1小题7分，第2小题7分．

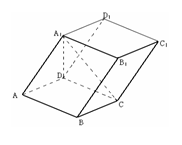如图，在平行六面体中，，，平面， 与底面所成角为，．

(1)若，求直线与该平行六面体各侧面所成角的最大值；

(2)求平行六面体的体积的取值范围．

20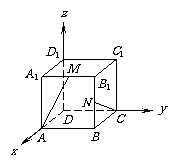． 解： 如图建立空间直角坐标系,则A(1，0，0)，C(0，1，0)，，

=₍0，，1₎，=₍1，0，₎ (其中)-----4分

　设向量、 的夹角为，

则，

-------------------------------------------------10分

或，无解；-----------------------------------12分

所以当时，， -------------------------------------------------------------------------14分

20．(上海市徐汇区2010年4月高三第二次模拟理科)(本题满分14分)

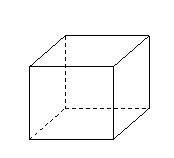(如图)已知正方体的棱长均为1，为棱上的点，为棱的中点，异面直线与所成角的大小为，求的值.

20．(上海市松江区2010年4月高考模拟理科)(本题14分，其中第(1)小题6分，第(2)小题8分)

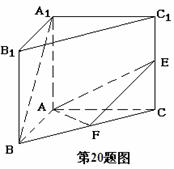设在直三棱柱中，，，依次为的中点．

(1)求异面直线、所成角的大小(用反三角函数值表示)；

(2)求点到平面的距离．

解：以A为原点建立如图空间坐标系，则各点坐标为，，

，，…………2分

(1)，，

∴…………6分

(2)设平面的一个法向量为，∵，

由　 得　 令 可得　 …………10分

∵　 ∴…………13分

∴点到平面的距离为．…………14分

19、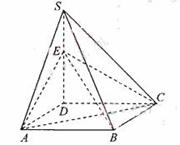解：(1)以为坐标原点，建立空间直角坐标系。

　。设

则 …………………………………………2分　　　　　　　　　　　　　　　　　　　　　　　　　　

，

…………………………………………………4分

。

…………………………………………………………6分

(2)取平面的一个法向量为。………………………………7分

设平面的一个法向量为，，由得，

。取，………………………………………………10分

由……………………………………………12分

得，因此。……………………………………………14分

(如用其它解法，请对照给分)