19、(上海市长宁区2010年高三第二次模拟理科)(本题满分14分，第(1)小题6分，第(2)小题8分)

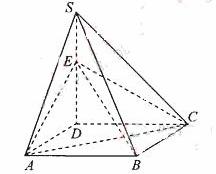　如图，四棱锥S-ABCD的底面是正方形，

SD⊥平面ABCD,SD＝AD＝,点E是线段SD上任意一点。　

(1)求证：AC⊥BE；

(2)若二面角C-AE-D的大小为，求线段的长。

19、(本题满分14分)本题共有2个小题，第1小题满分7分，第2小题满分7分．

证明　 (1)(反证法)假设直线与不是异面直线. ……………………………1分

设直线与都在平面上，则.………………………3分

因此，有不共线的三个公共点，即

重合).又长方体的相邻两个面不重合，这是矛盾，于是，假设不成立. …………………………………………………………6分

　所以直线与是异面直线. 　　　　　　 …………………7分

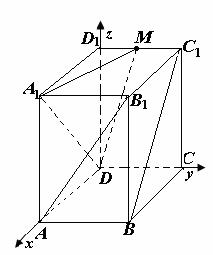
解　 (2)按如图所示建立空间直角坐标系，可得有关点的坐标为D(0，0，0)、

A(4，0，0)、B(4，2，0)，C(0，2，0)，(4，0，4)，(4，2，4)，(0，2，4)，

(0，0，4)．于是，M(0，1，4)，．……9分

　设平面的法向量为，则

，即．取．　 　…　 11分

　所以平面的一个法向量为．

记直线为，于是，

，．　 ………………………13分

　所以，直线为＝．…………………14分

19．(上海市嘉定黄浦2010年4月高考模拟理科)(本题满分14分)本题共有2个小题，第1小题满分7分，第2小题满分7分．

已知长方体，，点M是棱的中点．

(1)试用反证法证明直线是异面直线；

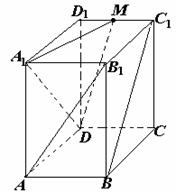(2)求直线所成的角(结果用反三角函数值表示)．

19．解：由三棱柱是直三棱柱，

　 ==24　　 (4分)

=　 (4分)

　此容器最多能盛水　 　　(4分)

19、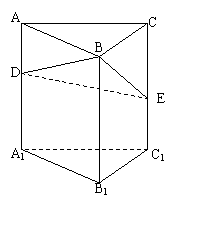(上海市奉贤区2010年4月高三质量调研文科)(本题满分12分)如图，已知三棱柱是直三棱柱，，若, ,,D、E分别在棱和上，且，，若用此直三棱柱作为无盖盛水容器，且在D、E两处发生泄露，试问现在此容器最多能盛水多少()？

19．解：由三棱柱是直三棱柱，

==10,　 得:　 (4分)

_[来源:]

==2.5　 (4分)

　此容器最多能盛水：　 　=7.5 (L)　 (4分)

19、(上海市奉贤区2010年4月高三质量调研理科)(本题满分12分)

如图，已知三棱柱是直三棱柱，，若用此直三棱柱作为无盖盛水容器，容积为,高为，盛水时发现在D、E两处有泄露，且D、E分别在棱和上， ， 。试问现在此容器最多能盛水多少()？

20．(本题满分14分)本题共有2个小题，第1小题满分6分，第2小题满分8分．

解：(1)设，由题设，

得，即，解得．

故的长为．(6分)

(2)因为在长方体中//，所以即为异面直线与所成的角(或其补角)．(8分)

在△中，计算可得，则的余弦值为，

故异面直线与所成角的大小为．(14分)

20．(上海市卢湾区2010年4月高考模拟考试文科)(本题满分14分)本题共有2个小题，第1小题满分6分，第2小题满分8分．

在长方体中，，过、、三点的平面截去长方体的一个角后，得到如图所示的几何体，且这个几何体的体积为．

(1)求棱的长；

(2)若的中点为，求异面直线与所成角的大小(结果用反三角函数值表示)．

20．(本题满分14分)本题共有2个小题，第1小题满分6分，第2小题满分8分．

解：(1)设，由题设，

得，即，解得．

故的长为．(6分)

(2)以点为坐标原点，分别以，，所在的直线为轴，轴，轴建立空间直角坐标系．

由已知及(1)，可知，，，，

设平面的法向量为，有，，

其中，，则有即解得，，取，得平面的一个法向量，且．(12分)

在平面上取点，可得向量，于是点到平面的距离．(14分)