
3.若 ,则
,则 角的终边在
( ▲ )
角的终边在
( ▲ )
A.第一、二象限 B.第二、三象限 C.第一、四象限 D.第三、四象限
4在等差数列 中第一个负数是
( ▲ )
中第一个负数是
( ▲ )
A.第13项 B.第14项 C.第15项 D.第16项
2.已知数列 满足:
满足: ,且
,且 ,则
,则 的值为 ( ▲ )
的值为 ( ▲ )
A. B.
B. C.
C. D.
D.
1. 的值是
( ▲ )
的值是
( ▲ )
A. B.
B. C.
C. D.
D.
21.(本小题满分14分)
解:(Ⅰ) ,则
,则 ,
, ,又
,又 ,
,
 …………2分
…………2分
(Ⅱ)令
 ,则
,则
 ,…3分
,…3分
令 ,得
,得 ,且
,且 ,
,
当 为正偶数时,随
为正偶数时,随 的变化,
的变化, 与
与 的变化如下:
的变化如下:
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
0 |
 |
0 |
 |
 |
 |
 |
 |
|
 |
极大值 |
 |
极小值 |
 |
所以当 时,
时, 极大=
极大= ;当
;当 时,
时, 极小=0.…………7分
极小=0.…………7分
当 为正奇数时,随
为正奇数时,随 的变化,
的变化, 与
与 的变化如下:
的变化如下:
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
0 |
 |
0 |
 |
 |
 |
 |
 |
|
 |
极大值 |
 |
|
 |
所以当 时,
时, 极大=
极大= ;无极小值.…………10分
;无极小值.…………10分
(Ⅲ)由(Ⅰ)知, ,即
,即 ,
,
所以方程为 ,…………11分
,…………11分
 ,…………12分
,…………12分
又 ,而对于
,而对于 ,有
,有 (利用二项式定理可证),
(利用二项式定理可证),
 。…………13分
。…………13分
综上,对于任意给定的正整数 ,方程只有唯一实根,且总在区间
,方程只有唯一实根,且总在区间 内,所以原方程在区间
内,所以原方程在区间 上有唯一实根.…………14分
上有唯一实根.…………14分
20.(本小题满分14分)
解:(Ⅰ)由 得,
得, 。由题设知
。由题设知 为该方程的两个根。
为该方程的两个根。

(Ⅱ)若c=2,则b=2.
 …①,又由
…①,又由 ………②
………②
②式-①式可得:


当 =1时,有
=1时,有


……………6分
故
(Ⅲ)
以下首先证明不等式
事实上要证
则
 另一方面我们又设函数
另一方面我们又设函数 ,则
,则
 。
。
故 在
在 上单调递减,
上单调递减,
我们取
综上:
分别令 =1,2,3,…,2009得:
=1,2,3,…,2009得:

将这2009个式子累加得:
19.(本小题满分13分)
解法一: (Ⅰ)设椭圆方程为
 ,由已知
,由已知 。
。
又 .
.
所以 ,椭圆C的方程是
,椭圆C的方程是 +
+  =1.…………4分
=1.…………4分
(Ⅱ)若直线l与x轴重合,则以AB为直径的圆是x2+y2=1, …………5分
若直线l垂直于x轴,则以AB为直径的圆是(x+ )2+y2=
)2+y2= .…………6分
.…………6分
由 解得
解得 即两圆相切于点(1,0).…………7分
即两圆相切于点(1,0).…………7分
因此所求的点T如果存在,只能是(1,0).
事实上,点T(1,0)就是所求的点.证明如下:
当直线l垂直于x轴时,以AB为直径的圆过点T(1,0).
若直线l不垂直于x轴,可设直线l:y=k(x+ ).
).
由 即(k2+2)x2+
即(k2+2)x2+ k2x+
k2x+ k2-2=0.………………9分
k2-2=0.………………9分
记点A(x1,y1),B(x2,y2),则 ………………10分
………………10分
又因为 =(x1-1, y1),
=(x1-1, y1),  =(x2-1, y2),
=(x2-1, y2),
 ·
· =(x1-1)(x2-1)+y1y2=(x1-1)(x2-1)+k2(x1+
=(x1-1)(x2-1)+y1y2=(x1-1)(x2-1)+k2(x1+ )(x2+
)(x2+ )
)
=(k2+1)x1x2+( k2-1)(x1+x2)+
k2-1)(x1+x2)+ k2+1
k2+1
=(k2+1)
 +(
+( k2-1)
k2-1)  +
+  +1=0,
+1=0,
所以TA⊥TB,即以AB为直径的圆恒过点T(1,0).
所以在坐标平面上存在一个定点T(1,0)满足条件.…………13分
解法二:(Ⅰ)由已知 ,设椭圆C的方程是
,设椭圆C的方程是
 .
.
因为点P在椭圆C上,所以 ,解得
,解得 ,
,
所以椭圆C的方程是: .………………4分
.………………4分
(Ⅱ)假设存在定点T(u,v)满足条件.
同解法一得(k2+2)x2+ k2x+
k2x+ k2-2=0.………………6分
k2-2=0.………………6分
记点A(x1,y1),B(x2,y2),则 …………7分
…………7分
又因为 =(x1-u, y1-v),
=(x1-u, y1-v),  =(x2-u, y2-v),及y1=k(x1+
=(x2-u, y2-v),及y1=k(x1+ ),y2=k(x2+
),y2=k(x2+ ).
).
所以 ·
· =(x1-u)(x2-u)+(y1-v)(y2-v)
=(x1-u)(x2-u)+(y1-v)(y2-v)
=(k2+1)x1x2+( k2-u-kv)(x1+x2)+
k2-u-kv)(x1+x2)+ k2-
k2- v+u2+v2
v+u2+v2
=(k2+1)
 +(
+( k2-u-kv)·
k2-u-kv)· +
+  -
- v + u2+v2,
v + u2+v2,
= .…………10分
.…………10分
当且仅当 ·
· =0恒成立时,以AB为直径的圆恒过点T.
=0恒成立时,以AB为直径的圆恒过点T.
 ·
· =0恒成立等价于
=0恒成立等价于 解得u=1,v=0.此时,以AB为直径的圆恒过定点T(1,0).……………………13分
解得u=1,v=0.此时,以AB为直径的圆恒过定点T(1,0).……………………13分
当直线l垂直于x轴时,以AB为直径的圆 亦过点T(1,0).
亦过点T(1,0).
所以在坐标平面上存在一个定点T(1,O)满足条件.…………13分
解法三:(Ⅰ)同解法一或解法二.………………4分
(Ⅱ)设坐标平面上存在一个定点T满足条件,根据直线过x轴上的定点S及椭圆的对称性,所求的点T如果存在,只能在x轴上,设T(t,O).……5分
同解法一得 ………………7分
………………7分
又因为 =(x1-t, y1),
=(x1-t, y1),
 =(x2-t, y2),所以
=(x2-t, y2),所以
 ·
· =(x1-t)(x2-t)+y1y2=(x1-t)(x2-t)+k2(x1+
=(x1-t)(x2-t)+y1y2=(x1-t)(x2-t)+k2(x1+ )(x2+
)(x2+ )
)
=(k2+1)x1x2+( k2-t)(x1+x2)+
k2-t)(x1+x2)+ k2+t 2
k2+t 2
=(k2+1)
 +(
+( k2-t)
k2-t) +
+ +t2
+t2
=  .…………………………10分
.…………………………10分
当且仅当 ·
· =O恒成立时,以AB为直径的圆恒过点T.
=O恒成立时,以AB为直径的圆恒过点T.
 ·
· =O恒成立等价于
=O恒成立等价于 解得t=1.
解得t=1.
所以当t=1时,以AB为直径的圆恒过点T.……………………12分
当直线l垂直于x轴时,以AB为直径的圆 亦过点T(1,O).
亦过点T(1,O).
所以在坐标平面上存在一个定点T(1,O)满足条件.………………13分
18.(本小题满分12分)
解法1:(Ⅰ)过
 ,且
,且 ,则
,则 为异面直线
为异面直线 与
与 所成的角.
所成的角. .……3分
.……3分
(Ⅱ) 为
为 的中点。
的中点。
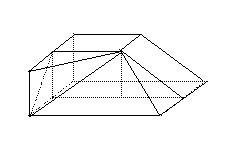 ∵
∵ 为
为 的中点,∴
的中点,∴ 平面
平面 ,从而
,从而 。……5分
。……5分
∵ ,……6分
,……6分
∴ 平面
平面 .………7分
.………7分
(Ⅲ)由 平面
平面 ,得
,得
 .
.
又由(2) 平面
平面 ,∴由三垂线定理得,
,∴由三垂线定理得,
 ,∴
,∴ 是二面角
是二面角 的平面角.…………10分
的平面角.…………10分
∵ ,∴
,∴ .即二面角
.即二面角 的余弦值为
的余弦值为 .…………12分
.…………12分
解法2:以 为坐标原点,
为坐标原点, 所在直线分别为
所在直线分别为 轴建立直角坐标系.…2分
轴建立直角坐标系.…2分
(Ⅰ)∵ ,
, ,∴
,∴ .……3分
.……3分
(Ⅱ)设 ,∵
,∵ ,
, ,
, .……
.……
……6分
由 平面
平面 得,
得, ∴
∴ ∴
∴ ,即
,即 为
为 的中点.
的中点.
…………7分
(Ⅲ)由(2)知, 为平面
为平面 的一个法向量.
的一个法向量.
设 为平面
为平面 的一个法向量,则
的一个法向量,则 ,
, .
.
由
 令
令 .∴
.∴ .……10分
.……10分
∴ ,即二面角
,即二面角 的余弦值为
的余弦值为 .…………12分
.…………12分
17.(本小题满分12分)
解:记选手甲第一、二、三次射击命中目标分别为事件 、
、 、
、 ,三次均为击中目标为事件
,三次均为击中目标为事件 ,则
,则 .
.
设选手甲在 m处击中目标的概率为
m处击中目标的概率为 ,则
,则 .由
.由 m时
m时 ,得
,得 ,∴
,∴ ,
, .∴
.∴
 .…………4分
.…………4分
(Ⅰ)由于各次射击都是相互独立的,所以选手甲在三次射击中击中目标的概率为
 .…………7分
.…………7分
(Ⅱ)由题设知, 的可取值为
的可取值为 .
.
 ,
, ,
, ,
, .
.
∴ 的分布列为
的分布列为
 |
0 |
1 |
2 |
3 |
 |
 |
 |
 |
 |
数学期望为 .…………12分
.…………12分
16.(本小题满分10分)
解:(Ⅰ)取AB、AC的中点E、F,则
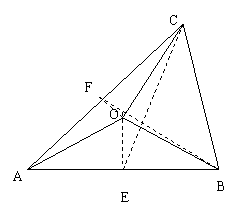
 ………3分
………3分
同理 ;
;
所以 。………5分
。………5分
(Ⅱ)
 ……10分
……10分
11. ;12.
;12. ;13.
;13. ;14.
;14. ;15.
;15. 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com