19. (本题12分) 已知函数的定义域为R.

(1) 当时, 求的单调递增区间;

(2) 设, 若为偶函数, 求的值.

18. (本题12分) 美国蓝球职业联赛(NBA)某赛季的总决赛在湖人队与活塞队之间进行, 比赛采取

七局四胜制, 即若有一队胜四场,则此队获胜且比赛结束. 因两队实力非常接近,在每场比赛

中每队获胜是等可能的.据资料统计, 每场比赛组织者可获门票收入100美元. 问:

(1) 组织者在此次决赛中获门票收入恰为400万美元的概率为多少?

(2) 组织者在此次决赛中获门票收入不少于600万美元的概率为多少?

17.(本题12分)已知函数满足且对于任意, 恒有

成立.

(1) 求实数的值;

(2) 解不等式.

16. 下图是某企业2000年至2003年四年来关于生产销售的一张统计图表 (注: 利润＝销售额－

生产成本). 对这四年有以下几种说法:

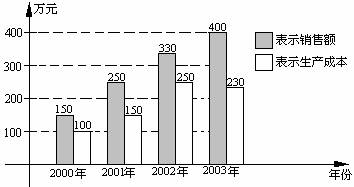(1) 该企业的利润逐年提高;

(2) 2000年-2001年该企业销

售额增长率最快;

(3) 2001年-2002年该企业生

产成本增长率最快;

(4) 2002年-2003年该企业利

润增长幅度比2000年-2001年

利润增长幅度大.

其中说法正确的是　　　　　

(注:把你认为正确的说法序号都

填上).

15. 如果函数在区间上是减函数,那么实数m的取值

范围是　 　　　　　　　　　　　.

14. 已知双曲线中心在坐标原点, 一个焦点坐标为, 一条渐近线方程为, 则双

曲线的标准方程为　　　　　　　　　　 .

13. 已知的展开式中的常数项是第七项, 则正整数n的值为　　　　　　　 .

12.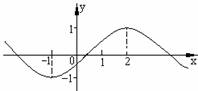 已知函数的图象如图所示, 则函数

的单调递减区间是　　　 (　 )

A. 　　　　B. 　　　　　　　

C. 　　　　D.

11. 已知函数的反函数为,若,则的最小值为(　 　)

A. 　　　　　　　　　B. 　　　　　　　　　　C. 　　 　　　　　　　　 D. 1

10. 已知函数是奇函数, 则函数的图象关于　　　　　　　　　 (　 )

A.　 直线对称　 　　　　　　　　　　　　　　　　　　　B.　 直线对称　　　 　

　 C. 　点对称　　　　 　　　　　　　　　　　　　　　　　D. 　点对称