
2.若 满足不等式组
满足不等式组 且
且 的最小值为
的最小值为 ,则
,则
1.若函数 在区间
在区间 上的最大值是最小值的3倍,则
上的最大值是最小值的3倍,则
|
装置 |
原理图 |
规律 |
||
|
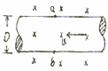
速度选择器 |
|
若 粒子做匀速直线运动 粒子做匀速直线运动 |
||
|
磁流体发电机 |
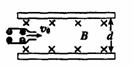
|









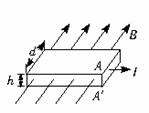
 的高频交流电源两极,带电粒子在窄缝间电场加速,在D形盒内偏转
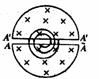
的高频交流电源两极,带电粒子在窄缝间电场加速,在D形盒内偏转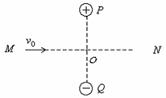 [例8]如图所示,PQ是空间位置固定的两个电荷量相等的异种电荷,它们的连线中点为O,MN是中垂线,两电荷连线与中垂线在纸平面内,在垂直纸面方向有一磁场,中垂线上一不计重力的带正电粒子以初速度v0保持沿中垂线运动,则
[例8]如图所示,PQ是空间位置固定的两个电荷量相等的异种电荷,它们的连线中点为O,MN是中垂线,两电荷连线与中垂线在纸平面内,在垂直纸面方向有一磁场,中垂线上一不计重力的带正电粒子以初速度v0保持沿中垂线运动,则
A.磁场的方向垂直纸面向外
B.带电粒子做匀速直线运动,所受洛仑兹力的大小不变
C.带电粒子做匀速直线运动,所受洛仑兹力的大小改变
D.带电粒子做变速直线运动,所受洛仑兹力的大小改变
[例8]C
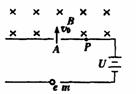
 [例9]如图所示,厚度为h,宽度为d的导体板放在垂直于它的磁感应强度为B的匀强磁场中,当电流通过导体板时,在导体板的上侧面A和下侧面A′之间会产生电势差,这种现象称为霍尔效应.实验表明,当磁场不太强时,电势差U、电流I和B的关系为U=k
[例9]如图所示,厚度为h,宽度为d的导体板放在垂直于它的磁感应强度为B的匀强磁场中,当电流通过导体板时,在导体板的上侧面A和下侧面A′之间会产生电势差,这种现象称为霍尔效应.实验表明,当磁场不太强时,电势差U、电流I和B的关系为U=k ,式中的比例系数k称为霍尔系数.霍尔效应可解释如下:外部磁场的洛伦兹力使运动的电子聚集在导体板一侧,在导体板的两侧将出现匀强电场,电子将受到静电力作用.当静电力与洛伦兹力平衡时,两侧之间就会形成稳定的电势差.设电流I是由电子的定向移动而形成的,电子的平均速率为v,电量为e.回答下列问题:
,式中的比例系数k称为霍尔系数.霍尔效应可解释如下:外部磁场的洛伦兹力使运动的电子聚集在导体板一侧,在导体板的两侧将出现匀强电场,电子将受到静电力作用.当静电力与洛伦兹力平衡时,两侧之间就会形成稳定的电势差.设电流I是由电子的定向移动而形成的,电子的平均速率为v,电量为e.回答下列问题:
(1)达到稳定状态时,导体板上侧面A的电势______下侧面A′的电势.(填“高于”、“低于”或“等于”)
(2)所受洛伦兹力的大小为______.
(3)当导体板上、下两侧面之间的电势差为U时,电子所受静电力的大小为______.
(4)由静电力和洛伦兹力平衡的条件,证明霍尔系数k=1/ne,n代表单位体积中自由电子的个数.
[例9](1)低于;(2)F洛=Bev;(3)F电=Bev;(4)k=Ud/IB=
3、带电粒子的轨道圆心(O)、速度偏向角()是指末速度与初速度之间的夹角、回旋角(a)一段圆弧所对应的圆心角叫回旋角、和弦切角(q)圆弧的弦与过弦的端点处的切线之间的夹角叫弦切角。
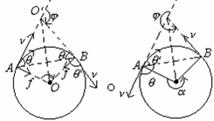 在分析和解答带电粒子作匀速圆周运动的问题时,除了应熟悉上述基本规律之外,还必须掌握确定轨道圆心的基本方法和计算φ、a和q 的定量关系。如图所示,在洛仑兹力作用下,一个作匀速圆周运动的粒子,不论沿顺时针方向还是逆时针方向,从A点运动到B点,均具有三个重要特点。
在分析和解答带电粒子作匀速圆周运动的问题时,除了应熟悉上述基本规律之外,还必须掌握确定轨道圆心的基本方法和计算φ、a和q 的定量关系。如图所示,在洛仑兹力作用下,一个作匀速圆周运动的粒子,不论沿顺时针方向还是逆时针方向,从A点运动到B点,均具有三个重要特点。
(1)轨道圆心(O)总是位于A、B两点洛仑兹力(f)的交点上或AB弦的中垂线(OO¢)与任一个f的交点上。
(2)粒子的速度偏向角(),等于回旋角(a),并等于AB弦与切线的夹角--弦切角(q)的2倍,即 = a = 2q = w t。
(3)相对的弦切角(q)相等,与相邻的弦切角(q¢ )互补,即q + q¢ = 180°
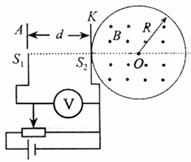 [例7]如图所示,所以O为圆心,R为半径的圆形区域内,有一个水平方向的匀强磁场,磁感应强度大小为B,方向垂直于纸面向外;竖直平行放置的极板A、K相距为d,AK之间的电压可以调节,S1、S2为A、K极板上的两个小孔,且S1、S2和O三点在垂直于极板的同一直线上,OS2=R;质量为m、电量为q的正离子从S1进入电场后,自S2射出并进入磁场区域,不计重力和离子进入电场时的初速度,问:
[例7]如图所示,所以O为圆心,R为半径的圆形区域内,有一个水平方向的匀强磁场,磁感应强度大小为B,方向垂直于纸面向外;竖直平行放置的极板A、K相距为d,AK之间的电压可以调节,S1、S2为A、K极板上的两个小孔,且S1、S2和O三点在垂直于极板的同一直线上,OS2=R;质量为m、电量为q的正离子从S1进入电场后,自S2射出并进入磁场区域,不计重力和离子进入电场时的初速度,问:
(1)为使正离子射出磁场时的速度的方向与进入时重直,A、K之间的电压应为多大?
(2)粒子在磁场中的运动时间多长?
[例7](1)U= ,(2)
,(2)
2、带电粒子在匀强磁场中做匀速圆周运动的几个基本公式
向心力公式: ,轨道半径公式:
,轨道半径公式: ,
,
周期公式: ,频率公式:
,频率公式: ,
,
角速度公式: ,动能公式:
,动能公式:
1、在不计带电粒子(如电子、质子、a粒子等基本粒子)的重力的条件下,带电粒子在匀强磁场的运动:
(1)若带电粒子的速度方向与磁场方向平行时,粒子不受洛仑兹力作用而作匀速直线运动。
(2)若粒子的速度方向与磁场方向垂直,则带电粒子在垂直于磁感线的平面内以入射速度v作匀速圆周运动,其运动所需的向心力全部由洛仑兹力提供。
(二)洛伦兹力
1.洛仑兹力的大小。
(1)洛仑兹力计算式为F=qvB,条件为磁场B与带电粒子运动的速度v垂直。
(2)当v∥B,F=0;当v⊥B,F最大。
2.洛仑兹力的方向。
(1)洛仑兹力的方向用左手定则判定:伸开左手,使大拇指和其余四指垂直,并且都跟手掌在同一平面内,把手放入磁场中,让磁感线垂直穿入掌心,四指指向正电荷的运动方向,那么,大拇指所指的方向就是正电荷所受洛仑兹力的方向;如果运动电荷为负电荷,则四指指向负电荷运动的反方向。
(2)F、v、B三者方向间的关系。已知v、B的方向,可以由左手定则确定F的唯一方向:F⊥v、F⊥B、则F垂直于v和B所构成的平面;但已知F和B的方向,不能唯一确定v的方向,由于v可以在v和B所确定的平面内与B成不为零的任意夹角,同理已知F和v的方向,也不能唯一确定B的方向。
3.洛仑兹力的特性
(1)安培力是大量运动电荷所受洛伦兹力的宏观表现。
(2)无论电荷的速度方向与磁场方向间的关系如何,洛仑兹力的方向永远与电荷的速度方向垂直,因此洛仑兹力只改变运动电荷的速度方向,不对运动电荷作功,也不改变运动电荷的速率和动能。所以运动电荷垂直磁感线进入匀强磁场仅受洛仑磁力作用时,一定作匀速圆周运动。
 (3)洛仑兹力是一个与运动状态有关的力,这与重力、电场力有较大的区别,在匀强电场中,电荷所受的电场力是一个恒力,但在匀强磁场中,若运动电荷的速度大小或方向发生改变,洛仑兹力是一个变力。
(3)洛仑兹力是一个与运动状态有关的力,这与重力、电场力有较大的区别,在匀强电场中,电荷所受的电场力是一个恒力,但在匀强磁场中,若运动电荷的速度大小或方向发生改变,洛仑兹力是一个变力。
[例5]每时每刻都有大量宇宙射线向地球射来,地磁场可以改变射线中大多数带电粒子的运动方向,使它们不能到达地面,这对地球上的生命有十分重要的意义。假设有一个带正电的宇宙射线粒子正垂直于地面向赤道射来,在地磁场的作用下,它将
A.向东偏转 B.向南偏转 C.向西偏转 D.向北偏转
[例5]A
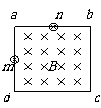 [例6]如图所示,边长为d的正方形区域abcd中充满匀强磁场,磁场大小为B,方向垂直纸面向里。一个氢核(质量为m,电量为e)从ad边的中点m沿着既垂直于ad边又垂直于磁场的方向,以一定速度射入磁场,正好从ab边的中点n射出磁场,则氢核射入磁场时的速度是____。现将磁场的磁感应强度变为原来的2倍,其他条件不变,则这个氢核经_____时间从磁场射出。
[例6]如图所示,边长为d的正方形区域abcd中充满匀强磁场,磁场大小为B,方向垂直纸面向里。一个氢核(质量为m,电量为e)从ad边的中点m沿着既垂直于ad边又垂直于磁场的方向,以一定速度射入磁场,正好从ab边的中点n射出磁场,则氢核射入磁场时的速度是____。现将磁场的磁感应强度变为原来的2倍,其他条件不变,则这个氢核经_____时间从磁场射出。
[例6]
(一)安培力
1.安培力的大小:
(1)安培力的计算公式:F=BIL,条件为磁场B与直导体L垂直。
(2)导体与磁场垂直时,安培力最大;当导体与磁场平行时,导体与磁场平行,安培力为零。
(3)F=BIL要求L上各点处磁感应强度相等,故该公式一般只适用于匀强磁场。
2.安培力的方向:
(1)安培力方向用左手定则判定:伸开左手,使大拇指和其余四指垂直,并且都跟手掌在同一个平面内,把手放入磁场中,让磁感线垂直穿入手心,并使伸开的四指指向电流方向,那么大拇指所指的方向就是通电导体在磁场中的受力方向。
(2)F、B、I三者间方向关系:已知B、I的方向(B、I不平行时),可用左手定则确定F的唯一方向:F⊥B,F⊥I,则F垂直于B和I所构成的平面,但已知F和B的方向,不能唯一确定I的方向。由于I可在图中平面α内与B成任意不为零的夹角。同理,已知F和I的方向也不能唯一确定B的方向。
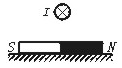 [例3]如右图所示,条形磁铁放在水平桌面上,在其正中间的上方固定一根长直导线,导线与磁铁垂直,给导线通以垂直纸面向里的电流,用FN表示磁铁对桌面的压力,用Fμ表示桌面对磁铁的摩擦力,电线中通电后(与通电前相比较)( )
[例3]如右图所示,条形磁铁放在水平桌面上,在其正中间的上方固定一根长直导线,导线与磁铁垂直,给导线通以垂直纸面向里的电流,用FN表示磁铁对桌面的压力,用Fμ表示桌面对磁铁的摩擦力,电线中通电后(与通电前相比较)( )
A.FN减小,Fμ=0 B.FN减小,Fμ≠0 C.FN增大,Fμ=0 D.FN增大,Fμ≠0
[例3]C
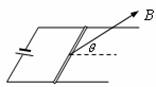 [例4]如图所示,一长L的直导线通以大小为I的电流,放在垂直于导线的磁感应强度为B的匀强磁场中,则导线所受安培力大小为
[例4]如图所示,一长L的直导线通以大小为I的电流,放在垂直于导线的磁感应强度为B的匀强磁场中,则导线所受安培力大小为
A.BLIsinθ B.BLIcosθ C.BLI/sinθ D.BLI
[例4]D
3.磁感应强度
(1)定义:在磁场中垂直于磁场方向的通电直导线,所受的安培力F跟电流I和导线长度L之乘积IL的比值叫做磁感应强度,
定义式为 。(条件是匀强磁场,或非匀强磁场中L很小,并且L⊥B )
。(条件是匀强磁场,或非匀强磁场中L很小,并且L⊥B )
磁感应强度是矢量,其方向就是磁场方向。
单位是特斯拉,符号为T,1T=1N/(Ažm)=1kg/(Ažs2)
(2)对定义式的理解:
①定义式中反映的F、B、I方向关系为:B⊥I,F⊥B,F⊥I,则F垂直于B和I所构成的平面。
②定义式可以用来量度磁场中某处磁感应强度,不决定该处磁场的强弱,磁场中某处磁感应强度的大小由磁场自身性质来决定。
③磁感应强度是矢量,其矢量方向是小磁针在该处的北极受力方向,与安培力方向是垂直的。
④如果空间某处磁场是由几个磁场共同激发的,则该点处合磁场(实际磁场)是几个分磁场的矢量和;某处合磁场可以依据问题求解的需要分解为两个分磁场;磁场的分解与合成必须遵循矢量运算法则。
[例1]有一小段通电导线,长为1cm,电流强度为5A,把它置于磁场中某点,受到的磁场力为0.1 N,则该点的磁感应强度B一定是
A.B=2 T B.B≤2 T C.B≥2 T D.以上情况都有可能
[例1]C
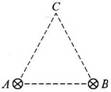 [例2]两根长直通电导线互相平行,电流方向相同,它们的截面处于等边△ABC的A和B处,如图所示.两通电导线在C处产生磁场的磁感应强度大小都是B0,则C处磁场的总磁感应强度大小是
[例2]两根长直通电导线互相平行,电流方向相同,它们的截面处于等边△ABC的A和B处,如图所示.两通电导线在C处产生磁场的磁感应强度大小都是B0,则C处磁场的总磁感应强度大小是
A.0 B.B0 C. D.2B0
D.2B0
[例2]C
2.地磁场的磁感线分布特点:
要明确三个问题:(磁极位置? 赤道处磁场特点?南北半球磁场方向?)
(1)地球是一个巨大的磁体、地磁的N极在地理的南极附近,地磁的S极在地理的北极附近;
(2)地磁场的分布和条形磁体磁场分布近似;
(3)在地球赤道平面上,地磁场方向都是由北向南且方向水平(平行于地面);
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com