
22.(本小题满分14分)
如图,已知椭圆 :
: 的焦点为
的焦点为 ,顶点为
,顶点为 ,离心率为
,离心率为 ,椭圆上的点到焦点的最短距离为1,过
,椭圆上的点到焦点的最短距离为1,过 的直线
的直线 交椭圆
交椭圆 于
于 两点,点
两点,点 在
在 轴的上方,且
轴的上方,且 。
。
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)求以 为圆心、
为圆心、 为半径的圆
为半径的圆 的方程;
的方程;
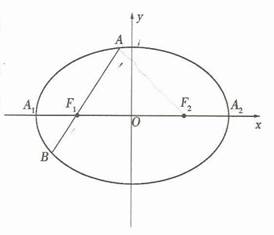 (Ⅲ)设
(Ⅲ)设 关于
关于 轴的对称点为
轴的对称点为 ,椭圆
,椭圆 在直线
在直线 左侧的部分(包括端点)与圆
左侧的部分(包括端点)与圆 在直线
在直线 右侧的部分合成封闭曲线
右侧的部分合成封闭曲线 ,过
,过 的直线
的直线 与曲线
与曲线 交于
交于 两点,求
两点,求 的取值范围
的取值范围
21.(本小题满分12分)
已知函数 。
。
(Ⅰ)若函数 在点
在点 处切线的倾斜角为
处切线的倾斜角为 ,求实数
,求实数 的值;
的值;
(Ⅱ)若函数 在区间
在区间 上为单调递增函数,求实数
上为单调递增函数,求实数 的取值范围;
的取值范围;
(Ⅲ)在(Ⅱ)的条件下,记 的取值范围为集合
的取值范围为集合 ,对任意
,对任意 ,若
,若 是函数
是函数 的极大值点,求
的极大值点,求 ,并直接写出
,并直接写出 的最大值
的最大值
20.(本小题满分12分)
如图,为测量鼓浪屿郑成功雕像 的高度及取景点
的高度及取景点 与
与 之间的距离(点
之间的距离(点 在同一水平面上,雕像垂直该水平面于点
在同一水平面上,雕像垂直该水平面于点 ,且
,且 三点共线),某校研究性学习小组同学在
三点共线),某校研究性学习小组同学在 三点处测得顶点
三点处测得顶点 的仰角分别为45°、30°、
的仰角分别为45°、30°、
30°, =60°,
=60°, =
= 米
米
 (Ⅰ)求雕像
(Ⅰ)求雕像 的高度;
的高度;
(Ⅱ)求取景点 与
与 之间的距离。
之间的距离。
19.(本小题满分12分)
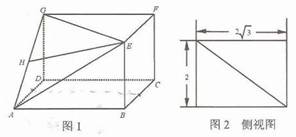
图l是长方体截去一个角后得到的几何体,其中底面 是正方形,
是正方形, 为
为 中点,图2是该几何体的侧视图。
中点,图2是该几何体的侧视图。
(Ⅰ)求四棱锥 的体积;
的体积;
(Ⅱ)判断直线 与平面
与平面 的位置关系,并给予证明;
的位置关系,并给予证明;
(Ⅲ)正方形 内(包括边界)是否存在点
内(包括边界)是否存在点 ,使三棱锥
,使三棱锥 体积是四棱锥
体积是四棱锥 体积的
体积的 ?若存在,请指出满足要求的点
?若存在,请指出满足要求的点 的轨迹,并在图中画出轨迹图形;若不存在,请说明理由
的轨迹,并在图中画出轨迹图形;若不存在,请说明理由
18.(本小题满分12分)
已知函数 (
( 为常数)
为常数)
(Ⅰ)若点 都在函数
都在函数 的图象上,证明:数列
的图象上,证明:数列 为等差数
为等差数
列;
(Ⅱ)若点 在函数
在函数 的图象上,求数列
的图象上,求数列 的前
的前 项和
项和
17.(本小题满分12分)
某城市对一项惠民市政工程满意程度(分值:0-100分)进行网上调查,有18000位市民参加了投票,经统计,各分数段的人数如下表:
|
满意程度 (分数) |
[0,20) |
[20,40) |
[40,60) |
[60,80) |
[80,100) |
|
人数 |
1800 |
2880 |
3600 |
5400 |
4320 |
现用分层抽样的方法从所有参与网上投票的市民中随机抽取 位市民召开座谈会,其中满意程度在[0,20]的有5人
位市民召开座谈会,其中满意程度在[0,20]的有5人
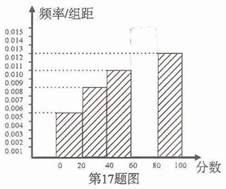
(Ⅰ)求 的值,并补充完整右边的频率分布直方图;
的值,并补充完整右边的频率分布直方图;
(Ⅱ)若满意程度在[0,20]的5人中恰有2位为女性,座谈会将从这5位市民中任选两位发言,求至少有一位女性市民被选中的概率。
16.有14个小球,将它们任意分成三堆,求出这三堆小球球数的乘积;再将其中一堆小球任意分成三堆,求出这三堆小球球数的乘积,……,如此下去,直到不能再分为止。则所有这些乘积之和的最大值为
15.已知等比数列 的前
的前 项积为
项积为 ,若
,若 ,
, ,则
,则 。
。
14.已知实数 满足条件
满足条件 ,则
,则 的最小值 。
的最小值 。
13.已知 ,
, ,
, ,则
,则
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com