
21.解:(1)
因为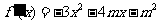 , 所以
, 所以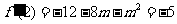 …2分
…2分
解得m=-1或m=-7(舍),即m=-1 …3分
(2)由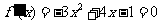 ,解得
,解得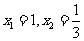 ……………4分
……………4分
列表如下:
|
x |
0 |
(0,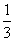 ) ) |
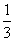 |
(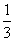 ,1) ,1) |
1 |
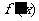 |
|
- |
|
+ |
|
|
f(x) |
2 |
↘ |
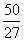 |
↗ |
2 |
所以函数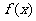 在区间[0,1]的最小值为
在区间[0,1]的最小值为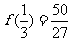 …7分
…7分
(3)因为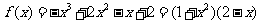
由(2)知,当x∈[0,1]时, 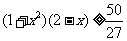 ,所以
,所以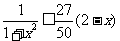 ,
,
所以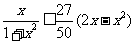 …9分
…9分
当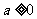 ,
,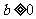 ,
,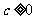 ,且
,且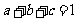 时,
时,
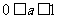 ,
,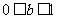 ,
, ,
,
所以
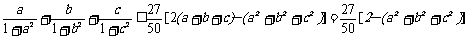 …10分
…10分
又因为
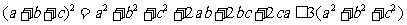 ,
,
所以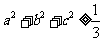 …11分
…11分
故 (当且仅当
(当且仅当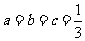 时取等号) …12分
时取等号) …12分
20. (1)由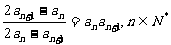 可得
可得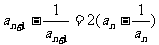 …3分
…3分
又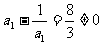 …4分
…4分
所以数列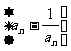 是等比数列; …5分
是等比数列; …5分
(2)由(1)有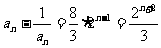
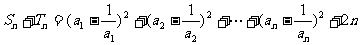
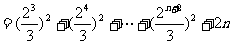
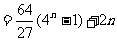
要使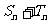 为整数,需
为整数,需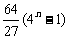 为整数,
为整数,
当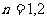 时,不满足;
时,不满足;
当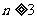 时
时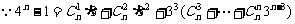
需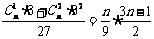 为整数,故n为9的倍数,
为整数,故n为9的倍数,
所以当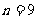 时,
时,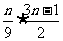 为整数,故最小的正整数n为9.
为整数,故最小的正整数n为9.
19.(1)记事件A为“任取两张卡片,将卡片上的函数相加得到的函数是奇函数”,由题意知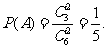 …4分
…4分
(2),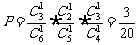 …8分
…8分
18.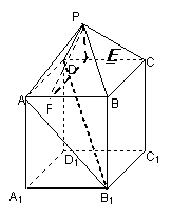 (Ⅰ)证明:
(Ⅰ)证明:
因为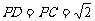 ,
,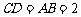 ,所以
,所以 为等腰直角三角形,所以
为等腰直角三角形,所以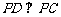 .
……1分
.
……1分
因为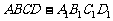 是一个长方体,所以
是一个长方体,所以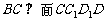 ,而
,而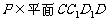 ,所以
,所以 ,所以
,所以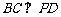 . …3分
. …3分
因为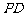 垂直于平面
垂直于平面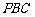 内的两条相交直线
内的两条相交直线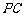 和
和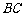 ,由线面垂直的判定定理,可得
,由线面垂直的判定定理,可得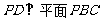 .…4分
.…4分
(Ⅱ)解:过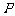 点在平面
点在平面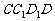 作
作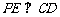 于
于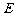 ,取
,取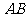 的中点F连接
的中点F连接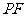 .…5分
.…5分
则所以 就是所求二面角的平面角.……6分
就是所求二面角的平面角.……6分
因为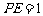 ,
, ,,所以
,,所以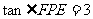 . …8分
. …8分
(Ⅲ)解:当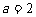 时,
时,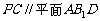 .
…9分
.
…9分
当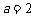 时,四边形
时,四边形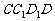 是一个正方形,所以
是一个正方形,所以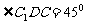 ,而
,而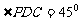 ,所以
,所以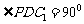 ,所以
,所以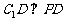 .
…10分
.
…10分
而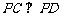 ,
,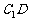 与
与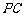 在同一个平面内,所以
在同一个平面内,所以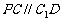 . …11分
. …11分
而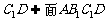 ,所以
,所以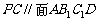 ,所以
,所以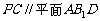 。…12分
。…12分
17.(1)由已知可得 ……3分
……3分
由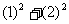 得
得 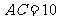 ……5分
……5分
(2)由上可得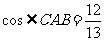 ,又
,又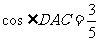 ,所以可得
,所以可得
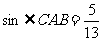 ,
,
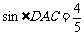 ……7分
……7分
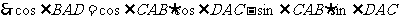
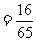 ……10分
……10分
13. 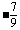 ; 14. -3;
15. 4; 16. 16:1.
; 14. -3;
15. 4; 16. 16:1.
22.有如下结论:“圆 上一点
上一点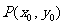 处的切线方程为
处的切线方程为 ”,类比也有结论:“椭圆
”,类比也有结论:“椭圆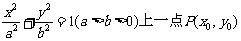 处的切线方程为
处的切线方程为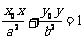 ”,过椭圆C:
”,过椭圆C: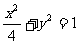 的右准线l上任意一点M引椭圆C的两条切线,切点为 A、B.
的右准线l上任意一点M引椭圆C的两条切线,切点为 A、B.
(1)求证:直线AB恒过一定点;
(2)当点M的纵坐标为1时,求△ABM的面积.
数学(文):
21、设函数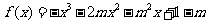 (其中
(其中 )的图象在
)的图象在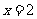 处的切线与直线
处的切线与直线 平行.
平行.
(1)求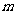 的值;
的值;
(2)求函数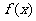 在区间[0,1]的最小值;
在区间[0,1]的最小值;
(3)若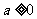 ,
,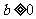 ,
,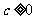 ,且
,且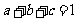 ,试根据上述(1)、(2)的结论证明:
,试根据上述(1)、(2)的结论证明: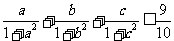 .
.
20.已知各项均为正数的数列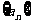 满足:
满足: ,且
,且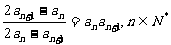 .
.
(1)求证:数列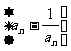 是等比数列;
是等比数列;
(2)设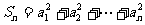 ,
,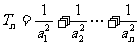 ,求
,求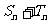 ,并确定最小的正整数n,使
,并确定最小的正整数n,使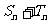 为整数.
为整数.
19.一个盒子装有六张卡片,上面分别写着如下六个定义域为R的函数:f1(x)=x,f2(x)=x2,f3(x)=x3,f4(x)=sinx,f5(x)=cosx,f6(x)=2.
(1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;
(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片则停止抽取,否则继续进行,求恰好抽取了3次卡片的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com