
18、考查等差数列概念及求和,函数基本知识. 以及化归的数学思想。
解(Ⅰ)∵f(x-1)=(x-1-1)2-4=(x-2)2-4 ………..2分
∴f(x)=(x-1)2-4,
∴a1=(x-2)2-4,a3=(x-1)2-4 ………………………4 分
又a1+a3=2a2,解得x=0或x=3. ……………………6分
(Ⅱ)∵a1、a2、a3分别为0、-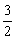 、-3或-3、-
、-3或-3、-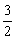 、0
、0
∴an=-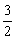 (n-1)或an=
(n-1)或an=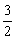 (n-3)
.9分
(n-3)
.9分
①当an=-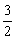 (n-1)时,a2+a5+…+a26=
(n-1)时,a2+a5+…+a26=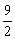 (a2+a26)=
(a2+a26)=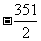 ….11分
….11分
②当an=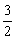 (n-3)时,a2+a5+…+a26=
(n-3)时,a2+a5+…+a26=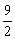 (a2+a26)=
(a2+a26)=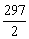 . 13分
. 13分
15、(Ⅰ)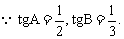
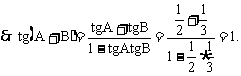 4分
4分
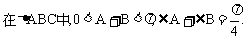 5分
5分
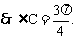 6分
6分
(Ⅱ)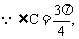 ∴ ∠C所对的边最长,∠B所对的边最短,
7分
∴ ∠C所对的边最长,∠B所对的边最短,
7分
由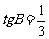 ,求得
,求得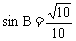 ,
9分
,
9分
由正弦定理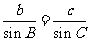

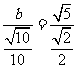
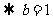 13分
13分
(16)(本大题满分13分)
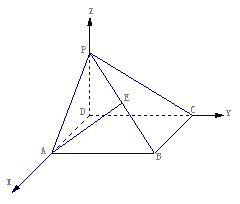 解:(Ⅰ)以DA、DC、DP所在直线分别为x轴、y轴、z轴建立空间直角坐标系,
解:(Ⅰ)以DA、DC、DP所在直线分别为x轴、y轴、z轴建立空间直角坐标系,
如图示:则A(2,0,0),B(2,2,0),C(0,2,0),…1分
设P(0,0,2m)(m>0),则E(1,1,m), …2分
∴ 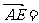 (-1,1,m),
(-1,1,m),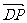 =(0,0,2m)…3分
=(0,0,2m)…3分
∴ 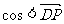 ,
,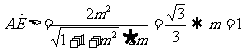 ,…5分
,…5分
∴ 点E坐标是(1,1,1) ……………………………… 6分
(Ⅱ)∵ 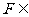 平面PAD, ∴ 可设F(x,0,z)
平面PAD, ∴ 可设F(x,0,z)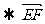 =(x-1,-1,z-1),7分
=(x-1,-1,z-1),7分
要使 EF⊥平面PCB ,则须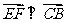 ,且
,且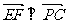 … 8分
… 8分
即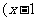 ,-1,
,-1,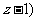
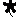 2,0,
2,0,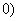 =0, 且
=0, 且 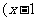 ,-1,
,-1,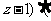 0,2,-2)=0, 10分
0,2,-2)=0, 10分
解得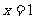 ,
, 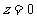 …………………………………12分
…………………………………12分
∴ 存在点F(1,0,0),即点F是AD的中点时,EF⊥平面PCB。 13分
(17)(本题满分13分)
解:(I)该事件为5次独立重复试验发生3次或4次或5次……………………1分
∴P=P5(3)+P5(4)+P5(5) …………………………………3分
=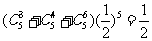 …………………………………………6分
…………………………………………6分
(II)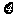 的可能取值分别为1,2,3,4,5. ………7分
的可能取值分别为1,2,3,4,5. ………7分
分布列如下:
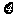 |
1 |
2 |
3 |
4 |
5 |
|
P |
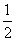 |
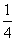 |
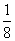 |
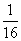 |
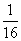 |
…11分
∴ E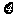 =
=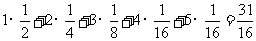 ……………13分
……………13分
14. 9500
13、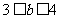 提示:由
提示:由 在
在 内恒为非负,求出
内恒为非负,求出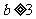 ,再由
,再由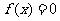 解得
解得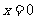 或
或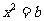 ,
,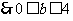 ,
,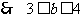 。
。
12、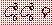 400 0.25 提示:P=
400 0.25 提示:P=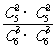
11、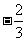 提示:
提示: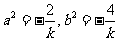
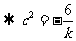 ,从而
,从而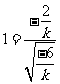 ,解得
,解得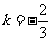 .
.
10、C 提示:令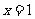 得
得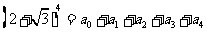 ,令
,令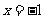 得
得 ,两式相乘得
,两式相乘得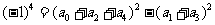
9、B 提示:∵f(x)在(-2,+∞)上是增函数,在(-∞,-2)上是减函数,∴f(x)的对称轴方程为x=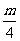 =-2,∴m=-8.这时f(x)=2x2+8x+3,∴f(1)=13.故选B.
=-2,∴m=-8.这时f(x)=2x2+8x+3,∴f(1)=13.故选B.
8、D
7、C 提示:作CD⊥AB于D,作C1D1⊥A1B1于D1,连B1D、AD1,易知ADB1D1是平行四边形,由三垂线定理得A1B⊥AC1,选C。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com