
8.从4名教师与5名学生中任选3人,其中至少要有教师与学生各1人,则不同的选法共有 ( )
A.140种 B.80种 C.70种 D.35种
7.关于函数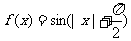 有下列判断:①是偶函数;②是奇函数;③是周期函数;④不是周期函数,其中正确的是 ( )
有下列判断:①是偶函数;②是奇函数;③是周期函数;④不是周期函数,其中正确的是 ( )
A.①与④ B.①与③ C.②与④ D.②与③
6.函数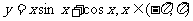 的单调增区间是 ( )
的单调增区间是 ( )
A.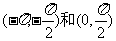 B.(-
B.(-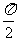 ,0)和(0,
,0)和(0,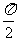 )
)
C.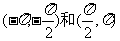 D.(-
D.(-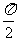 ,0)和(
,0)和(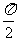 ,
, )
)
5.设x,y满足约束条件: 的最大值与最小值分别为 ( )
的最大值与最小值分别为 ( )
A.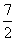 ,3 B.5,
,3 B.5,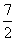 C.5,3 D.4,3
C.5,3 D.4,3
4.设a、b表示直线,α、β表示平面,α//β的充分条件是 ( )
A.a//b,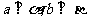 B.
B.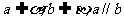
C.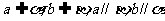 D.
D.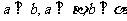
3.已知|a|=1,|b|=2,a=λb(λ∈R),则|a-b|= ( )
A.1 B.3 C.1或3 D.|λ|
2.抛物线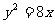 上的点
上的点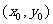 到抛物线焦点的距离为3,则|y0|= ( )
到抛物线焦点的距离为3,则|y0|= ( )
A.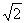 B.2
B.2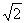 C.2 D.4
C.2 D.4
1.设全集U={1,2,3,4,5},集合A={1,2,3},集合B={3,4,5},则(CUA)∪(CUB)=
( )
A.{1,2,3,4,5} B.{3}
C.{1,2,4,5} D.{1,5}
20.解:本题考查向量与解析几何的综合应用。
(Ⅰ)由已知,得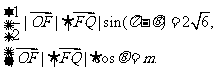 2分
2分
∴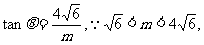 5分
5分
∴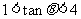 ,则
,则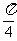
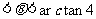 7分
7分
(Ⅱ)设所求的双曲线方程为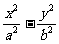 =1,(a>0,b>0),Q(x1,y1),则
=1,(a>0,b>0),Q(x1,y1),则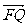 =(x1-c,y1)
=(x1-c,y1)
∵△OFQ的面积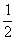 |
|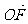 ||y1|=2
||y1|=2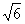 ,∴y1=±
,∴y1=±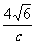 ,
,
又由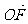 ·
·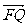 =(c,0)·(x1-c,y1)=(x1-c)c=(
=(c,0)·(x1-c,y1)=(x1-c)c=(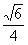 -1)c2,∴x1=
-1)c2,∴x1=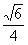 c,
10分
c,
10分
|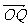 |=
|=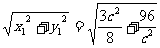 ≥
≥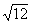 ,当且仅当c=4时,|
,当且仅当c=4时,|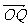 |最小.
|最小.
此时Q的坐标为(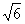 ,
,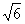 ),或(
),或(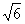 ,-
,-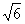 ).由此可得
).由此可得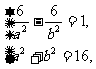
解得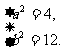 14分
14分
故所求方程为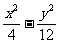 =1. 15分
=1. 15分
19. 本题考查导数的应用以及逻辑推理能力。
(Ⅰ) 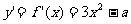 ,
,
若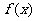 在
在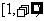 上是单调递减函数,则须
上是单调递减函数,则须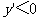 ,即
,即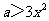 ,这样的实数
,这样的实数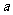 不存在,
不存在,
故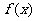 在
在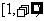 上不可能是单调递减函数.
…
4分.
上不可能是单调递减函数.
…
4分.
(Ⅱ) 若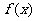 在
在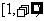 上是单调递增函数,则
上是单调递增函数,则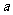 ≤
≤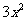 ,
,
由于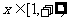 ,故
,故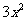 ≥3.
≥3.
从而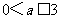 .8分
.8分
(Ⅲ) 由(Ⅰ)、(Ⅱ)可知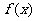 在
在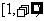 上只能为单调增函数,
上只能为单调增函数,
若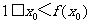 ,则
,则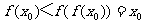 矛盾,
.10分
矛盾,
.10分
若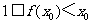 ,则
,则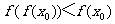 ,即
,即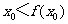 矛盾,
矛盾,
故只有 成立.
..13分
成立.
..13分
证法二:设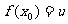 ,则
,则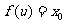 ,∴
,∴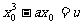 ,
, 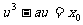 ,
,
两式相减得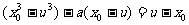
∴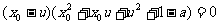 ,
,
∵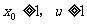
∴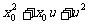 ≥3,又
≥3,又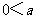 ≤3,∴
≤3,∴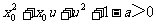
∴ ,即
,即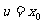 ,亦即
,亦即 ,证毕.
,证毕.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com