
14.(2010福建卷)《朱子语类》云:“唐制:每事先经由中书省,中书做定将上,得旨,再下中书,中书以付门下。或存未当,则门下缴驳,……若可行,门下又下尚书省,尚书但主书撰奉行而已。”对此理解有误的是
A.体现三省分权制 B.完善中央监察机制
C.减少行政决策失误 D.分做相权加强皇权
[答案]B。
[解析]此题考查三省六部制概念的掌握,显然根据材料和概念的理解,ABC均是正确的。B选项转换换了概念,它不属于监察范畴。
13.(2010福建卷)表2中的日文写法主要仿自中国某种书法字体。唐代擅长这一书体的书法家是

A.王羲之 B.颜真卿 C.柳公权 D.怀素
[答案]D。
[解析]此题考查古代书法艺术和书法名家。解法一:日本文字主要由吉备真备利用汉字创造的片假名和学问僧空海采用汉字草书创造的平假名构成,材料中点出平假名,故受草书影响,怀素是狂草名家,选D;解法二:根据材料中的平假名字体判断是模仿草书,这是本题考查的主要意图;解法三:排除法,王羲之非唐朝,颜真卿和刘公权擅长楷体,故选D。
21、(1)(矩阵变换)[解析](1) ,对应系数有
,对应系数有 ;(2)取
;(2)取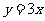 上一点
上一点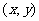 ,设经过变换后对应点为
,设经过变换后对应点为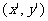 ,则
,则 ,从而
,从而 ,所以经过变换后的图像方程为
,所以经过变换后的图像方程为 。
。
[命题意图]本题考查的是学生对矩阵运算理解与掌握,要求考生能够正确进行运算,熟悉矩阵的基本运算方法。
[点评]本题相对基础,对于学生提高自信心有一定帮助。
(2)(坐标系与参数方程)[解析](1)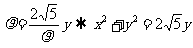 ,所以
,所以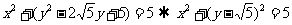 ;(2)直线的一
;(2)直线的一 般方程为
般方程为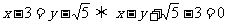 ,容易知道P在直线上,又
,容易知道P在直线上,又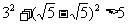 ,所以P在圆外,联立圆与直线方程可以得到:
,所以P在圆外,联立圆与直线方程可以得到: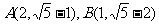 ,所以|PA|+|
,所以|PA|+| PB|=|AB|+2|PA|=
PB|=|AB|+2|PA|=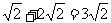 ,所以答案为
,所以答案为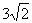
[命题意图]本题考查了学生极坐标方程化一般方程、参数方程化一般方程的能力以及综合的分析问题能力,有一定的选拔意义。
[ 点评]遇到参数方程题目的时候,只需要化简为一般方程,问题便迎刃而解。
点评]遇到参数方程题目的时候,只需要化简为一般方程,问题便迎刃而解。
 (3)(不等式选讲)[解析]
(3)(不等式选讲)[解析] ,对应系数得a=2;(2)
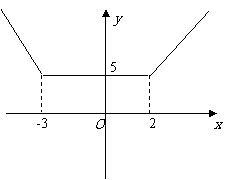
,对应系数得a=2;(2)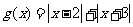 的图像为
的图像为
所以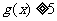 ,故
,故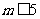 。
。
[命题意图]本题考查学生解不等式的基本能力,难度较低。
[点评]本类型的方法是绘图法,或者采用零点分区间法,考查基本。
20、[解析](1) ,令
,令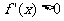 得到
得到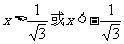 ,令
,令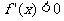 有
有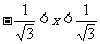 ,因此原函数的单调递增区间为
,因此原函数的单调递增区间为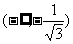 和
和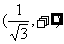 ;单调递减区间为
;单调递减区间为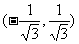
(2)(i)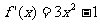 ,
, ,
,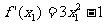 ,因此过点
,因此过点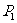 的切线方程为:
的切线方程为: (ii)[命题]若对于任意函数
(ii)[命题]若对于任意函数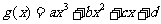 的图像为曲线
的图像为曲线 ,其类似于(2)(i)的命题为:若对任意不等于
,其类似于(2)(i)的命题为:若对任意不等于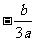 的实数
的实数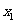 ,曲线与其在点
,曲线与其在点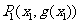 处的切线交于另一点
处的切线交于另一点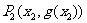 ,曲线
,曲线 与其在点
与其在点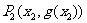 处的切线交于另外一点
处的切线交于另外一点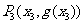 ,线段
,线段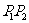 、
、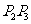 与曲线
与曲线 所围成面积为
所围成面积为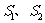 ,则
,则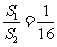 。
。
[证明]对于曲线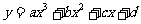 ,无论如何平移,其面积值是恒定的,所以这里仅考虑
,无论如何平移,其面积值是恒定的,所以这里仅考虑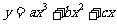 的情形,
的情形,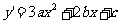 ,
,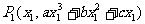 ,
,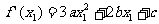 ,因此过点
,因此过点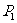 的切线方程为:
的切线方程为:
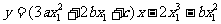 ,联立
,联立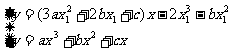 ,得到:
,得到: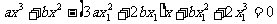 ,
,
化简:得到
从而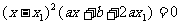 所以
所以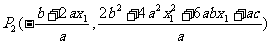 同样运用(i)中方法便可以得到
同样运用(i)中方法便可以得到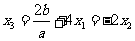
所以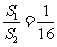
[命题意图]本题从函数角度出发,考查了积分运算、单调性、求导等基本能力,又综合地考查了学生分析问题、解决问题的能力。计算量较大,不容易正确。
[点评]该题思维量较小,计算量却较为庞大,对考生有一定的区分作用。
19、[解析](1)为使小艇航行距离最短,理想化的航行路线为OT,小艇到达T位置时轮船的航行位移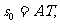 即
即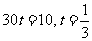 ,
,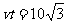 ,从而
,从而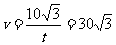 (海里/时)
(海里/时)
(2)讨论:(1)若轮船与小艇在A、T之间G位置相遇时,根据小艇的速度限制,有OG<AG,但实际上,这种情况中AG<OG,所以不符合要求舍去。轮船与小艇的交点必在T、B之间。
(2)若轮船与小艇在H处相遇时,在直角三角形OHT中运用勾股定理有: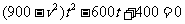 ,等价于
,等价于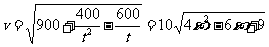
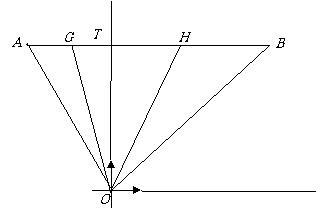 从而
从而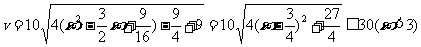
所以当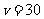 时,
时,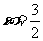 ,
,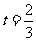
也就是说,当小艇以30海里每小时的速度,沿北偏东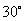 方向行走能以最短的时间遇到轮船。
方向行走能以最短的时间遇到轮船。
[命题意图]本题从三角函数出发,考查了学生运用知识解决实际问题的能力、求解一元二次方程最值问题的能力以及综合分析问题的能力。
[点评]对待应用题没有什么通解通法,只要你不畏惧困难,认真读题、审题,通过列表、作图等方式合理分析已知量间的关系,总是能够轻松解题。
16、[解析](1)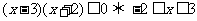 ,则
,则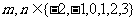
 有
有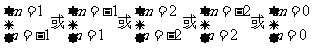 ,因此A包含的基本事件为:
,因此A包含的基本事件为: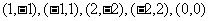
(2)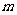 的可能去取为
的可能去取为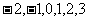 ,则
,则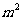 的可能取值为
的可能取值为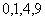
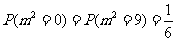 ,
,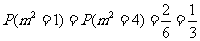
因此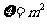 得分布列为:
得分布列为:
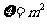 |
0 |
1 |
4 |
9 |
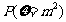 |
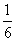 |
 |
 |
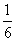 |
数学期望为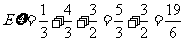

[命题意图]本题考查学生对概率分布的理解以及数学期望的计算,难度较易。
[点评]本题作为解答题的第一题具备送分的作用,考生只要掌握了基本的计算知识,能够轻松应对。
(ii)过O点做OT平行于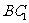 ,则由
,则由 有
有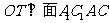 ,所以
,所以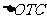 即为面
即为面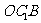 在
在 内的投影,设
内的投影,设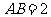 ,则
,则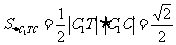 ,设二面角
,设二面角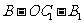 的平面角大小为
的平面角大小为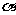 ,则
,则
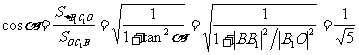
从而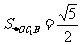 ,故
,故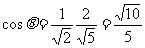
[命题意图]本题从棱柱出发,综合地考查了学生线面垂直、面面垂直的证明方法以及二面角、简单概率的求解,综合性强,灵活度大,是一道较好的题目。
[点评]在完成立体几何题目时,考生应当尽量把握从已知到未知的推理,发挥自己的空间思维能力,转化图形。正确求解。
11、[答案]124
[命题意图]本题通过抽象函数,考查了函数的周期性,单调性,以及学生的综合分析能力,难度不大。
[解析]1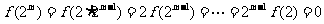 ,正确;2取
,正确;2取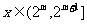 ,则
,则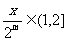 ;
;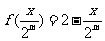 ,从而
,从而
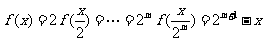 ,其中,
,其中,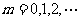 ,从而
,从而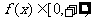 ,正确;3
,正确;3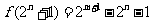 ,假设存在
,假设存在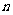 使
使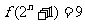 ,即存在
,即存在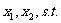
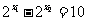 ,又,
,又,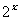 变化如下:2,4,8,16,32,……,显然不存在,所以该命题错误;4根据前面的分析容易知道该选项正确;综合有正确的序号是124
变化如下:2,4,8,16,32,……,显然不存在,所以该命题错误;4根据前面的分析容易知道该选项正确;综合有正确的序号是124
6、[答案]D
[命题意图]本题考查考生对立体几何体的理解程度、空间想像能力。灵活,全面地考查了考生对知识的理解。
[解析]若FG不平行于EH,则FG与EH相交,焦点必 然在B1C1上,而EH平行于B1C1,矛盾,所以FG平行于EH;由
然在B1C1上,而EH平行于B1C1,矛盾,所以FG平行于EH;由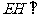 面
面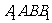 ,得到
,得到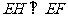 ,可以得到四边形EFGH为矩形,将
,可以得到四边形EFGH为矩形,将 从正面看过去,就知道是一个五棱柱,C正确;D没能正确理解棱台与这个图形。
从正面看过去,就知道是一个五棱柱,C正确;D没能正确理解棱台与这个图形。
 [答案]C
[答案]C
[命题意图]本题从大学数列极限定义的角度出发,仿造构造了分渐近线函数,目的是考查学生分析问题、解决问题的能力,考生需要抓住本质:存在分渐近线的充要条件是 时,
时,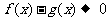 进行做答,是一道好题,思维灵活。
进行做答,是一道好题,思维灵活。
[解析]要透过现象看本质,存在分渐近线的充要条件是 时,
时,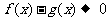 。对于1,当
。对于1,当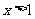 时便不符合,所以1不存在;对于2,肯
时便不符合,所以1不存在;对于2,肯 定存在分渐近线,因为当时,
定存在分渐近线,因为当时,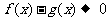 ;对于3,
;对于3,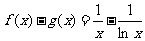 ,设
,设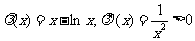 且
且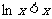 ,所以当
,所以当 时
时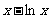 越来愈大,从而
越来愈大,从而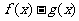 会越来越小,不会趋近于0,所以不存在分渐近线;4当
会越来越小,不会趋近于0,所以不存在分渐近线;4当 时,
时,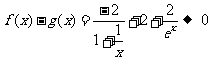 ,因此存在分渐近线。故,存在分
,因此存在分渐近线。故,存在分 渐近线的是24选C
渐近线的是24选C

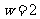 ,得到
,得到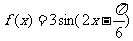 ,当
,当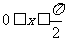 时,
时,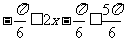 ,所以
,所以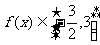
5、[答案]C
[命题意图]本题考查学生对程序框图的理解。选材较为简单,只需要考生能从上到下一步步列出就可以正确作答。
[ 解析]s=0
解析]s=0 i=1
i=1 a=2
a=2
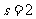

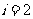



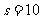

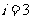

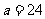

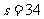
 i=4
i=4 输出i=4,选择C
输出i=4,选择C
4、[答案]C
[命题意图]本题从分段函数的角度出发,考查了学生对基本初等函数的掌握程度。
[解析]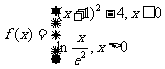 ,绘制出图像大致为
,绘制出图像大致为
所以零点个数为2。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com