
3.下列各句中加点的词语最恰当的一项是(3分)
A.几家上市公司的倒闭,引发了股市的大幅振荡;证监会对此予以高度关注。
B.最让我敬佩的是老人的人品,他胸无城府,朴实无华,心灵如蓝天一样透明,在今天这个功利浮躁的年代里,这种说真话、做真人的品质实在是难能可贵。
C.经过西方现代、后现代美学思潮熏陶的新生代作家,文学观念已经和他们的前辈南辕北辙。
D.他工作认真负责,勤勤恳恳 ,不管他从事的事业重要和不重要,都不失为一个值得赞扬的人物。
2.下列词语中,错别字最多的一项是(3分)
A.精萃 白内瘴 要言不繁 百尺杆头,更进一步
B.欠收 爆冷门 渊远流长 言必信,行必果
C.通牒 绵里针 盘根错结 机不可失,失不再来
D.炫丽 殊不知 见风驶舵 城门失火,殃及池鱼
1.下列词语中加点的字,每对读音都不相同的一组是(3分) w_w*w.k*s 5*
A.长相/相机行事 积攒/攒三聚五 纰缪/媲美 巷子/巷道
B.包扎/安营扎寨 咯血/恪尽职守 沮丧/龃龉 提防/堤堰
C.模样/模棱两可 泄露/公开露面 间距/信笺 沏茶/堆砌
D.畜养/畜牲 艾草/自怨自艾 果脯/哺育 颤动/ 打颤
20.(1)由已知 ,
,
 ,得
,得



由数列 是等差数列,得
是等差数列,得


所以,
 ,
, ,得
,得 .………………………5分
.………………………5分
(2)由 ,可得
,可得


且当 时,
时,

所以,当 时,
时,

 ,………………………4分
,………………………4分
因此,数列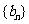 是一个公比为
是一个公比为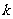 的等比数列.…………………………………………1分
的等比数列.…………………………………………1分
(3)解答一:写出必要条件,如,由(1)知,当 时,数列
时,数列 是等差数列,
是等差数列,
所以 是数列
是数列 为等比数列的必要条件. ………………………………3分
为等比数列的必要条件. ………………………………3分
解答二:写出充分条件,如 或
或 等,并证明 ……………… 5分
等,并证明 ……………… 5分
解答三: 是等比数列的充要条件是
是等比数列的充要条件是
 ……………………2分
……………………2分
充分性证明:
若
 ,则由已知
,则由已知 ,
,
 得
得


所以, 是等比数列.……………………………………………………………2分
是等比数列.……………………………………………………………2分
必要性证明:若 是等比数列,由(2)知,
是等比数列,由(2)知,


 ,
,
 . …………………………………………1分
. …………………………………………1分
当 时,
时,
 .
.
上式对 也成立,所以,数列
也成立,所以,数列 的通项公式为:
的通项公式为:

 .
.
所以,当 时,数列
时,数列 是以
是以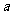 为首项,
为首项, 为公差的等差数列.
为公差的等差数列.
所以, .……………………………………………………………………1分
.……………………………………………………………………1分
当 时,
时,
 .
.
上式对 也成立,所以,
也成立,所以,

 ……………………1分
……………………1分
所以,
 . …………………………………………1分
. …………………………………………1分
即,等式 对于任意实数
对于任意实数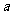 均成立.
均成立.
所以,
 .……………………………………………………………1分
.……………………………………………………………1分
19.(1)方法一:如图,以线段 的中点为原点
的中点为原点 ,
,
 以线段
以线段 所在的直线为
所在的直线为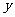 轴建立直角坐标系
轴建立直角坐标系 .
.
则, .
……………………………2分
.
……………………………2分
设动点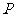 的坐标为
的坐标为 ,则动点
,则动点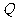 的坐标为
的坐标为
 ,
, , …………2分
, …………2分
由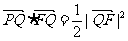 ,得
,得 ,…2分
,…2分
方法二:由 得,
得, .…………………………2分
.…………………………2分
所以,动点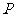 的轨迹
的轨迹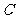 是抛物线,以线段
是抛物线,以线段 的中点
的中点
为原点 ,以线段
,以线段 所在的直线为
所在的直线为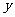 轴建立直角坐标系
轴建立直角坐标系 ,可得轨迹
,可得轨迹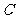 的方程为:
的方程为: .…………………………………………………………4分
.…………………………………………………………4分
(2)方法一:如图,设直线 的方程为
的方程为 ,
, ,
, ,……1分
,……1分
则 . ……………………………………………………………………………1分
. ……………………………………………………………………………1分
联立方程组 消去
消去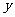 得,
得,
 ,
, ,故 …………………………………………1分
,故 …………………………………………1分
 ……………………………………………………………………………1分
……………………………………………………………………………1分
由 ,
,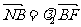 得,
得,
 ,
, ,……………………………………………………2分
,……………………………………………………2分
整理得, ,
, ,
,
 .…………………4分
.…………………4分
方法二:由已知 ,
,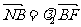 ,得
,得 .
…………………2分
.
…………………2分
于是, , ① …………………………………………………3分
, ① …………………………………………………3分
如图,过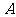 、
、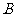 两点分别作准线
两点分别作准线 的垂线,垂足分别为
的垂线,垂足分别为 、
、 ,
,
则有 ② …………………………………………………3分
② …………………………………………………3分
由①,②得 .…………………………………………………………………2分
.…………………………………………………………………2分
18.(1)设从今年起的第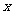 年(今年为第1年)该企业人均发放年终奖为
年(今年为第1年)该企业人均发放年终奖为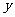 万元.则
万元.则
 ; ………………………………………4分
; ………………………………………4分
解法一:由题意,有 ,…………………………………………1分
,…………………………………………1分
解得, .………………………………………………………………1分
.………………………………………………………………1分
所以,该企业在10年内不能实现人均至少3万元年终奖的目标.……………1分
解法二:由于 ,所以
,所以 …2分
…2分
所以,该企业在10年内不能实现人均至少3万元年终奖的目标.……………1分
(2)解法一:设 ,则
,则


 ,………………………………4分
,………………………………4分
所以, ,得
,得 . ………………………………………2分
. ………………………………………2分
所以,为使人均发放的年终奖年年有增长,该企业员工每年的净增量不能超过23人.
……………………………………………………………………………………1分
解法二:
……………………………………………………………………………………4分
由题意,得 ,解得
,解得 . ……………………………2分
. ……………………………2分
所以,为使人均发放的年终奖年年有增长,该企业员工每年的净增量不能超过23人.
……………………………………………………………………………………1分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com