
21.(本题满分12分)在上海世界博览会开展期间,计划选派部分高二学生参加宣传活动,报名参加的学生需进行测试,共设4道选择题,规定必须答完所有题,且答对一题得1分,答错一题扣1分,至少得2分才能入选成为宣传员;甲乙丙三名同学报名参加测试,他们答对每个题的概率都为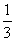 ,且每个人答题相互不受影响.
,且每个人答题相互不受影响.
(1)用随机变量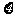 表示能够成为宣传员的人数,求
表示能够成为宣传员的人数,求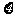 的数学期望与方差;
的数学期望与方差;
(2)若学生甲得分的数值为随机变量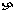 ,求所得分数
,求所得分数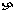 的分布列和数学期望.
的分布列和数学期望.
20. (本题满分12分)如图,在四棱锥
(本题满分12分)如图,在四棱锥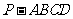 中,底面
中,底面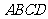 为菱形,
为菱形,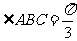 ,
,  ,
, 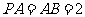 ,
,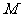 为
为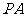 的中点,
的中点,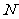 为
为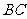 的中点
的中点
(1)证明:直线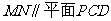
 ;
;
(2)求异面直线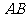 与
与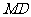 所成角的大小;
所成角的大小;
(3)求点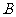 到平面
到平面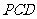 的距离.
的距离.
19.(本题满分12分)袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为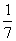 ,现有甲、乙两人从袋中轮流摸取1球.甲先取,乙后取,然后甲再取…取后不放回,每人最多取两次,若两人中有一人首先取到白球时则终止,每个球在每一次被取出的机会是等可能的.
,现有甲、乙两人从袋中轮流摸取1球.甲先取,乙后取,然后甲再取…取后不放回,每人最多取两次,若两人中有一人首先取到白球时则终止,每个球在每一次被取出的机会是等可能的.
(1)求袋中原有白球的个数;
(2)求甲取到白球的概率;
(3)求取球4次终止的概率.
18. (本题满分12分)已知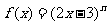 展开式的二项式系数和为512,
展开式的二项式系数和为512,
且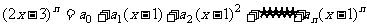
(1)求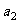 的值;
的值;
(2)求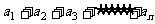 的值;
的值;
(3)求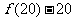 被6整除的余数.
被6整除的余数.
17.(本题满分10分)某同学练习投篮,已知他每次投篮命中率为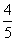 ,
,
(1)求在他第三次投篮后,首次把篮球投入篮框内的概率;
(2)若想使他投入篮球的概率达到0.99,则他至少需投多少次?(lg2=0.3)
16.三棱锥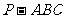 中,
中,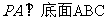 ,
,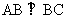 ,
,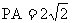 ,
,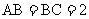 ,若
,若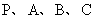 四点在同一个球面上,则在球面上
四点在同一个球面上,则在球面上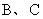 两点之间的球面距离是_____ .
两点之间的球面距离是_____ .
15.高二年级某班共有60名学生,在一次考试中,其数学成绩满足正态分布,数学平均分为100分,若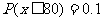 (
(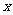 表示本班学生数学分数),求分数在
表示本班学生数学分数),求分数在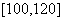 的人数____ ;
的人数____ ;
14.甲乙二人进行射击游戏,目标靶上有三个区域,分别涂有红、黄、蓝三色,已知甲击中红、黄、蓝三区域的概率依次是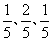 ,乙击中红、黄、蓝三区域的概率依次是
,乙击中红、黄、蓝三区域的概率依次是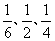 ,二人射击情况互不影响,若甲乙各射击一次,试预测二人命中同色区域的概率________
;
,二人射击情况互不影响,若甲乙各射击一次,试预测二人命中同色区域的概率________
;
13.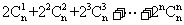 等于_____________;
等于_____________;
12. 正四棱柱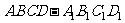 中,
中,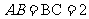 ,
,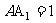 ,则异面直线
,则异面直线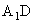 与
与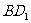 所成角的余弦值为( )
所成角的余弦值为( )
A.0
B.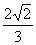 C.
C. 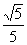 D.
D.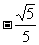
第Ⅱ卷(非选择题,共90分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com