
4、下列各句中,没有语病的一项是 ( )
A.一个人工作能力的高低,不在于他掌握了多少知识,关键看他做出突出的成绩。
B.任何一届世博会的成功,不仅记录了人类文明的一个个脚印,而且表达着人类对时代和未来的思考。
C.云南热带作物资源、矿产资源和水电资源,都使云南跻身为国内资源最丰富的省份。
D.发扬并继承中华民族的优秀文化传统,是我们每个华夏子孙义不容辞的责任。
3、在下列句子横线上依次填入词语,最恰当的一组是 ( )
一位哲人说过,自然是伟大的一部书:“ 你认识了这一部书,你在这世界上寂寞时便不寂寞,贫困时便不贫困,苦恼时有 ,挫折时有 ,软弱时有督责,迷失时有 。”
A.只有 鼓励 方向 安慰
B.只要 安慰 鼓励 方向
C.只要 方向 鼓励 安慰
D.只有 鼓励 安慰 方向
2、下列句子中,加点成语使用不正确的一项是 ( )
A.做一个人,我们要行使自己的权利;做一个公民,我们要恪尽职守。
B.梯田上面,有漫漫云海的覆盖;梯田旁边,是茫茫森林的掩映。此景真是神奇瑰丽、莫可名状,让人惊叹。
C.十四年未曾谋面的老同学在长城上萍水相逢,共叙别后之情。
D.每一个舞姿都使人颤栗在浓烈的艺术享受中,使人叹为观止。
1. 下列各项中加点的字的注音和字形都正确的一项是 ( )
A. 蝉蜕(tuì) 省(xǐng)悟 重蹈覆(fù)辙 吹毛求疵(cī)
B. 栖(qī)息 炮(pào)制 莫名奇(qí)妙 断章取(qǚ)义
C. 胆怯(què) 匀称(chèn) 颔(hàn)首低首 粗制烂(làn)造
D. 唱和(hè) 玷(zhān)污 相辅相成(chéng) 走头(tóu)无路
(17)(本小题满分12分)
在 中,
中, 分别为内角
分别为内角 的对边,
的对边,
且
(Ⅰ)求 的大小;
的大小;
(Ⅱ)若 ,试判断
,试判断 的形状.
的形状.
解:(Ⅰ)由已知,根据正弦定理得
即
由余弦定理得
故
(Ⅱ)由(Ⅰ)得
又 ,得
,得
因为 ,
,
故
所以 是等腰的钝角三角形。
是等腰的钝角三角形。
(18)(本小题满分12分)
为了比较注射A,B两种药物后产生的皮肤疱疹的面积,选200只家兔做实验,将这200只家兔随机地分成两组。每组100只,其中一组注射药物A,另一组注射药物B。下表1和表2分别是注射药物A和药物B后的实验结果。(疱疹面积单位: )
)
(Ⅰ)完成下面频率分布直方图,并比较注射两种药物后疱疹面积的中位数大小;
(Ⅱ)完成下面 列联表,并回答能否有99.9%的把握认为“注射药物A后的疱疹面积与注射药物B后的疱疹面积有差异”。 K^S*5U.C#
列联表,并回答能否有99.9%的把握认为“注射药物A后的疱疹面积与注射药物B后的疱疹面积有差异”。 K^S*5U.C#

附:
解:
(Ⅰ)
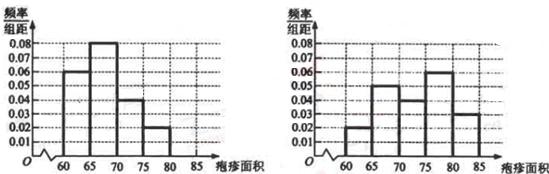
图1注射药物A后皮肤疱疹面积的频率分布直方图 图2注射药物B后皮肤疱疹面积的频率分布直方图
可以看出注射药物A后的疱疹面积的中位数在65至70之间,而注射药物B后的疱疹面积的中位数在70至75之间,所以注射药物A后疱疹面积的中位数小于注射药物B后疱疹面积的中位数。
(Ⅱ)表3
|
|
疱疹面积小于 |
疱疹面积不小于 |
合计 |
注射药物 |
 |
 |
 |
注射药物 |
 |
 |
 |
|
合计 |
 |
 |
 |

由于 ,所以有99.9%的把握认为“注射药物A后的疱疹面积与注射药物B后的疱疹面积有差异”.
,所以有99.9%的把握认为“注射药物A后的疱疹面积与注射药物B后的疱疹面积有差异”.
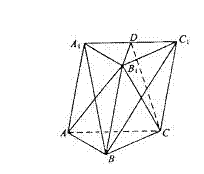
(19)(本小题满分12分)
如图,棱柱 的侧面
的侧面 是菱形,
是菱形,
(Ⅰ)证明:平面
 平面
平面 ;
;
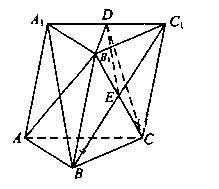 (Ⅱ)设
(Ⅱ)设 是
是 上的点,且
上的点,且 平面
平面 ,求
,求 的值.
的值.
解:(Ⅰ)因为侧面BCC1B1是菱形,所以
又已知
所又 平面A1BC1,又
平面A1BC1,又 平面AB1C ,
平面AB1C ,
所以平面 平面A1BC1 .
平面A1BC1 .
(Ⅱ)设BC1交B1C于点E,连结DE,
则DE是平面A1BC1与平面B1CD的交线,
因为A1B//平面B1CD,所以A1B//DE.
又E是BC1的中点,所以D为A1C1的中点.
即A1D:DC1=1.
(20)(本小题满分12分) K^S*5U.C#
设 ,
, 分别为椭圆
分别为椭圆
 的左、右焦点,过
的左、右焦点,过 的直线
的直线 与椭圆
与椭圆 相交于
相交于 ,
, 两点,直线
两点,直线 的倾斜角为
的倾斜角为 ,
, 到直线
到直线 的距离为
的距离为 .
.
(Ⅰ)求椭圆 的焦距;
的焦距;
(Ⅱ)如果 ,求椭圆
,求椭圆 的方程.
的方程.
解:(Ⅰ)设焦距为 ,由已知可得
,由已知可得 到直线l的距离
到直线l的距离
所以椭圆 的焦距为4.
的焦距为4.
(Ⅱ)设 直线
直线 的方程为
的方程为
联立
解得
因为
即
得
故椭圆 的方程为
的方程为
(21)(本小题满分12分)
已知函数 .
.
(Ⅰ)讨论函数 的单调性; K^S*5U.C#
的单调性; K^S*5U.C#
(Ⅱ)设 ,证明:对任意
,证明:对任意 ,
, .
.
解:(Ⅰ) f(x)的定义域为(0,+ ),
), .
.
当a≥0时, >0,故f(x)在(0,+
>0,故f(x)在(0,+ )单调增加;
)单调增加;
当a≤-1时, <0, 故f(x)在(0,+
<0, 故f(x)在(0,+ )单调减少;
)单调减少;
当-1<a<0时,令 =0,解得x=
=0,解得x= .当x∈(0,
.当x∈(0,  )时,
)时,  >0;
>0;
x∈( ,+
,+ )时,
)时, <0, 故f(x)在(0,
<0, 故f(x)在(0,  )单调增加,在(
)单调增加,在( ,+
,+ )单调减少.
)单调减少.
(Ⅱ)不妨假设x1≥x2.由于a≤-2,故f(x)在(0,+ )单调减少.
)单调减少.
所以 等价于
等价于
 ≥4x1-4x2,
≥4x1-4x2,
即f(x2)+ 4x2≥f(x1)+ 4x1.
令g(x)=f(x)+4x,则
 +4
+4
= .
.
于是 ≤
≤ =
= ≤0.
≤0.
从而g(x)在(0,+ )单调减少,故g(x1) ≤g(x2),
)单调减少,故g(x1) ≤g(x2),
即 f(x1)+ 4x1≤f(x2)+
4x2,故对任意x1,x2∈(0,+ ) ,
) , .
.
请考生在第(22)、(23)、(24)三题中任选一题做答,如果多做,则按所做的第一题记分。做答时用2B铅笔在答题卡上把所选题目对应题号下方的方框涂黑。
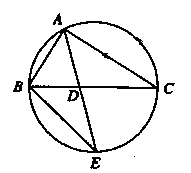 (22)(本小题满分10分)选修4-1:几何证明选讲
(22)(本小题满分10分)选修4-1:几何证明选讲
如图, 的角平分线
的角平分线 的延长线交它的外接圆于点
的延长线交它的外接圆于点
(Ⅰ)证明: ∽△
∽△ ;
;
(Ⅱ)若 的面积
的面积 ,求
,求 的大小.
的大小.
证明:(Ⅰ)由已知条件,可得∠BAE=∠CAD.
因为∠AEB与∠ACB是同弧上的圆周角,所以∠AEB=∠ACD.
故△ABE∽△ADC.
(Ⅱ)因为△ABE∽△ADC,所以 ,即AB·AC=AD·AE.
,即AB·AC=AD·AE.
又S= AB·ACsin∠BAC,且S=
AB·ACsin∠BAC,且S= AD·AE,故AB·ACsin∠BAC=AD·AE.
AD·AE,故AB·ACsin∠BAC=AD·AE.
则sin∠BAC=1,又∠BAC为三角形内角,所以∠BAC=90°.
(23)(本小题满分10分)选修4-4:坐标系与参数方程
已知P为半圆C: (
( 为参数,0≤
为参数,0≤ ≤
≤ )上的点,点A的坐标为(1,0),O为坐标原点,点M在射线OP上,线段OM与C的弧
)上的点,点A的坐标为(1,0),O为坐标原点,点M在射线OP上,线段OM与C的弧 的长度均为
的长度均为 .
.
(Ⅰ)以O为极点,x轴的正半轴为极轴建立极坐标系,求点M的极坐标;
(Ⅱ)求直线AM的参数方程.
解:(Ⅰ)由已知,M点的极角为 ,且M点的极径等于
,且M点的极径等于 ,
,
故点M的极坐标为( ,
, )
)
(Ⅱ)M点的直角坐标为( ),A(l,0),故直线AM的参数方程为
),A(l,0),故直线AM的参数方程为
 (t为参数).
(t为参数).
(24)(本小题满分10分)选修4-5:不等式选讲
已知a,b,c均为正数,证明:a2+b2+c2+ ≥6
≥6 ,并确定a,b,c为何值时,
,并确定a,b,c为何值时,
等号成立.
证明:(证法一)
因为a,b,c均为正数,由平均值不等式得
a2+b2+c2≥ ①
①
 ≥
≥
所以 ≥
≥ . ②
. ②
故a2+b2+c2+ ≥
≥

又
 ≥
≥ , ③
, ③
所以原不等式成立.
当且仅当a=b=c时,①式和②式等号成立.当且仅当 时, ③式等号成立.
时, ③式等号成立.
即当且仅当a=b=c= 时,原式等号成立.
时,原式等号成立.
(证法二)
因为a,b,c均为正数,由基本不等式
a2+b2≥2ab,
b2+c2≥2bc
c2+a2≥2ac.
所以a2+b2+c2≥ab+bc+ac ①
同理 ≥
≥ ②
②
故a2+b2+c2+( )2
)2
≥ab+bc+ac+3 +3
+3 +3
+3
≥6 . ③
. ③
所以原不等式成立
当且仅当a=b=c时,①式和②式等号成立,当且仅当a=b=c,(ab)2=(bc)2=(ac)2=3时,③式等号成立.
即当且仅当a=b=c= 时,原式等号成立.
时,原式等号成立.
版权所有:()
版权所有:()
(13)三张卡片上分别写上字母E、E、B,将三张卡片随机地排成一行,恰好排成英文单词BEE的概率为 。
解析:填 题中三张卡片随机地排成一行,共有三种情况:
题中三张卡片随机地排成一行,共有三种情况: ,
, 概率为:
概率为: K^S*5U.C#
K^S*5U.C#
(14)设 为等差数列
为等差数列 的前
的前 项和,若
项和,若 ,则
,则 。
。
解析:填15.  ,解得
,解得 ,
, K^S*5U.C#
K^S*5U.C#
(15)已知 且
且 ,则
,则 的取值范围是
.
的取值范围是
.
(答案用区间表示)
 解析:填
解析:填 . 利用线性规划,画出不等式组
. 利用线性规划,画出不等式组 表示的平面区域,即可求解.K^S*5U.C#
表示的平面区域,即可求解.K^S*5U.C#
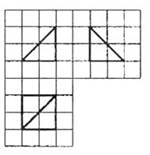
(16)如图,网格纸的小正方形的边长是1,在其上用粗线画
出了某多面体的三视图,则这个多面体最长的一条棱的
长为 .
 解析:填
解析:填 画出直观图:图中四棱锥
画出直观图:图中四棱锥 即是,
即是,
所以最长的一条棱的长为
(1)已知集合 ,
, ,则
,则
(A) (B)
(B) (C)
(C) (D)
(D)
解析:选D. 在集合 中,去掉
中,去掉 ,剩下的元素构成
,剩下的元素构成
(2)设 为实数,若复数
为实数,若复数 ,则
,则
(A) (B)
(B) (C)
(C) (D)
(D)
解析:选A.  ,因此
,因此 .
.
(3)设 为等比数列
为等比数列 的前
的前 项和,已知
项和,已知 ,
, ,则公比
,则公比
(A)3 (B)4 (C)5 (D)6
解析:选B. 两式相减得,  ,
, .
.
 (4)已知
(4)已知 ,函数
,函数 ,若
,若 满足关于
满足关于 的方程
的方程 ,则下列选项的命题中为假命题的是
,则下列选项的命题中为假命题的是
(A) (B)
(B)
(C)  (D)
(D)
解析:选C.函数 的最小值是
的最小值是
等价于 ,所以命题
,所以命题 错误.
错误.
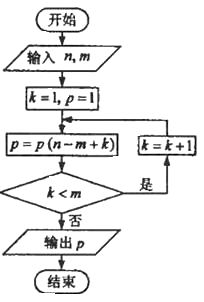
(5)如果执行右面的程序框图,输入 ,那么输出的
,那么输出的 等于
等于
(A)720 (B) 360 (C) 240 (D) 120
解析:选B.
(6)设 ,函数
,函数 的图像向右平移
的图像向右平移 个单位后与原图像重合,则
个单位后与原图像重合,则 的最小值是
的最小值是
(A) (B)
(B)  (C)
(C)  (D) 3
(D) 3
解析:选C.由已知,周期
(7)设抛物线 的焦点为
的焦点为 ,准线为
,准线为 ,
, 为抛物线上一点,
为抛物线上一点, ,
, 为垂足,如果直线
为垂足,如果直线 斜率为
斜率为 ,那么
,那么
(A) (B) 8 (C)
(B) 8 (C)  (D) 16
(D) 16
解析:选B.利用抛物线定义,易证 为正三角形,则
为正三角形,则
(8)平面上 三点不共线,设
三点不共线,设 ,则
,则 的面积等于 K^S*5U.C#
的面积等于 K^S*5U.C#
(A) (B)
(B)
(C) (D)
(D)
解析:选C.


(9)设双曲线的一个焦点为 ,虚轴的一个端点为
,虚轴的一个端点为 ,如果直线
,如果直线 与该双曲线的一条渐近线垂直,那么此双曲线的离心率为
与该双曲线的一条渐近线垂直,那么此双曲线的离心率为
(A) (B)
(B) (C)
(C) (D)
(D)
解析:选D.不妨设双曲线的焦点在 轴上,设其方程为:
轴上,设其方程为: ,
,
则一个焦点为
一条渐近线斜率为: ,直线
,直线 的斜率为:
的斜率为: ,
, ,
,
 ,解得
,解得 .
.
(10)设 ,且
,且 ,则
,则
(A) (B)10 (C)20 (D)100
(B)10 (C)20 (D)100
解析:选A. 又
又
(11)已知 是球
是球 表面上的点,
表面上的点, ,
, ,
, ,
, ,则球
,则球 的表面积等于
的表面积等于
(A)4 (B)3
(B)3 (C)2
(C)2 (D)
(D)
解析:选A.由已知,球 的直径为
的直径为 ,
, 表面积为
表面积为
(12)已知点 在曲线
在曲线 上,
上, 为曲线在点
为曲线在点 处的切线的倾斜角,则
处的切线的倾斜角,则 的取值范围是
的取值范围是
(A)[0, ) (B)
) (B) (C)
(C)  (D)
(D) 
解析:选D. ,
, ,
,
即 ,
,
第Ⅱ卷
本试卷包括必考题和选考题两部分。第(13)题-第(21)题为必考题,每个试题考生都必须作答。第(22)题-第(24)题为选考题,考生根据要求作答。
16.(16分)(1)(5分)E 、G 、R,基 。
(2)(4分) 及 。
(3)(3分)X 、Y 、Z 。
(4)(4分)①
② 。
15.(13分)(1)(3分)____________,
(2)(4分) ;: ;
(3)(2分) mol。
(4)(4分) ;
。
14.(14分)
Ⅰ.(10分) (1)(2分)_____________________________________
(2)(6分)鉴别甲的方法:_____________________________________________
鉴别乙的方法:_____________________________________________
鉴别丙的方法:_____________________________________________
(3)(2分)_______________
II(4分) ,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com