第二节　 听取信息(共5小题；每小题1分，满分5分)

听下面一段独白，请根据题目要求，从所听到的内容中获取必要的信息，填入答题卡标号为16-20的空格中。听录音前，你将有10秒钟的阅题时间。录音读两遍，你将有60秒钟的作答时间。

21．(本小题满分14分)

设是数列的前项和，且是和的等差中项．

(1)求数列的通项公式；

(2)当(均为正整数)时，求和的所有可能的乘积之和；

(3)设，求证：．

2010年深圳市高三年级第二次调研考试

20．(本小题满分14分)

已知抛物线：的焦点为，过点作直线交抛物线于、两点；椭圆的中心在原点，焦点在轴上，点是它的一个顶点，且其离心率．

(1)求椭圆的方程；

(2)经过、两点分别作抛物线的切线、，切线与相交于点．证明：；

(3) 椭圆上是否存在一点，经过点作抛物线的两条切线、(、为切点)，使得直线过点？若存在，求出抛物线与切线、所围成图形的面积；若不存在，试说明理由．

19．(本小题满分14分)

设函数(，)．

(1)若函数在其定义域内是减函数，求的取值范围；

(2)函数是否有最小值？若有最小值，指出其取得最小值时的值，并证明你的结论．

18．(本小题满分14分)

如图5，四边形是圆柱的轴截面，点在圆柱的底面圆周上，是的中点，圆柱的底面圆的半径，侧面积为，．

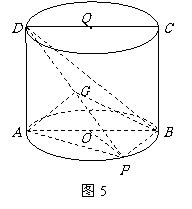(1)求证：；

(2)求二面角的平面角的余弦值．

17．(本小题满分12分)

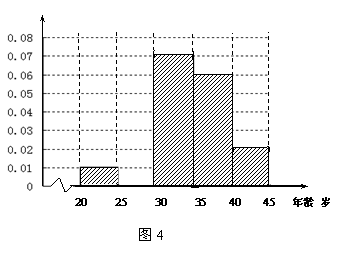
上海世博会深圳馆1号作品《大芬丽莎》是由大芬村507名画师集体创作的999幅油画组合而成的世界名画《蒙娜丽莎》，因其诞生于大芬村，因此被命名为《大芬丽莎》．某部门从参加创作的507名画师中随机抽出100名画师，测得画师年龄情况如下表所示．

(1)频率分布表中的①、②位置应填什么数据？并在答题卡中补全频率分布直方图(图4)，再根据频率分布直方图估计这507个画师中年龄在岁的人数(结果取整数)；

(2)在抽出的100名画师中按年龄再采用分层抽样法抽取20人参加上海世博会深圳馆志愿者活动，其中选取2名画师担任解说员工作，记这2名画师中“年龄低于30岁”的人数为ξ，求ξ的分布列及数学期望．

分组 (单位：岁)	频数	频率
	5	0.050
	①	0.200
	35	②
	30	0.300
	10	0.100
合计	100	1.00

16．(本小题满分12分)

已知，，设．

(1)求函数的最小正周期及其单调递增区间；

(2)若分别是锐角的内角的对边，且，，试求的面积．

(二)选做题(14、15题，考生只能从中选做一题)

14．(坐标系与参数方程选做题)

在极坐标系中，若圆的极坐标方程为，若以极点为原点，以极轴为轴的正半轴建立相应的平面直角坐标系中，则在直角坐标系中，圆心的直角坐标是　　　　 ．

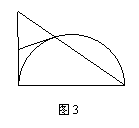
15．(几何证明选讲选做题)

如图3，在中，，以为直径作半圆交于，过作半圆的切线交于，若，，则=　　 　　　．