
补充:1.利用余弦线比较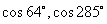 的大小;
的大小;
2.若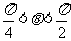 ,则比较
,则比较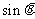 、
、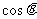 、
、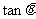 的大小;
的大小;
3.利用单位圆比较三角函数值的大小,求角的范围。
2.会画任意角的三角函数线;
1.三角函数线的定义;
4.例题分析:
例1.作出下列各角的正弦线、余弦线、正切线。
(1)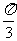 ; (2)
; (2)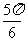 ; (3)
; (3)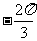 ; (4)
; (4)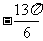 .
.
解:图略。
例2.利用三角函数线比较下列各组数的大小:
1° 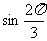 与
与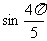 2° tan
2° tan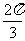 与tan
与tan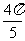 3° cot
3° cot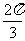 与cot
与cot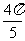
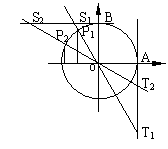 解: 如图可知:
解: 如图可知:
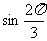
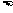
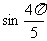
tan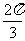
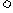 tan
tan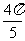
cot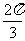
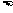 cot
cot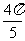
例3.利用单位圆寻找适合下列条件的0°到360°的角
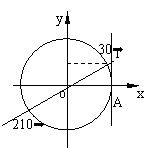
 1° sina≥
1° sina≥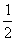 2° tana
2° tana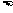
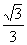
解: 1° 2°
30°≤a≤150° 30°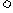 a
a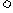 90°或210°
90°或210°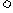 a
a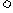 270°
270°
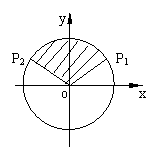
例4.利用单位圆写出符合下列条件的角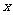 的范围。
的范围。
(1)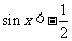 ;
(2)
;
(2)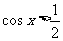 ;
;
(3)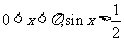 且
且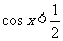 ;
;
(4)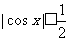 ;
(5)
;
(5)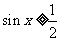 且
且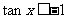 .
.
答案:(1)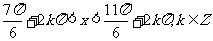 ;(2)
;(2)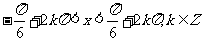 ;
;
(3)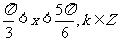 ;(4)
;(4)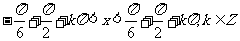 ;
;
(5)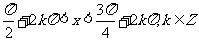 .
.
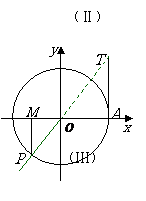
3.三角函数线的定义:
设任意角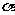 的顶点在原点
的顶点在原点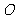 ,始边与
,始边与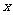 轴非负半轴重合,终边与单位圆相交与点
轴非负半轴重合,终边与单位圆相交与点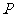
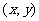 ,
,
过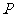 作
作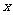 轴的垂线,垂足为
轴的垂线,垂足为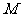 ;过点
;过点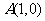 作单位圆的切线,它与角
作单位圆的切线,它与角 的终边或其反向延
的终边或其反向延
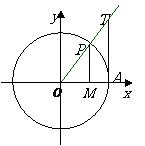
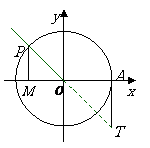 长线交与点
长线交与点 .
.
 |
|||||
|
|||||
 |
|||||
由四个图看出:
当角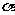 的终边不在坐标轴上时,有向线段
的终边不在坐标轴上时,有向线段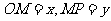 ,于是有
,于是有
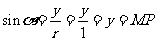 ,
, 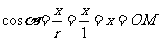 ,
,
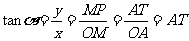 .
.
我们就分别称有向线段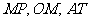 为正弦线、余弦线、正切线。
为正弦线、余弦线、正切线。
说明:
①三条有向线段的位置:正弦线为 的终边与单位圆的交点到
的终边与单位圆的交点到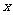 轴的垂直线段;余弦
轴的垂直线段;余弦
线在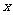 轴上;正切线在过单位圆与
轴上;正切线在过单位圆与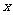 轴正方向的交点的切线上,三条有向线段中两条在单位
轴正方向的交点的切线上,三条有向线段中两条在单位
圆内,一条在单位圆外。
②三条有向线段的方向:正弦线由垂足指向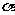 的终边与单位圆的交点;余弦线由原点指向垂
的终边与单位圆的交点;余弦线由原点指向垂
足;正切线由切点指向与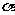 的终边的交点。
的终边的交点。
③三条有向线段的正负:三条有向线段凡与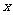 轴或
轴或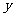 轴同向的为正值,与
轴同向的为正值,与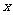 轴或
轴或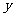 轴反向的
轴反向的
为负值。
④三条有向线段的书写:有向线段的起点字母在前,终点字母在后面。
2.有向线段:
坐标轴是规定了方向的直线,那么与之平行的线段亦可规定方向。
规定:与坐标轴方向一致时为正,与坐标方向相反时为负。
当角的终边上一点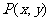 的坐标满足
的坐标满足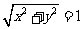 时,有三角函数正弦、余弦、正切值的几何表示--三角函数线。
时,有三角函数正弦、余弦、正切值的几何表示--三角函数线。
1.单位圆:圆心在圆点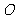 ,半径等于单位长的圆叫做单位圆。
,半径等于单位长的圆叫做单位圆。
3.诱导公式:
练习3:求下列三角函数的值:
(1)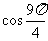 , (2)
, (2)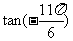 , (3)
, (3)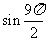 .
.
2.三角函数的符号:
练习2:已知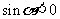 且
且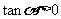 ,
,
(1)求角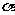 的集合;(2)求角
的集合;(2)求角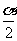 终边所在的象限;(3)试判断
终边所在的象限;(3)试判断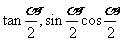 的符号。
的符号。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com