
34.(江西卷)
已知向量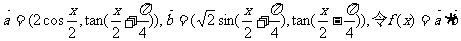 .
.
求函数f(x)的最大值,最小正周期,并写出f(x)在[0,π]上的单调区间.
.解: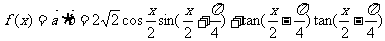
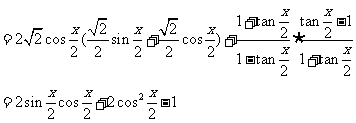
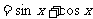
=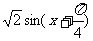 .
.
所以 ,最小正周期为
,最小正周期为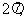
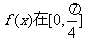 上单调增加,
上单调增加,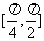 上单调减少.
上单调减少.
33.(浙江卷)已知函数f(x)=2sinxcosx+cos2x.
(Ⅰ) 求f(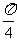 )的值;(Ⅱ) 设
)的值;(Ⅱ) 设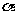 ∈(0,
∈(0,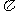 ),f(
),f(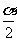 )=
)=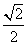 ,求sin
,求sin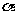 的值.
的值.
解:(Ⅰ)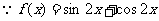
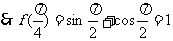
(Ⅱ) 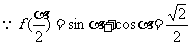
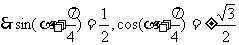
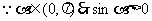
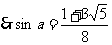
32.(浙江卷)已知函数f(x)=-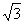 sin2x+sinxcosx.
sin2x+sinxcosx.
(Ⅰ) 求f(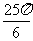 )的值; (Ⅱ) 设
)的值; (Ⅱ) 设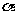 ∈(0,
∈(0,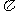 ),f(
),f(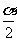 )=
)=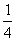 -
-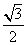 ,求sin
,求sin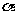 的值.
的值.
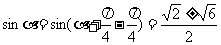
解:(Ⅰ) 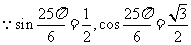
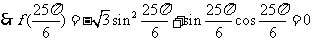
(Ⅱ) 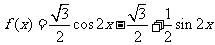
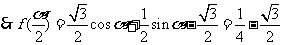
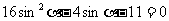 解得
解得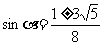
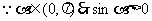
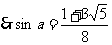
28.(广东卷)
化简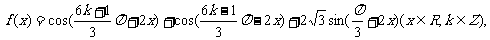 并求函数
并求函数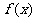 的值域和最小正周期.
的值域和最小正周期.
.解:
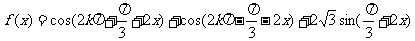
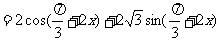
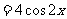
所以函数f(x)的值域为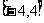 ,最小正周期
,最小正周期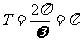
29(北京卷) 已知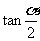 =2,求
=2,求
(I)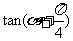 的值; (II)
的值; (II)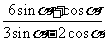 的值.
的值.
解:(I)∵
tan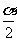 =2, ∴
=2, ∴ 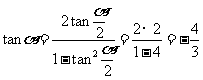 ;
;
所以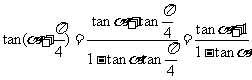 =
=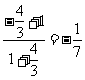 ;
;
(II)由(I), tanα=-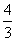 , 所以
, 所以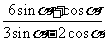 =
=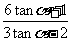 =
=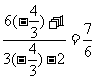 .
.
30(全国卷Ⅰ)
设函数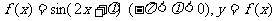 图像的一条对称轴是直线
图像的一条对称轴是直线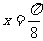 。
。
(Ⅰ)求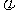 ;(Ⅱ)求函数
;(Ⅱ)求函数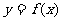 的单调增区间;
的单调增区间;
(Ⅲ)画出函数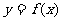 在区间
在区间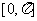 上的图像。
上的图像。
.本小题主要考查三角函数性质及图像的基本知识,考查推理和运算能力,满分12分.
解:(Ⅰ) 的图像的对称轴,
的图像的对称轴,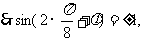
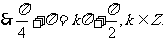
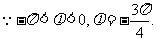
(Ⅱ)由(Ⅰ)知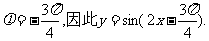
由题意得 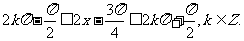
所以函数
(Ⅲ)由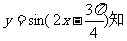
|
x |
0 |
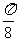 |
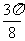 |
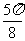 |
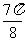 |
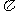 |
|
y |
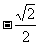 |
-1 |
0 |
1 |
0 |
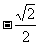 |
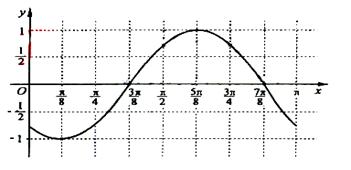 故函数
故函数
31(全国卷Ⅱ)已知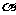 为第二象限的角,
为第二象限的角,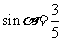 ,
,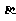 为第一象限的角,
为第一象限的角,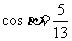 .求
.求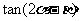 的值.
的值.
27.(重庆卷)已知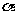 、
、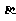 均为锐角,且
均为锐角,且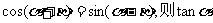 =
1 .
=
1 .
解答题:
26.(湖南卷)设函数f
(x)的图象与直线x =a,x =b及x轴所围成图形的面积称为函数f(x)在[a,b]上的面积,已知函数y=sinnx在[0,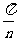 ]上的面积为
]上的面积为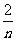 (n∈N*
),(i)y=sin3x在[0,
(n∈N*
),(i)y=sin3x在[0,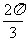 ]上的面积为
]上的面积为 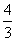 ;(ii)y=sin(3x-π)+1在[
;(ii)y=sin(3x-π)+1在[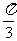 ,
,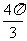 ]上的面积为
]上的面积为 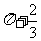 .
.
25.(湖北卷)函数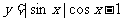 的最小正周期与最大值的和为
的最小正周期与最大值的和为 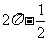 .
.
24.(上海卷)若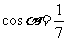 ,
,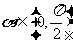 ,则
,则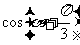 =__________。
=__________。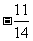
23.(上海卷)函数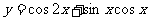 的最小正周期T=__________。
的最小正周期T=__________。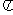
22.(上海卷)函数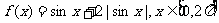 的图象与直线
的图象与直线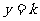 有且仅有两个不同的交点,则
有且仅有两个不同的交点,则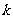 的取值范围是__________。
的取值范围是__________。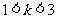
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com