4、逻辑事理

　从逻辑事理入手。中学课文虽没有章节专门介绍逻辑知识，但在修改病句时却常需要一定的逻辑知识。平时应注意掌握一些基本的逻辑知识。有些句子在逻辑上出现毛病，修改时就要从逻辑角度加以考虑。

　汽车在蜿蜒的山道上急驰，如离弦之箭一般。

　“离弦之箭”是笔直向前的，而“蜿蜒”是曲曲折折的，句子中的比喻不合事理，不合逻辑。应改为“汽车在高速公路上急驰，如离弦之箭一般。”

　综上所述，修改病句可以概括为五字诀：

　增(成分残缺的)

　删(多余的)

　换(用词不妥当的)

　简(修改应简要)

　调(不搭配、不照应的)

　修改不是再造，切忌改变句子的本意。尤其应注意，能调整语序就不增删，能改一处解决了的，决不改动两处，改病句也应简要、高效。

　总之，高考试卷中的病句辨析题有一定的难度，“病因”不是很容易看得出来。我们做此类题，除了熟练运用相关的语法知识、逻辑知识外，一定要“惕然为戒，视为止，行为迟”，仔细地琢磨句子，细察猜析，切莫轻易相信平时的“语感”，要克服粗枝大叶套用程式的弊端。

知能演练

[能力提升]

3、词法角度

　从词法角度入手，看看句子的修饰语同中心语的搭配是否恰当，句子的实词、虚词的运用是否恰当。

　语文课下课后，黄晓静交给老师二篇课外完成的作文。

　这个句子中数词运用不当，应把“二”改成“两”。如不说“二张桌子”“二盏灯”，而说“两张桌子”“两盏灯”。

2、语法角度

　从语法角度入手，抓住句子主干。无论是单句、复句，抓住了句子主干，也就抓住了句子的基本意思，在改病句时有利于保留原意。抓住主干时要注意辨认主干是否有毛病，如是否有成分残缺，主谓、动宾搭配不当等毛病，要先予以改正。

　粮库主任的失职，使40吨小麦霉烂变质。 上级领导为了严肃法纪，决定给他行政记过处分，并赔偿部分经济损失。

　这个句子的主干是“上级领导……决定……并赔偿……”显然有悖整个句子的意思，“赔偿”的人应该是失职的粮库主任，而不是上级领导。应在“赔偿”前面加上“责令他”。

4、逻辑意义分析法

　有的语病从语法上不好找毛病，就得从事理上进行分析，这就是逻辑意义分析法。逻辑意义分析法要从概念使用、判断、推理方面考虑是否得当，语句的前后顺序、句间关系是否合适。例如：

　①该市有人不择手段仿照伪劣产品……

　②凡是有杰出成就的人，都是在艰苦环境中磨炼成才的。

　①句“仿造伪劣产品”是不合事理的，应改为“制造伪劣产品”或“仿造名牌产品”。②句用了“凡是……都”这个全称肯定判断，言过其实了，应将“凡是”改为“大多”，后边删去“都”字。

　概括起来病句辨析的基本步骤是：一语感，二语法，三修辞，四逻辑。

　了解病句的几种常见类型，特别是《考试说明》中指出的6种类型，把握了一定的辨析病句的方法，还要熟悉改病句的常规方法。修改病句的目的是为了使句子表达准确，语句明白无误。此时应该遵循几条原则。

　l、保留原意

　修改病句时，必须保留原意，不可改走样。

　一走进西湖公园，就看到公园里彩旗飘扬，歌声嘹亮。

　这个句子犯的是搭配不当的毛病，“彩旗飘扬”可以看到，“歌声隙亮”却看不到。修改这个病句时，不能因为搭配不当就把“歌声嘹亮”删去，因为整个句子是要从两个方面来表现公园的热闹非凡的，删去“歌声嘹亮”就把句子的原意给改了。这个句子可以改成“一走进西湖公园，就看到彩旗飘扬，听到歌声嘹亮”。

3、造句类比法

　有的句子是否有毛病，一时拿不准，这时仿照原句的结构造日常用的句子，经过比较问题就清楚了。例如：

　这个经验值得文教工作者特别是中小学教师的重视。

　原句结构复杂，先压缩化简为“这值得他们的重视”。再比照它的结构造句：“这值得他们的学习”。“这值得我们的参观。”这三个句子和日常说法相比多了一个“的”字，原句要将“教师的重视”中的“的”删去。

2、主干枝叶梳理法

　运用语法分析的手段，先将句子中的附加成分(定语、状语、补语)去掉，紧缩出主干，检查主干是否有毛病；如果主干没问题，再检查局部，看修饰语和中心词之间、修饰语内部是否有毛病。例如：

　过去几万名地质队员经过数十年才能做到的事情，资源卫星几天内即可完成。

　用紧缩法，这个句子的主干是“事情卫星完成”，“事情”不能说“完成”，只能说“做完”，这儿犯了搭配不当的错误。

24、(本题满分10分)选修4-5：不等式选讲

设函数。

(I)当a=－5时，求函数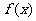的定义域。

(II)若函数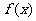的定义域为R，求实数a的取值范围。

2010-2011学年度第一学期高中教学质量监测(一)

23、(本题满分10分)选修4-4：坐标系与参数方程

设直角坐标系的原点与极坐标系的极点重合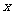，轴正半轴与极轴重合。

已知圆C的极坐标方程：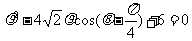

(I)将极坐标方程化为普通方程。

(II)若点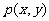在圆C上，求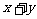的取值范围。

22、(本题满分10分) 选修4-1：几何证明选讲

如图，BA是⊙O的直径，AD是⊙O切线，C、E分别

为半圆上不同的两点，BC交AD于D，BE交AD于F。

(I) 求证：BE·BF=BC·BD。

(II) 若⊙O的半径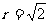，BC=1，求AD。

21、(12分)设函数，。

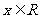(1)求函数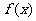的单调区间和极值。

(2)若关于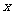的方程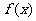=a 有三个不同实根，求实数a的取值范围。

(3)已知当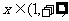时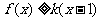，恒成立，求实数的取值范围。