2．

1．三角函数线[见课本第一册下P14]

5、无论是化简还是求证，务必非常注意角度的特点。

4、条件等式的证明要注意条件与结论之间的区别与联系，选用适当方法。

3、证明等式方法：化繁为简；左右归一；变更命题。

2、化简方法：用公式；化同角；化同名；化切割为弦；

1、化简的三种基本类型：根式形式；分式形；多项形式

例1：(1)已知为第四象限角，化简：

(2)已知，化简

解：(1)因为为第四象限角

　　　　 所以原式=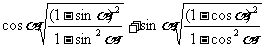

(2)，

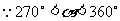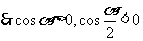
所以原式=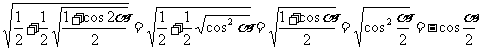

思路点拨：根式形式的三角函数式化简常采用有理化如(1)或升幂公式如(2)

例2、P(55　 例1) 　试求函数Y=sinx+cosx+2sinx cosx +2 的最大值,最小值.

若呢?

解：　　　　　　　　　　　　

练习：a,b为何值时，函数的值为2？(a=3,b=1)

思路点拨：注意角度与关系，先化简整理。

例3　　　　　　 (P57例1)

_

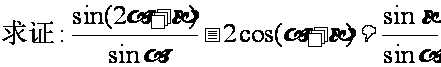
练习、求证：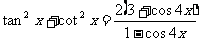

思路点拨：要据角度x与4x的特点和函数名的特点，可采用化切为弦，并用倍角公式证明。

证：左边=

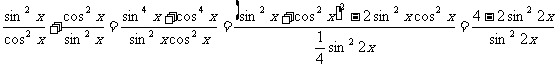
右边=

所以左边=右边，即等式成立。

本题采用了左、右归法，从左到右或从右到左见书本。

例5、综合　 P57例2

P是以F₁, F₂ 为焦点的椭圆上一点,且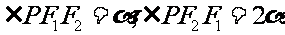

求证:椭圆的离心率e=2cosa-1

预备：例6 在ΔABC中，设tanA+tanC=2tanB,求证cos(B+C-A)=.

　 证明：

由条件得

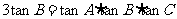
而　　　 ，

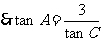
又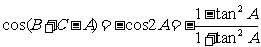

而

　cos(B+C-A)=

3、无论是化简还是证明都要注意：

(1)角度的特点

(2)函数名的特点

(3)化切为弦是常用手段

(4)升降幂公式的灵活应用

2、证明及其基本方法

(1)化繁为简法

(2)左右归一法

(3)变更命题法

(4)条件等式的证明关键在于分析已知条件与求证结论之间的区别与联系。