
7.(2009北京文)“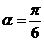 ”是“
”是“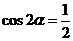 ”的
”的
A. 充分而不必要条件B.必要而不充分条件C. 充分必要条件D.既不充分也不必要条件
[答案]A
 查.当
查.当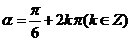 时,
时,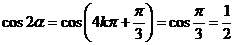 ,反之,当
,反之,当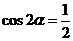 时,
时,
有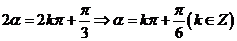 ,或
,或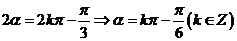 ,故应选A.
,故应选A.
6.(2009浙江文)已知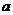 是实数,则函数
是实数,则函数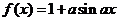 的图象不可能是( )
的图象不可能是( ) 

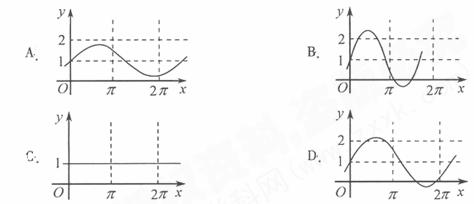
D [命题意图]此题是一个考查三角函数图象的问题,但考查的知识点因含有参数而丰富,结合图形考查使得所考查的问题形象而富有深度.
[解析]对于振幅大于1时,三角函数的周期为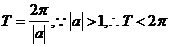 ,而D不符合要求,它的振幅大于1,但周期反而大于了
,而D不符合要求,它的振幅大于1,但周期反而大于了 .
.
5.(2009浙江理)已知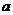 是实数,则函数
是实数,则函数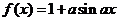 的图象不可能是
( )
的图象不可能是
( )
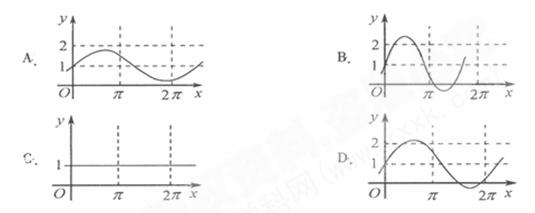
答案:D
[解析]对于振幅大于1时,三角函数的周期为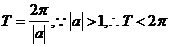 ,而D不符合要求,它的振幅大于1,但周期反而大于了
,而D不符合要求,它的振幅大于1,但周期反而大于了 .
.
4.(2009全国卷Ⅰ理)若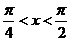 ,则函数
,则函数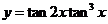 的最大值为
。
的最大值为
。
解:令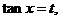
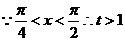 ,
, 

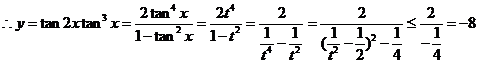


3.(2009全国卷Ⅰ理)如果函数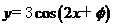 的图像关于点
的图像关于点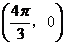 中心对称,那么
中心对称,那么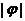 的最小值为(C)(A)
的最小值为(C)(A) (B)
(B) (C)
(C) (D)
(D) 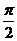


解: 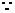 函数
函数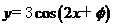 的图像关于点
的图像关于点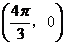 中心对称
中心对称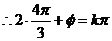
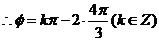 由此易得
由此易得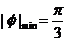 .故选C
.故选C
1.(2009年广东卷文)已知 中,
中,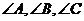 的对边分别为
的对边分别为 若
若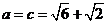 且
且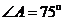 ,则
,则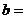
A.2 B.4+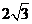 C.4-
C.4-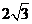 D.
D.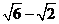

[解析]因为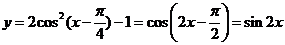 为奇函数,
为奇函数, ,所以选A.
,所以选A.
[名师点睛]掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题,能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的问题。
解三角形时,要灵活运用已知条件,根据正、余弦定理,列出方程,进而求解,最后还要检验是否符合题意。
[试题演练]
在⊿ABC中,角A、B、C所对的边分别为a、b、c,且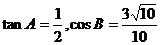

(1)求tanC的值;(2)若⊿ABC最长的边为1,求b。
解:(1)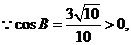
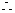 B锐角,且
B锐角,且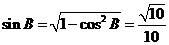 ,
,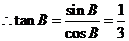 ,
, 
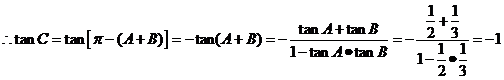

(2)由(1)知C为钝角,
C是最大角,最大边为c=1, 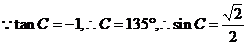 ,
, 
由正弦定理: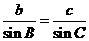 得
得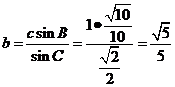 。
。

[三年高考]
07、08、09 高考试题及其解析
2009高考试题及解析
5. 一、选择题
[名师点睛]理解正、余弦函数在]0,2π],正切函数在(-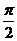 ,
,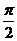 )的性质,如单调性、最大值与最小值、周期性,图象与x轴的交点,会用五点法画函数
)的性质,如单调性、最大值与最小值、周期性,图象与x轴的交点,会用五点法画函数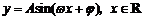 的图象,并理解它的性质:
的图象,并理解它的性质:
(1)函数图象在其对称轴处取得最大值或最小值,且相邻的最大值与最小值间的距离为其函数的半个周期;(2)函数图象与x轴的交点是其对称中心,相邻两对称中心间的距离也是其函数的半个周期;(3)函数取最值的点与相邻的与x轴的交点间的距离为其函数的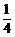 个周期。注意函数图象平移的规律,是先平移再伸缩,还是先伸缩再平移。
个周期。注意函数图象平移的规律,是先平移再伸缩,还是先伸缩再平移。
[试题演练]1已知函数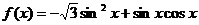

(I)求函数 的最小正周期; (II)求函数
的最小正周期; (II)求函数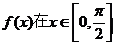 的值域.
的值域. 
解: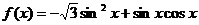
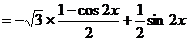

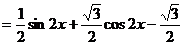
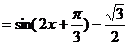 (I)
(I)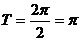

(II)∴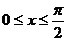 ∴
∴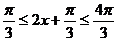 ∴
∴ 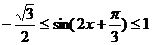

所以 的值域为:
的值域为: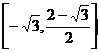

点评:本题考查三角恒等变换,三角函数图象的性质,注意掌握在给定范围内,三角函数值域的求法。
2已知函数 的最小正周期为π.(Ⅰ)求ω的值;(Ⅱ)求函数f(x)在区间[0,
的最小正周期为π.(Ⅰ)求ω的值;(Ⅱ)求函数f(x)在区间[0,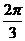 ]上的取值范围.
]上的取值范围.
解:(Ⅰ)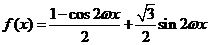 =
=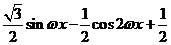

=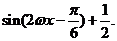 因为函数f(x)的最小正周期为π,且ω>0,所以
因为函数f(x)的最小正周期为π,且ω>0,所以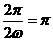 解得ω=1
解得ω=1
(Ⅱ)由(Ⅰ)得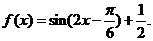 因为0≤x≤
因为0≤x≤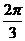 ,所以
,所以 ≤
≤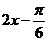 ≤
≤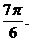

所以 ≤
≤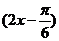 ≤1.因此0≤
≤1.因此0≤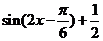 ≤
≤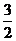 ,即f(x)的取值范围为[0,
,即f(x)的取值范围为[0,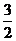 ]
]
点评:熟练掌握三角函数的降幂,由2倍角的余弦公式的三种形式可实现降幂或升幂,在训练时,要注意公式的推导过程。
3. 已知函数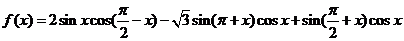 (1)求函数
(1)求函数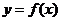 的最小正周期和最值;(2)指出
的最小正周期和最值;(2)指出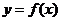 图像经过怎样的平移变换后得到的图像关于原点对称。
图像经过怎样的平移变换后得到的图像关于原点对称。
解:(1)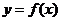 最小正周期
最小正周期 ,
,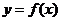 的最大值为
的最大值为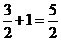 ,最小值为
,最小值为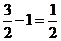

(2)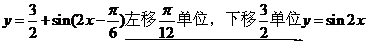

2.化简下列各式:



(1)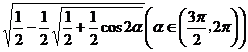 ,
, (2)
(2)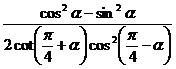 。
。



分析:(1)若注意到化简式是开平方根和2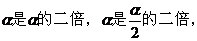 以及其范围不难找到解题的突破口;(2)由于分子是一个平方差,分母中的角
以及其范围不难找到解题的突破口;(2)由于分子是一个平方差,分母中的角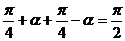 ,若注意到这两大特征,,不难得到解题的切入点.
,若注意到这两大特征,,不难得到解题的切入点.



解析:(1)因为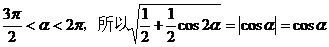 ,
,



又因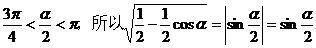 ,
,
 所以,原式=
所以,原式=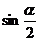 。
。



(2)原式=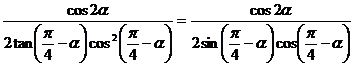



=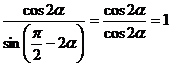 。
。



点评:如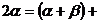
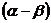 ,
,



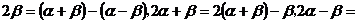
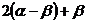 ,
,



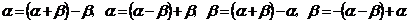 等。
等。

4.三角函数的求值类型有三类



(1)给角求值:一般所给出的角都是非特殊角,要观察所给角与特殊角间的关系,利用三角变换消去非特殊角,转化为求特殊角的三角函数值问题;



(2)给值求值:给出某些角的三角函数式的值,求另外一些角的三角函数值,解题的关键在于“变角”,如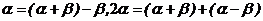 等,把所求角用含已知角的式子表示,求解时要注意角的范围的讨论;
等,把所求角用含已知角的式子表示,求解时要注意角的范围的讨论;



(3)给值求角:实质上转化为“给值求值”问题,由所得的所求角的函数值结合所求角的范围及函数的单调性求得角.



[试题演练]
1已知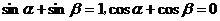 ,求cos
,求cos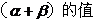 。
。



分析:因为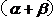 既可看成是
既可看成是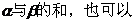 看作是
看作是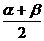 的倍角,因而可得到下面的两种解法。
的倍角,因而可得到下面的两种解法。



解法一:由已知sin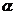 +sin
+sin =1…………①,
=1…………①,

 cos
cos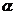 +cos
+cos =0…………②,
=0…………②,



①2+②2得 2+2cos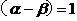 ;
;

 ∴ cos
∴ cos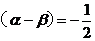 。
。



①2-②2得 cos2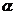 +cos2
+cos2 +2cos(
+2cos(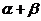 )=-1,
)=-1,



即2cos(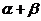 )(
)(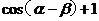 )=-1。∴
)=-1。∴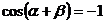 。
。



解法二:由①得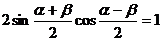 …………③
…………③



由②得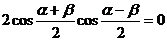 …………④
…………④



④÷③得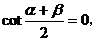



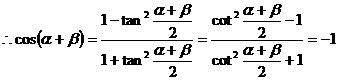




点评:此题是给出单角的三角函数方程,求复角的余弦值,易犯错误是利用方程组解sin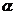 、cos
、cos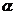 、 sin
、 sin 、 cos
、 cos ,但未知数有四个,显然前景并不乐观,其错误的原因在于没有注意到所求式与已知式的关系.本题关键在于化和为积促转化,“整体对应”巧应用。
,但未知数有四个,显然前景并不乐观,其错误的原因在于没有注意到所求式与已知式的关系.本题关键在于化和为积促转化,“整体对应”巧应用。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com