
9、(山东理5) 函数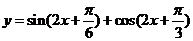 的最小正周期和最大值分别为
的最小正周期和最大值分别为
(A)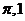 (B)
(B)
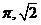 (C)
(C)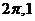 (D)
(D) 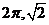
[答案]:A[分析]:化成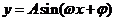 的形式进行判断即
的形式进行判断即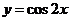 。
。
8、(广东文9)已知简谐运动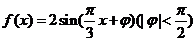 的图象经过点(0,1),则该简谐运动的最小正周期T 和初相
的图象经过点(0,1),则该简谐运动的最小正周期T 和初相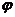 分别为
分别为
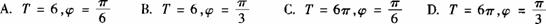
[解析]依题意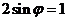 ,结合
,结合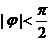 可得
可得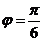 ,易得
,易得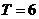 ,故选(A).
,故选(A).
7、(全国1文10)函数 的一个单调增区间是
的一个单调增区间是
A.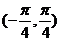 B.
B.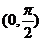 C.
C.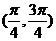 D.
D.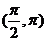
解.函数 =
=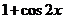 ,它的一个单调增区间是
,它的一个单调增区间是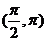 ,选D。
,选D。
6、(全国1文2)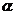 是第四象限角,
是第四象限角,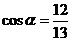 ,则
,则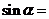
A.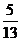 B.
B. C.
C. 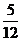 D.
D.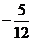
解.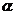 是第四象限角,
是第四象限角,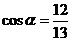 ,则
,则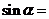
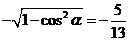 ,选B。
,选B。
5、(天津文9)设函数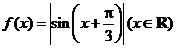 ,则
,则 ( )
( )
A.在区间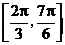 上是增函数 B.在区间
上是增函数 B.在区间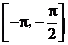 上是减函数
上是减函数
C.在区间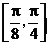 上是增函数 D.在区间
上是增函数 D.在区间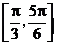 上是减函数
上是减函数
解.A [解析]由函数图象的变换可知: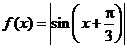 的图象是将
的图象是将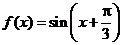 的图象
的图象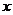 轴下方的对折上去,此时函数的最小正周期变为
轴下方的对折上去,此时函数的最小正周期变为 ,则函数在区间
,则函数在区间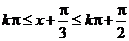 即
即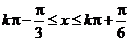 上为增函数,当
上为增函数,当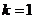 时有:
时有:
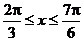 ,故在区间
,故在区间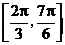 上
上 是增函数.
是增函数.
4、(天津理3) 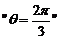 是
是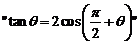 的 ( )
的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
[答案]A
[分析]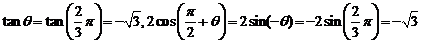 可知充分,
可知充分,
当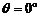 时
时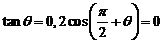 可知不必要.故选A
可知不必要.故选A
3、(山东文4)要得到函数 的图象,只需将函数
的图象,只需将函数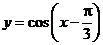 的图象( )
的图象( )
A.向右平移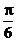 个单位 B.向右平移
个单位 B.向右平移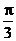 个单位
个单位
C.向左平移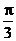 个单位 D.向左平移
个单位 D.向左平移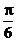 个单位
个单位
[答案]A[分析]: 本题看似简单,必须注意到余弦函数是偶函数。注意题中给出的函数不同名,而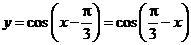
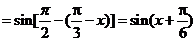 ,故应选A。
,故应选A。
2、(全国1理12)函数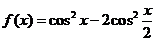 的一个单调增区间是
的一个单调增区间是
A.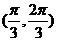 B.
B.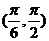 C.
C.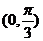 D.
D.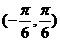
解.函数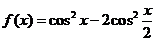 =
=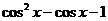 ,从复合函数的角度看,原函数看作
,从复合函数的角度看,原函数看作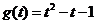 ,
,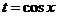 ,对于
,对于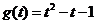 ,当
,当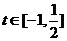 时,
时,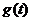 为减函数,当
为减函数,当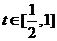 时,
时,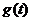 为增函数,当
为增函数,当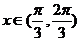 时,
时,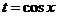 减函数,且
减函数,且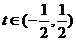 ,∴
原函数此时是单调增,选A。
,∴
原函数此时是单调增,选A。
1.(全国1理)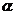 是第四象限角,
是第四象限角,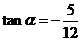 ,则
,则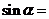
A. B.
B.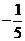 C.
C.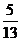 D.
D.
解.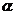 是第四象限角,
是第四象限角,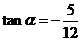 ,则
,则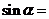 -
-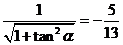
(三)解答题
1.(上海春卷17)已知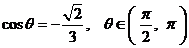 ,求
,求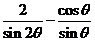 的值.
的值.
[解] 原式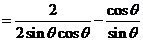
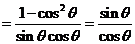 . …… 5分
. …… 5分
又 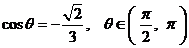 ,
,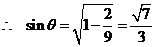
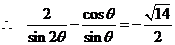 .
.
2.(安徽卷理17文17)已知函数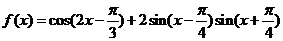
(Ⅰ)求函数 的最小正周期和图象的对称轴方程
的最小正周期和图象的对称轴方程
(Ⅱ)求函数 在区间
在区间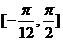 上的值域
上的值域
解:(1)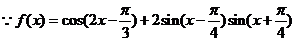
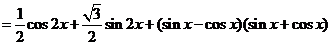
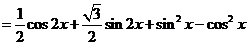
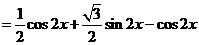
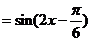
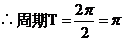
由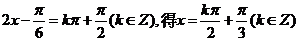
 函数图象的对称轴方程为
函数图象的对称轴方程为 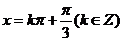
(2)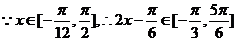
因为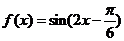 在区间
在区间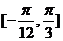 上单调递增,在区间
上单调递增,在区间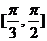 上单调递减,
上单调递减,
所以
当 时,
时, 取最大值 1
取最大值 1
又  ,当
,当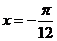 时,
时, 取最小值
取最小值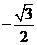
所以 函数  在区间
在区间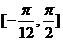 上的值域为
上的值域为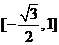
3.(北京卷理15文15)已知函数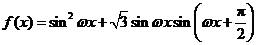 (
(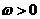 )的最小正周期为
)的最小正周期为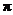 .(Ⅰ)求
.(Ⅰ)求 的值;(Ⅱ)求函数
的值;(Ⅱ)求函数 在区间
在区间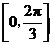 上的取值范围.
上的取值范围.
解:(Ⅰ)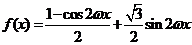
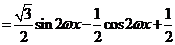
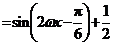 .
.
因为函数 的最小正周期为
的最小正周期为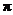 ,且
,且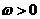 ,所以
,所以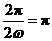 ,解得
,解得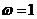 .
.
(Ⅱ)由(Ⅰ)得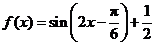 .
.
因为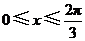 ,所以
,所以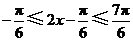 ,所以
,所以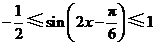 ,
,
因此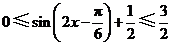 ,即
,即 的取值范围为
的取值范围为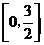 .
.
4.(广东卷理16文16)已知函数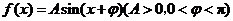 ,
,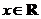 的最大值是1,其图像经过点
的最大值是1,其图像经过点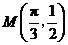 .(1)求
.(1)求 的解析式;(2)已知
的解析式;(2)已知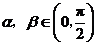 ,且
,且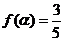 ,
,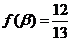 ,求
,求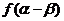 的值.
的值.
[解析](1)依题意有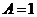 ,则
,则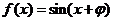 ,将点
,将点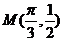 代入得
代入得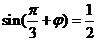 ,而
,而 ,
,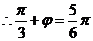 ,
,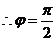 ,故
,故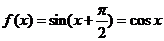 ;
;
(2)依题意有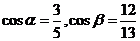 ,而
,而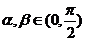 ,
,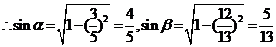 ,
,
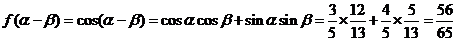 。
。
5.(湖北卷理16)已知函数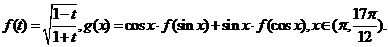 (Ⅰ)将函数
(Ⅰ)将函数 化简成
化简成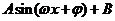 (
(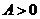 ,
,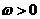 ,
,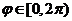 )的形式;(Ⅱ)求函数
)的形式;(Ⅱ)求函数 的值域.
的值域.
解.本小题主要考查函数的定义域、值域和三角函数的性质等基本知识,考查三角恒等变换、代数式的化简变形和运算能力.(满分12分)
解:(Ⅰ)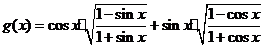
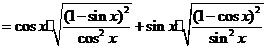
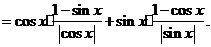
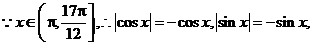
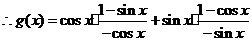
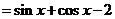 =
=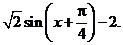
(Ⅱ)由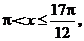 得
得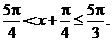
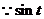 在
在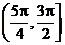 上为减函数,在
上为减函数,在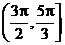 上为增函数,
上为增函数,
又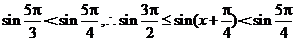 (当
(当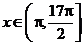 ),
),
即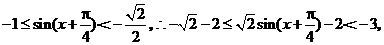 故g(x)的值域为
故g(x)的值域为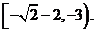
6.(湖北卷文16)已知函数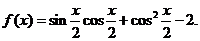 (Ⅰ)将函数
(Ⅰ)将函数 化简成
化简成
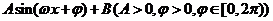 的形式,并指出
的形式,并指出 的周期; (Ⅱ)求函数
的周期; (Ⅱ)求函数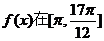 上的最大值和最小值
上的最大值和最小值
解:(Ⅰ)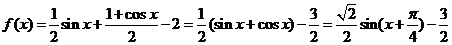 .
.
故 的周期为
的周期为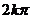 {k∈Z且k≠0}.
{k∈Z且k≠0}.
(Ⅱ)由π≤x≤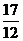 π,得
π,得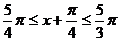 .因为f(x)=
.因为f(x)=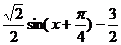 在[
在[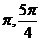 ]上是减函数,在[
]上是减函数,在[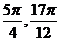 ]上是增函数.故当x=
]上是增函数.故当x=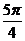 时,f(x)有最小值-
时,f(x)有最小值-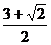 ;而f(π)=-2,f(
;而f(π)=-2,f(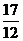 π)=-
π)=-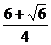 <-2,
<-2,
所以当x=π时,f(x)有最大值-2.
7.(湖南卷文17)已知函数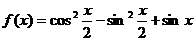 .
.
(I)求函数 的最小正周期;
的最小正周期;
(II)当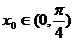 且
且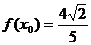 时,求
时,求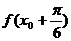 的值。
的值。
解:由题设有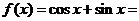
 .
.
(I)函数 的最小正周期是
的最小正周期是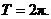
(II)由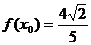 得
得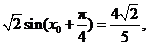 即
即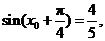
因为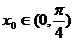 ,所以
,所以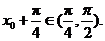
从而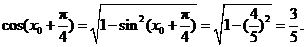
于是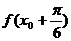
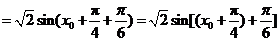
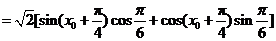
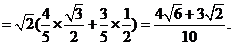
8.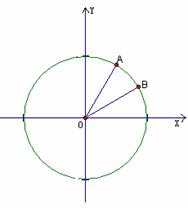 (江苏卷15).如图,在平面直角坐标系
(江苏卷15).如图,在平面直角坐标系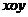 中,以
中,以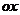 轴为始边做两个锐角
轴为始边做两个锐角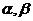 ,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为
,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为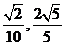 。
。
(1)
求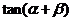 的值;
的值;
(2) 求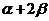 的值。
的值。
[试题解析]先由已知条件得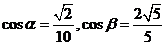 ,第(1)问求
,第(1)问求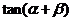 的值,运用正切的和角公式;第(2)问求
的值,运用正切的和角公式;第(2)问求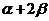 的值,先求出
的值,先求出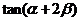 的值,再根据范围确定角的值。
的值,再根据范围确定角的值。
[标准答案](1)由已知条件即三角函数的定义可知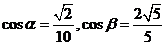 ,
,
因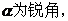 故
故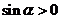 ,从而
,从而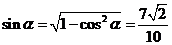
同理可得 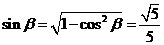 ,因此
,因此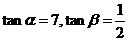 .
.
所以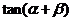 =
=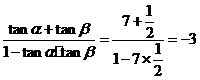 ;
;
(2)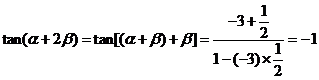 ,
,
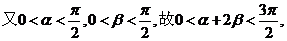
从而由 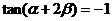 得
得 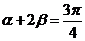 .
.
9.(江西卷文17)已知 ,
,
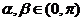
(1)求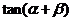 的值;
的值;
(2)求函数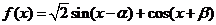 的最大值.
的最大值.
解:(1)由
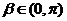 得
得 ,
,
于是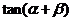 =
=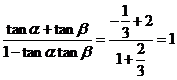 .
.
(2)因为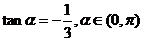 所以
所以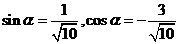


 的最大值为
的最大值为 .
.
10.(山东卷理17)已知函数f(x)=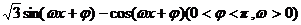 为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为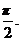 (Ⅰ)求f(
(Ⅰ)求f(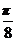 )的值;(Ⅱ)将函数y=f(x)的图象向右平移
)的值;(Ⅱ)将函数y=f(x)的图象向右平移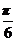 个单位后,再将得到的图象上各点的横坐标舒畅长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标舒畅长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
解:(Ⅰ)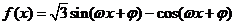
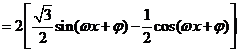
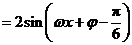 .因为
.因为 为偶函数,所以对
为偶函数,所以对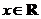 ,
,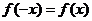 恒成立,
恒成立,
因此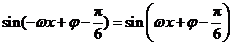 .
.
即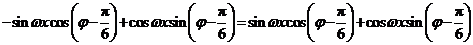 ,
,
整理得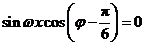 .因为
.因为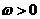 ,且
,且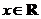 ,所以
,所以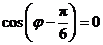 .
.
又因为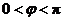 ,故
,故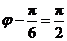 .所以
.所以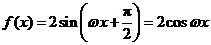 .
.
由题意得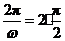 ,所以
,所以 .故
.故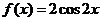 .因此
.因此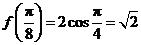 .
.
(Ⅱ)将 的图象向右平移
的图象向右平移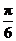 个单位后,得到
个单位后,得到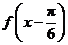 的图象,再将所得图象横坐标伸长到原来的4倍,纵坐标不变,得到
的图象,再将所得图象横坐标伸长到原来的4倍,纵坐标不变,得到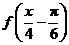 的图象.所以
的图象.所以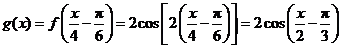 .
.
当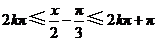 (
(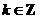 ),即
),即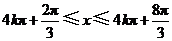 (
(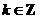 )时,
)时, 单调递减,
单调递减,
因此 的单调递减区间为
的单调递减区间为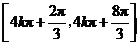 (
(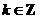 ).
).
11.(山东卷文17)已知函数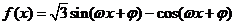 (
(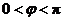 ,
,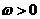 )为偶函数,且函数
)为偶函数,且函数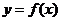 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为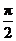 .(Ⅰ)求
.(Ⅰ)求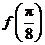 的值;(Ⅱ)将函数
的值;(Ⅱ)将函数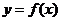 的图象向右平移
的图象向右平移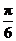 个单位后,得到函数
个单位后,得到函数 的图象,求
的图象,求 的单调递减区间.
的单调递减区间.
解:(Ⅰ)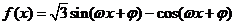
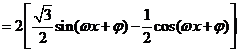
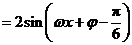 .
.
因为 为偶函数,所以对
为偶函数,所以对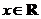 ,
,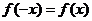 恒成立,
恒成立,
因此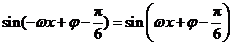 .
.
即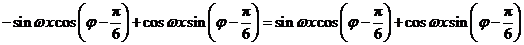 ,
,
整理得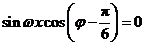 .因为
.因为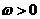 ,且
,且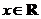 ,所以
,所以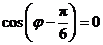 .
.
又因为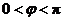 ,故
,故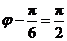 .所以
.所以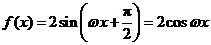 .
.
由题意得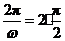 ,所以
,所以 .故
.故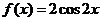 .因此
.因此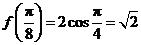 .
.
(Ⅱ)将 的图象向右平移
的图象向右平移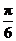 个单位后,得到
个单位后,得到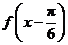 的图象,
的图象,
所以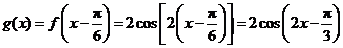 .
.
当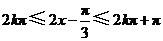 (
(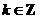 ),即
),即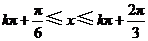 (
(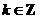 )时,
)时, 单调递减,
单调递减,
因此 的单调递减区间为
的单调递减区间为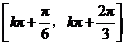 (
(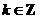 ).
).
12.(陕西卷理17)已知函数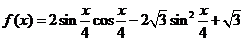 .(Ⅰ)求函数
.(Ⅰ)求函数 的最小正周期及最值;(Ⅱ)令
的最小正周期及最值;(Ⅱ)令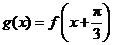 ,判断函数
,判断函数 的奇偶性,并说明理由.
的奇偶性,并说明理由.
解:(Ⅰ)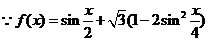
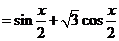
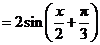 .
.
 的最小正周期
的最小正周期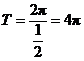 .
.
当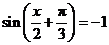 时,
时, 取得最小值
取得最小值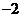 ;当
;当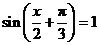 时,
时, 取得最大值2.
取得最大值2.
(Ⅱ)由(Ⅰ)知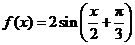 .又
.又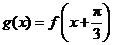 .
.
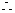
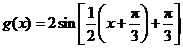
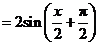
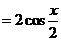 .
.
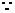
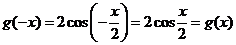 .
.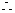 函数
函数 是偶函数.
是偶函数.
13.(陕西卷文17)已知函数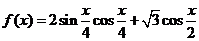 .(Ⅰ)求函数
.(Ⅰ)求函数 的最小正周期及最值;(Ⅱ)令
的最小正周期及最值;(Ⅱ)令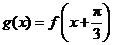 ,判断函数
,判断函数 的奇偶性,并说明理由.
的奇偶性,并说明理由.
解:(Ⅰ)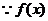
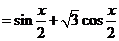
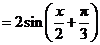 .
. 的最小正周期
的最小正周期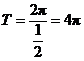 .
.
当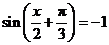 时,
时, 取得最小值
取得最小值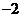 ;当
;当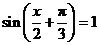 时,
时, 取得最大值2.
取得最大值2.
(Ⅱ)由(Ⅰ)知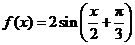 .又
.又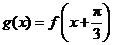 .
.
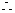
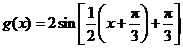
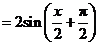
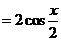 .
.
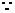
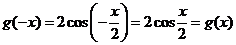 .
.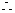 函数
函数 是偶函数.
是偶函数.
14.(上海卷文18)已知函数f(x)=sin2x,g(x)=cos(2x+),直线x=t(t∈R)与函数f(x)、g(x)的图像分别交于M、N两点⑴当t=时,求|MN|的值⑵求|MN|在t∈[0,]时的最大值
[解](1)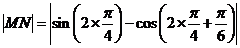 ….2分
….2分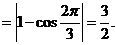 ………5分
………5分
(2)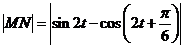
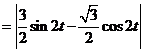
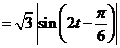 ……….11分
……….11分
∵ 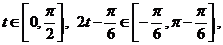 ∴ |MN|的最大值为
∴ |MN|的最大值为 . 15分
. 15分
15.(四川卷理17文17)求函数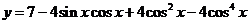 的最大值与最小值。
的最大值与最小值。
[解]: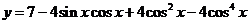
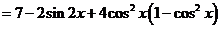
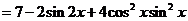
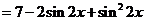
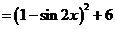
由于函数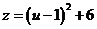 在
在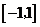 中的最大值为
中的最大值为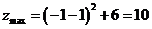 最小值为
最小值为
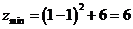 故当
故当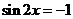 时
时 取得最大值
取得最大值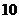 ,当
,当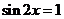 时
时 取得最小值
取得最小值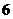
[点评]:此题重点考察三角函数基本公式的变形,配方法,符合函数的值域及最值;
[突破]:利用倍角公式降幂,利用配方变为复合函数,复合函数中间变量的范围是关键;
16.(天津卷理17)已知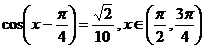 .(Ⅰ)求
.(Ⅰ)求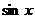 的值;(Ⅱ)求
的值;(Ⅱ)求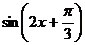 的值.
的值.
解:(Ⅰ)因为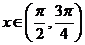 ,所以
,所以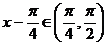 ,于是
,于是
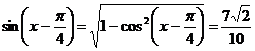
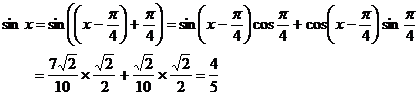
(Ⅱ)因为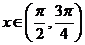 ,故
,故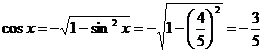
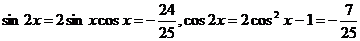
所以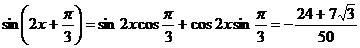
17.(天津卷文17)已知函数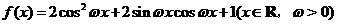 的最小正周期是
的最小正周期是 .(Ⅰ)求
.(Ⅰ)求 的值;(Ⅱ)求函数
的值;(Ⅱ)求函数 的最大值,并且求使
的最大值,并且求使 取得最大值的
取得最大值的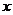 的集合.
的集合.
本小题主要考查特殊角三角函数值、两角和的正弦、二倍角的正弦与余弦、函数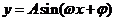 的性质等基础知识,考查基本运算能力.满分12分.
的性质等基础知识,考查基本运算能力.满分12分.
(Ⅰ)解: 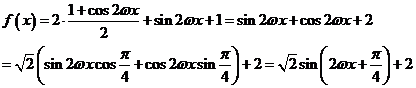
由题设,函数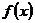 的最小正周期是
的最小正周期是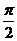 ,可得
,可得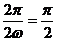 ,所以
,所以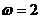 .
.
(Ⅱ)由(Ⅰ)知,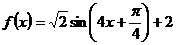 .
.
当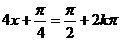 ,即
,即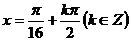 时,
时,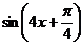 取得最大值1,所以函数
取得最大值1,所以函数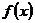 的最大值是
的最大值是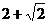 ,此时
,此时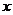 的集合为
的集合为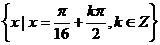 .
.
2007高考试题及解析
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com