
13.(江苏省南通市2008届高三第二次调研考试)在△ABC中,角A,B,C所对边分别为a,b,c,且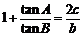 .
.
(Ⅰ)求角A;(Ⅱ)若m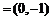 ,n
,n ,试求|m
,试求|m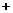 n|的最小值.
n|的最小值.
解:(Ⅰ) ,…3分
,…3分
即 ,∴
,∴ ,
,
∴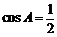 . ………5分∵
. ………5分∵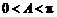 ,∴
,∴ .……7分
.……7分
(Ⅱ)m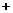 n
n 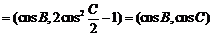 ,
,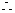 |m
|m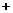 n|
n| . 10分
. 10分
∵ ,∴
,∴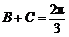 ,∴
,∴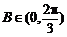 .从而
.从而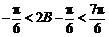 .………12分
.………12分
∴当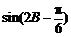 =1,即
=1,即 时,|m
时,|m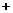 n|
n| 取得最小值
取得最小值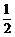 . 13分所以|m
. 13分所以|m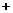 n|
n|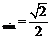 .……14分
.……14分
12.(常州市北郊中学2008届第一次模拟检测)已知向量a=(3sinα,cosα),b=(2sinα,
5sinα-4cosα),α∈(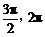 ),且a⊥b. (1)求tanα的值;
(2)求cos(
),且a⊥b. (1)求tanα的值;
(2)求cos(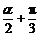 )的值.
)的值.
解:(1)∵a⊥b,∴a·b=0.而a=(3sinα,cosα),b=(2sinα, 5sinα-4cosα),
故a·b=6sin2α+5sinαcosα-4cos2α=0.
由于cosα≠0,∴6tan2α+5tanα-4 =0.解之,得tanα=- ,或tanα=
,或tanα=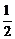 .
.
∵α∈(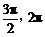 ),tanα<0,故tanα=
),tanα<0,故tanα=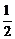 (舍去).∴tanα=-
(舍去).∴tanα=- .
.
(2)∵α∈(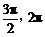 ),∴
),∴ .由tanα=-
.由tanα=- ,求得
,求得 ,
,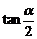 =2(舍去).
=2(舍去).
∴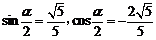 ,cos(
,cos( )=
)=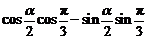
=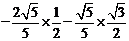 =
= .
.
11.(河北省正定中学2008年高三第五次月考)已知A、B、C的坐标分别为A(4,0),B(0,4),C( ).(Ⅰ)若
).(Ⅰ)若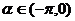 ,且
,且 ,求角
,求角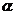 的大小;
的大小;
(Ⅱ)若 ,求
,求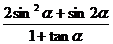 的值。
的值。
解、(Ⅰ)由已知得: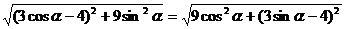
则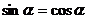 因为
因为
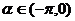
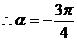 ……
…5分
……
…5分
(Ⅱ)由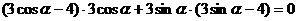
得 平方得
平方得  …..8分
…..8分
而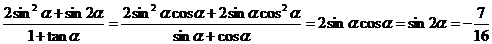 --10分
--10分
10.(河北衡水中学2008年第四次调考)已知向量=(cosx,sinx),=(,),若·=,且<x<,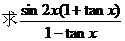 的值.
的值.
解: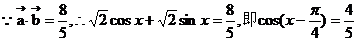 …………2分
…………2分
∵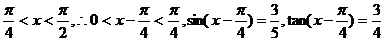 ……4分
……4分

 …6分
…6分
∴ 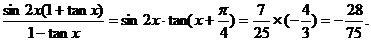 …………10分
…………10分
9.(贵州省贵阳六中、遵义四中2008年高三联考)已知函数f(x)=2sinxcosx+cos2x.
(Ⅰ)求f ( )的值; (Ⅱ)设
)的值; (Ⅱ)设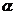 ∈(0,
∈(0,
 ),f (
),f (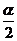 )=
)=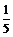 ,求cos2
,求cos2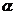 的值.
的值.
解:(Ⅰ)∵f(x)=sin2x+cos2x,∴f( )=sin
)=sin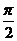 +cos
+cos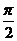 =1………5分
=1………5分
(Ⅱ)∵f( )=sinα+cosα=
)=sinα+cosα=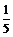 ,∴1+sin2α=
,∴1+sin2α= , sin2α=
, sin2α= ,……7分
,……7分
∴cos2α=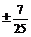 ∵α∈(0,
∵α∈(0, π)∴2α∈(π,
π)∴2α∈(π,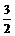 π) ∴cos2α<0.故cos2α=
π) ∴cos2α<0.故cos2α=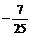 ……10分
……10分
8.(广东省2008届六校第二次联考)已知向量 ,
,  ,
, 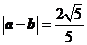 .
.
(Ⅰ)求 的值;(Ⅱ)若
的值;(Ⅱ)若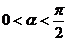 ,
,  , 且
, 且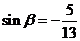 , 求
, 求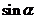 .
.
解:(Ⅰ) ,
,  ,
,
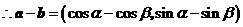 .
.
 ,
, 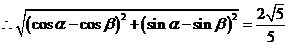 ,
,
即  ,
, 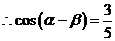 .
.
(Ⅱ)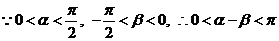 ,
,
 ,
,
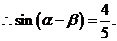
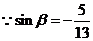 ,
, 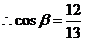 ,
,
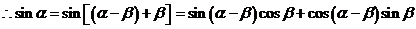
 .
.
7.(北京市十一学校2008届高三数学练习题)已知函数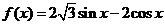 .
.
(Ⅰ)若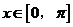 ,求
,求 的最大值和最小值;(Ⅱ)若
的最大值和最小值;(Ⅱ)若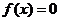 ,求
,求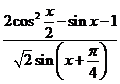 的值.
的值.
解:(Ⅰ) 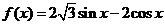

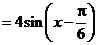 .…3分又
.…3分又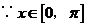 ,
, ,
, 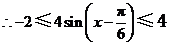 ,
,
 .…6分
.…6分
(II)由于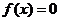 ,所以
,所以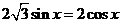 解得
解得 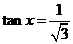 …8分
…8分
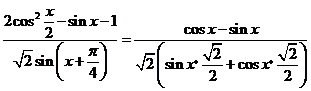
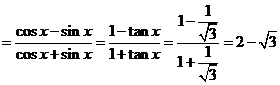
6.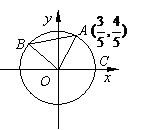 (2008广东高三地区模拟)如图A、B是单位圆O上的点,且
(2008广东高三地区模拟)如图A、B是单位圆O上的点,且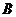 在第二象限. C是圆与
在第二象限. C是圆与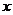 轴正半轴的交点,A点的坐标为
轴正半轴的交点,A点的坐标为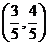 ,△AOB为正三角形.
,△AOB为正三角形.
(Ⅰ)求 ; (Ⅱ)求
; (Ⅱ)求 .
.
解:(1)因为A点的坐标为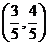 ,根据三角函数定义可知
,根据三角函数定义可知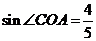 ---4分
---4分
(2)因为三角形AOB为正三角形,所以 ,
,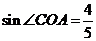 ,
,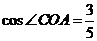 , -----6分
, -----6分
所以 =
=
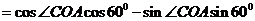 -----10分
-----10分
=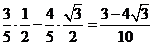 .--12分
.--12分
理(Ⅱ)求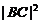 的值.
的值.
解:(Ⅱ)因为三角形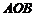 为正三角形,所以
为正三角形,所以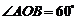 ,
,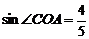 ,
, , ……5分
, ……5分
所以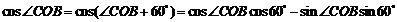
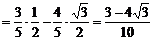 8分
8分
所以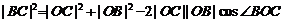
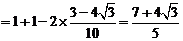 12分
12分
5.(2008年高三名校试题汇编)设 ,其
,其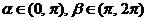 ,a与c的夹角为
,a与c的夹角为 ,b与c的夹角为
,b与c的夹角为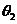 ,且
,且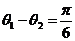 ,求
,求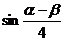 的值.
的值.
解 a=(2cos2 ,2sin
,2sin cos
cos )=2cos
)=2cos (cos
(cos ,sin
,sin ),
),
b=(2sin2 ,2sin
,2sin cos
cos )=2sin
)=2sin (sin
(sin ,cos
,cos ),
),
∵α∈(0,π),β∈(π,2π), ∴ ∈(0,
∈(0, 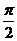 ),
), ∈(
∈(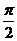 ,π),故|a|=2cos
,π),故|a|=2cos ,|b|=2sin
,|b|=2sin ,
,
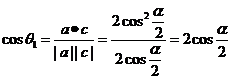 ,
,
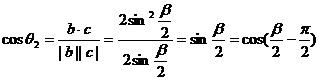 ,∵0<
,∵0< <
<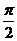 ,∴
,∴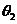 =
= ,又
,又 -
-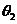 =
= ,∴
,∴ -
- +
+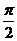 =
= ,故
,故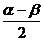 =-
=- ,∴sin
,∴sin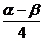 =sin(-
=sin(- )=-
)=- .
.
4.(广东2008年01月份期末试题)已知向量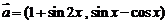 ,
,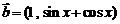 ,函数
,函数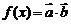 .(Ⅰ)求
.(Ⅰ)求 的最大值及相应的
的最大值及相应的 的值;(Ⅱ)若
的值;(Ⅱ)若 ,求
,求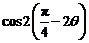 的值.
的值.
解:(Ⅰ)因为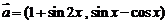 ,
,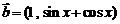 ,所以
,所以
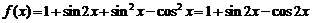
 .
.
因此,当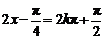 ,即
,即 (
(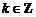 )时,
)时, 取得最大值
取得最大值 ;
;
(Ⅱ)由 及
及 得
得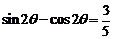 ,两边平方得
,两边平方得
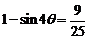 ,即
,即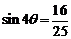 .因此,
.因此,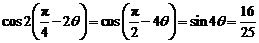 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com