
5、己知函数f(x)=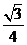 sin x一
sin x一 cos x。 (1)若cosx=-
cos x。 (1)若cosx=-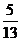 ,x
,x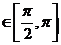 ,求函数f (x)的值; (2)将函数f(x)的图像向右平移m个单位,使平移后的图像关于原点对称,
,求函数f (x)的值; (2)将函数f(x)的图像向右平移m个单位,使平移后的图像关于原点对称,
若0<m< ,试求m的值。
,试求m的值。
解:(1)因为cos=-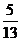 ,x
,x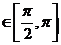 ,所以,sinx=
,所以,sinx=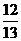
所以,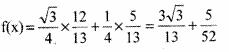
(2)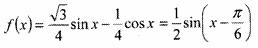 ,
,
所以,把f(x)的图象向右平移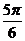 个单位,得到,y=-
个单位,得到,y=- sinx的图象,其图象关于原点对称。
sinx的图象,其图象关于原点对称。
故m=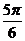
4、设函数 将函数
将函数 的图象向左平移
的图象向左平移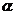 个单位,得到函数
个单位,得到函数 的图象。(1)求函数
的图象。(1)求函数 的最小正周期;(2)若
的最小正周期;(2)若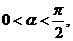 且
且 是偶函数,求
是偶函数,求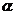 的值。
的值。
解: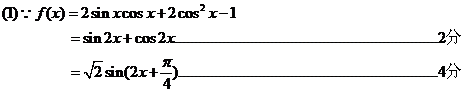
3、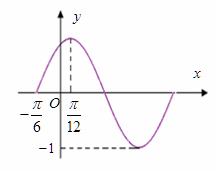 已知函数
已知函数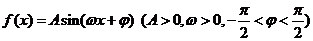 一个周期的图象如图所示,(1)求函数
一个周期的图象如图所示,(1)求函数 的表达式;
的表达式;
(2)若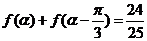 ,且
,且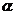 为
为 的一个内角,
的一个内角,
求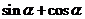 的值.
的值.
解:(1)从图知,函数的最大值为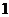 ,则
,则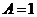 1分
1分
函数 的周期为
的周期为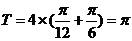 , 2分
, 2分
而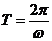 ,则
,则 , ……3分又
, ……3分又 时,
时,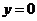 ,∴
,∴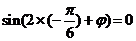 ,
而
,
而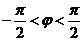 ,则
,则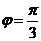 ,…5分∴函数
,…5分∴函数 的表达式为
的表达式为
 … 6分
… 6分
(2)由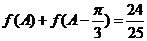 得:
得:
化简得: ,… 8分∴
,… 8分∴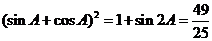 …… 9分
…… 9分
由于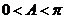 ,则
,则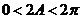 ,但
,但 ,则
,则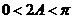 ,即A为锐角,
,即A为锐角,
从而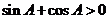 ……11分因此
……11分因此 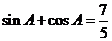 .
…… 12分
.
…… 12分
2、在 中,已知
中,已知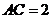 ,
,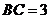 ,
,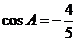 .
.
(1)求 的值;(2)求
的值;(2)求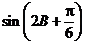 的值.
的值.
解:(1)由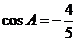 可得
可得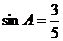 所以由正弦定理可得
所以由正弦定理可得  =
=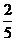
(2)由已知可知A为钝角,故得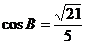
从而  ,
,
所以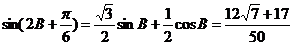
1、已知△ABC的内角A、B、C所对的边分别为a,b,c,且a=2, cosB=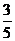 .
.
(1)若b=4,求sinA的值; (2) 若△ABC的面积S△ABC=4,求b,c的值.
解:(1) ∵cosB=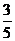 >0,且0<B<π,∴sinB=
>0,且0<B<π,∴sinB=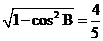 . ……2分
. ……2分
由正弦定理得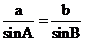 ,…4分
,…4分 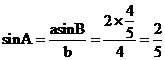 . ……6分
. ……6分
(2) ∵S△ABC= acsinB=4,8分
∴
acsinB=4,8分
∴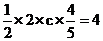 , ∴c=5. …10分
, ∴c=5. …10分
由余弦定理得b2=a2+c2-2accosB,∴ .14分
.14分
8.设函数 有以下结论:
有以下结论:
①点(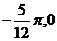 )是函数
)是函数 图象的一个对称中心;
图象的一个对称中心;
②直线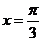 是函数
是函数 图象的一条对称轴;
图象的一条对称轴;
③函数 的最小正周期是
的最小正周期是 ;
;
④将函数 的图象向右平移
的图象向右平移 个单位后,对应的函数是偶函数。
个单位后,对应的函数是偶函数。
其中所有正确结论的序号是 。
答案:(②③④ )
7.已知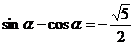 ,则
,则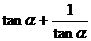 的值为_ _
的值为_ _
答案:(-8 )
6.已知定点A(4,2),O是坐标原点,P是线段OA的垂直平分线 上一点,若∠OPA为钝角,那么点P的横坐标的取值范围是
答案:((1,2) (2,3)
(2,3)
5.把函数 的图像向右平移
的图像向右平移 个单位,再把所得图像上各点的横坐标缩短为原来的
个单位,再把所得图像上各点的横坐标缩短为原来的 (纵坐标不变),则所得图像的解析式为
(纵坐标不变),则所得图像的解析式为
答案:( )
)
4.(宁夏09)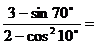 .
.
答案:(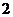 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com