
8.已知函数f(x)在[0, +∞)上是增函数,g(x)=-f(|x|),若g(lgx)>g(1),则x的取值范围是 ( )
(A).(0, 10) (B).(10, +∞)
(C).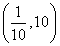 (D).
(D).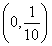 ∪(10,+∞)
∪(10,+∞)
7.设a=log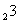 , b=
, b=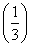
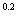 ,c=
,c=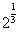 ,
,
则 ( )
(A).a<b<c (B).c<b<a (C).c<a<b (D).b<a<c
6.方程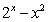 =0的解的个数是
( )
=0的解的个数是
( )
(A).1 (B).2 (C).3 (D).4
5.已知函数f(x)=lg(x+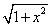 ),若f(a)=b,则f(-a)=
( )
),若f(a)=b,则f(-a)=
( )
(A).b
(B).-b
(C).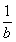 (D).-
(D).-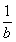
4.设f(x)=4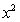 -mx+5在区间(-∞,-2]上是减函数,则f(1)的取值范围是
( )
-mx+5在区间(-∞,-2]上是减函数,则f(1)的取值范围是
( )
(A).f(1)>25 (B).f(1)=25 (C).f(1)≥25 (D)f(1)≤25
3.函数f(x)=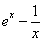 的零点所在的区间是
( ).
的零点所在的区间是
( ).
(A).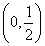 (B).
(B).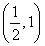 (C).
(C).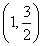 (D).
(D).
2.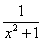 设f(x)=
设f(x)=
, |x|>1,
则f[f(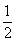 )]=
( )
)]=
( )
(A). 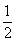 (B).
(B). 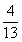 (C).
-
(C).
-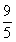 (D).
(D). 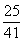
1.若A为全体正实数的集合,B={-2,-1,1,2},则下列结论中正确的是 ( )
(A).A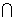 B={-2,-1} (B).(
B={-2,-1} (B).(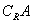 )
)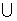 B=(-
B=(- ,0)
,0)
(C).A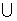 B=(0,+
B=(0,+ ) (D).(
) (D).(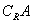 )
)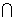 B={-2,-1}
B={-2,-1}
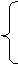 |x-1|-2, |x|
|x-1|-2, |x|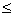 1,
1,
2.(2009山东卷理)(本小题满分12分)两县城A和B相距20km,现计划在两县城外以AB为直径的半圆弧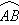 上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k ,当垃圾处理厂建在
上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k ,当垃圾处理厂建在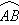 的中点时,对城A和城B的总影响度为0.065.(1)将y表示成x的函数;(11)讨论(1)中函数的单调性,并判断弧
的中点时,对城A和城B的总影响度为0.065.(1)将y表示成x的函数;(11)讨论(1)中函数的单调性,并判断弧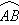 上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由。
上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由。
解法一:(1)如图,由题意知AC⊥BC,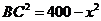 ,
,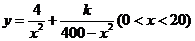
 其中当
其中当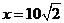 时,y=0.065,所以k=9
时,y=0.065,所以k=9
所以y表示成x的函数为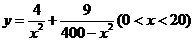
(2)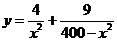 ,
,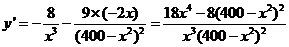 ,令
,令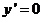 得
得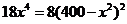 ,所以
,所以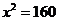 ,即
,即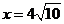 ,当
,当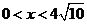 时,
时, 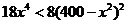 ,即
,即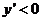 所以函数为单调减函数,当
所以函数为单调减函数,当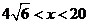 时,
时, 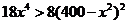 ,即
,即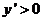 所以函数为单调增函数.所以当
所以函数为单调增函数.所以当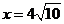 时, 即当C点到城A的距离为
时, 即当C点到城A的距离为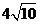 时, 函数
时, 函数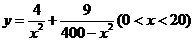 有最小值.
有最小值.
解法二: (1)同上.
(2)设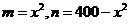 ,则
,则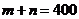 ,
,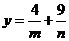 ,所以
,所以
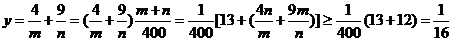 当且仅当
当且仅当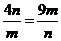
即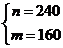 时取”=”.下面证明函数
时取”=”.下面证明函数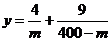 在(0,160)上为减函数, 在(160,400)上为增函数.
在(0,160)上为减函数, 在(160,400)上为增函数.
设0<m1<m2<160,则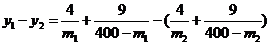
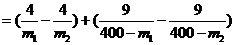
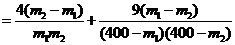
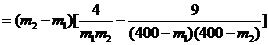
1.设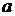 为实数,函数
为实数,函数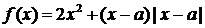 . (1)若
. (1)若 ,求
,求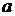 的取值范围; (2)求
的取值范围; (2)求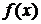 的最小值; (3)设函数
的最小值; (3)设函数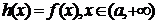 ,直接写出(不需给出演算步骤)不等式
,直接写出(不需给出演算步骤)不等式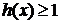 的解集.
的解集.
[解析]本小题主要考查函数的概念、性质、图象及解一元二次不等式等基础知识,考查灵活运用数形结合、分类讨论的思想方法进行探索、分析与解决问题的综合能力。满分16分
(1)若 ,则
,则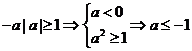
(2)当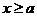 时,
时,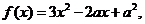
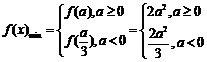
当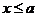 时,
时,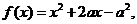

综上
(3)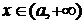 时,
时,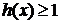 得
得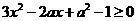 ,
,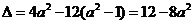
当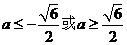 时,
时,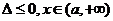 ;
;
当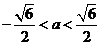 时,△>0,得:
时,△>0,得: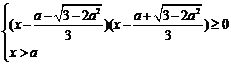
讨论得:当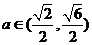 时,解集为
时,解集为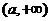 ;
;
当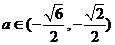 时,解集为
时,解集为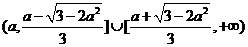 ;
;
当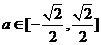 时,解集为
时,解集为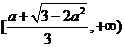 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com