5．晶胞是晶体结构中最小的　　　 　　　　　　，是从晶体结构中截取下来的大小、形状完全相同的　　　　　　　 。

4．金属晶体的结构形式可归结为等径圆球的密堆积。其中，每一层都是最紧密堆积，也就是每个等径球与周围　　　　　　　　 相接触。而层与层之间的堆积时有多种方式：

一种是“…ABAB…”重复方式，叫　　　 型的最密堆积，一种是“…ABCABC…” 重复方式，叫　　　　 型的最密堆积。

3．因为金属键、离子键、分子间的相互作用没有　　　　　　　　　 ，所以组成金属晶体、离子晶体、分子晶体的微粒服从　　　　　　　　　 原理。

2．　　 　　　　　　　　　的晶体称为离子晶体；　　　 　　　　　　　的晶体称为金属晶体；

　　　　　 　　　　　　　　的晶体称为原子晶体；　　　　　　　　 　　　的晶体称为分子晶体。

1．晶体的特性是　　　　　　　　　　　　　　　　　　　　　　　　　 。

3．知道晶胞是晶体的最小结构重复单元，能用切割法计算一个晶胞种实际拥有的微粒数。

[自学助手]

2．了解A₁、A₃ 型密堆积。

1．能区分晶体与非晶体，知道晶体的重要特征。

61．如图所示，一辆质量m = 2 kg的平板车左端放在质量M = 3 kg的小滑块，滑块与平板车之间的动摩擦因数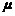= 0.4。开始时平板车和滑块共同以v₀ = 2 m/s的速度在光滑水平面上向右运动，并与竖直墙壁发生碰撞，设碰撞时间极短，且碰撞后平板车速度大小保持不变，但方向与原来相反。平板车足够长，以至滑块不会滑到平板车右端(取g = 10 m/s²)求：

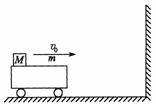
　 (1)平板车第一次与墙壁碰撞后向左运动的最大距离；

　 (2)为使滑块始终不会滑到平板车右端，平板车至少为多长？

　 答案：(1)设平板车第一次碰墙后，平板车左移的距离为s，速度变为0。由于系统总动量向右，平板车速度为零时，滑块还在向右滑行。由动能定理知

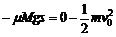　　　 　 得s =

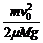
　　　 代入数据得s =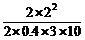m = 0.33 m

　 (2)平板车与墙壁发生多次碰撞后将停在墙边。设滑块相对平板车的总位移为L，则有：

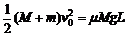
　　　 解得L =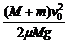

　　　 代入数据得L = 0.833 m

　　　 即为平板车的最短长度

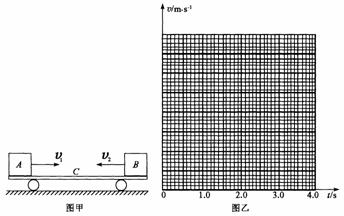
60．质量为M = 3.0 kg的平板小车C静止在光滑水平面上，如图甲所示。当t = 0时，两个质量都为m = 1.0 kg的小物体A和B，分别从小车的左端和右端的以水平速度v₁ = 4.0 m/s和v₂ = 2.0 m/s冲上小车，当它们在车上停止滑动时，没有相碰。A、B与车面的动摩擦因数都是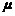= 0.20，g取10 m/s²。求：

　 (1)A、B在车上停止滑动时车的速度。

　 (2)车的长度至少是多少？

　 (3)在图乙所给出的坐标系中画出0至0.4 s内小车运动的速度-时间图象。

　 答案：(1)设A、B在车上停止滑动时，车的速度为v，以向右为正方向，根据动量守恒定律，

　　　 m (v₁ – v₂) = (M + 2m) v，

　　　 解得v = 0.40 m/s，方向水平向右。

　 (2)设A、B在车上相对于车滑动的距离分别为l₁和l₂，由功能关系知

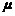　　　 mgl₁ +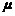mgl₂ =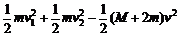

　　　 解得：l₁ + l₂ = 4.8 m

　　　 即车长至少为4.8 m

　 (3)车的运动可分以下三个阶段：

　　　 第一阶段：A、B同时在车上滑行时，物体对车的摩擦力均为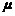mg，方向相反，车受平衡力作用而保持不动，当B的速度为零时，此过程结束，设这段时间内物体的加速度为a，根据牛顿第二定律知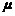mg = ma

　　　 得滑块的加速度a =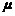g

　　　 物体B停止滑动的时间为t₁ =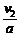= 1.0 s

　　　 第二阶段：B停止运动后，A继续在车上滑动，设到t₂时刻物体与车有共同速度v，则

　　　 v = (v₁ – t₂) – a (t₂ – t₁)

　　　 解得　 t₂ = 1.8 s

　　　 第三阶段：经过t₂时间之后，车以速度v做匀速直线运动直到t = 4.0 s为止，图象略。