
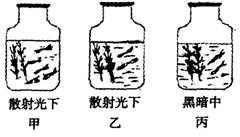
3.某生物兴趣小组的同学用河水、池泥、水藻、植食性小鱼、广口瓶、凡士林等材料制作了3个生态瓶(如上图(右)所示)。下列说法中错误的是
A.甲瓶中的小鱼很快死亡是因为瓶内分解者数量过少
B.乙瓶中的生物存活的时间相对较长
C.丙瓶中的分解者主要存在于河水及池泥中
D.若想维持生态平衡,丙瓶不应放在黑暗中
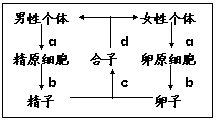
2.下图(左)中a、b、c、d表示人的生殖周期中不同的生理过程。下列说法正确的是:
A.a、b、c、d均能发生基因重组
B.基因重组主要是通过c和d来实现的
C.b和a的主要相同点之一是染色体在分裂过程移向两极
 D.d和b的主要差异之一是姐妹染色单体的分离
D.d和b的主要差异之一是姐妹染色单体的分离
1.下面与水相关的叙述不正确的是:
A.水是生化反应的介质
B.核糖体中进行的化学反应要脱水
C.线粒体中没有水的分解,但有水的生成
D.越冬或休眠的植物体内自由水与结合水的比值下降
21. 证(1)由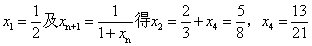
由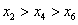 猜想:数列
猜想:数列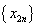 是递减数列
是递减数列
下面用数学归纳法证明:
(1)当n=1时,已证命题成立 (2)假设当n=k时命题成立,即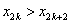
易知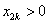 ,那么
,那么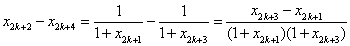
=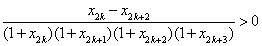
即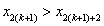
也就是说,当n=k+1时命题也成立,结合(1)和(2)知,命题成立
(2)当n=1时,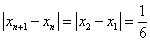 ,结论成立
,结论成立
当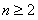 时,易知
时,易知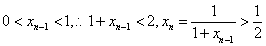
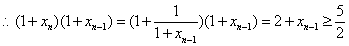
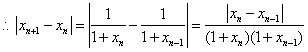
20.[解法1]本题主要考查双曲线的标准方程、圆的切线方程等基础知识,考查曲线和方程
的关系等解析几何的基本思想方法,考查推理、运算能力.
(Ⅰ)由题意,得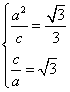 ,解得
,解得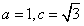 ,
,
∴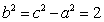 ,∴所求双曲线
,∴所求双曲线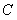 的方程为
的方程为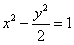 .
.
(Ⅱ)点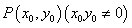 在圆
在圆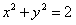 上,
上,
圆在点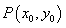 处的切线方程为
处的切线方程为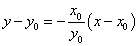 ,
,
化简得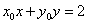 .
.
由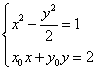 及
及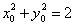 得
得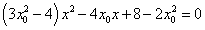 ,
,
∵切线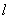 与双曲线C交于不同的两点A、B,且
与双曲线C交于不同的两点A、B,且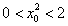 ,
,
∴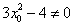 ,且
,且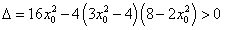 ,
,
设A、B两点的坐标分别为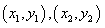 ,
,
则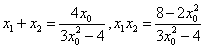 ,
,
∵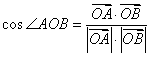 ,且
,且
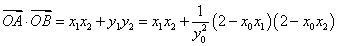 ,
,
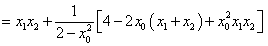
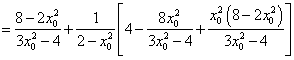
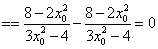 .
.
∴ 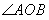 的大小为
的大小为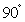 .
.
[解法2](Ⅰ)同解法1.
(Ⅱ)点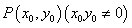 在圆
在圆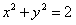 上,
上,
圆在点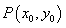 处的切线方程为
处的切线方程为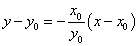 ,
,
化简得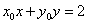 .由
.由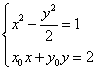 及
及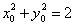 得
得
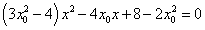 ①
①
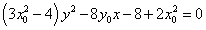 ②
②
∵切线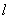 与双曲线C交于不同的两点A、B,且
与双曲线C交于不同的两点A、B,且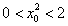 ,
,
∴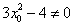 ,设A、B两点的坐标分别为
,设A、B两点的坐标分别为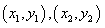 ,
,
则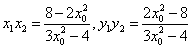 ,
,
∴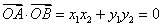 ,∴
,∴ 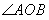 的大小为
的大小为 .
.
(∵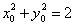 且
且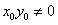 ,∴
,∴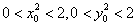 ,从而当
,从而当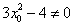 时,方程①和方程②的判别式均大于零).
时,方程①和方程②的判别式均大于零).
19. (本小题满分14分)
(本小题满分14分)
解 (Ⅰ)设需要新建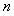 个桥墩,
个桥墩,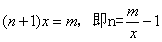
所以 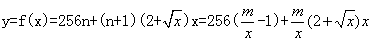
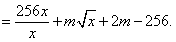
(Ⅱ) 由(Ⅰ)知,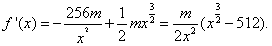
令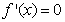 ,得
,得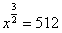 ,所以
,所以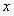 =64
=64
当0<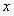 <64时
<64时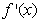 <0,
<0, 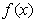 在区间(0,64)内为减函数;
在区间(0,64)内为减函数;
当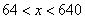 时,
时,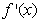 >0.
>0. 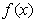 在区间(64,640)内为增函数,
在区间(64,640)内为增函数,
所以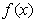 在
在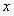 =64处取得最小值,此时,
=64处取得最小值,此时,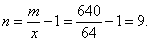
故需新建9个桥墩才能使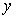 最小。
最小。
17.解 (1)设事件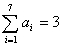 为A,则在7次抛骰子中出现5次奇数,2次偶数
为A,则在7次抛骰子中出现5次奇数,2次偶数
而抛骰子出现的奇数和偶数的概率为P是相等的,且为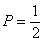 …………3分(未设、末设P,扣此3分)
…………3分(未设、末设P,扣此3分)
根据独立重复试验概率公式: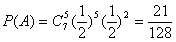 ………………6分
………………6分
(2)若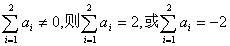
即前2次抛骰子中都是奇数或都是偶数.
若前2次都是奇数,则必须在后5次中抛出3次奇数2次偶数,
其概率: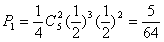 …………………………………………8分
…………………………………………8分
若前2次都是偶数,则必须在后5次中抛出5次奇数,其概率:
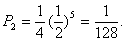 …………………………………………………………10分
…………………………………………………………10分
 所求事件的概率
所求事件的概率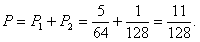 …………………………12分
…………………………12分
16. (Ⅰ)解: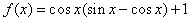
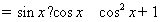
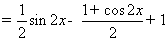 ---------2分
---------2分
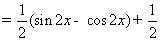
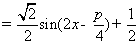 ,
--------4分
,
--------4分
因为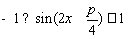 (其中
(其中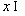 R),
R),
所以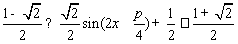 ,即函数
,即函数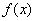 的值域为
的值域为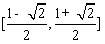 . -----6分
. -----6分
函数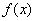 的对称中心为
的对称中心为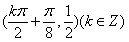 .
-------------------------8分
.
-------------------------8分
(Ⅱ)解:由(Ⅰ)得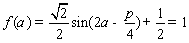 ,所以
,所以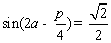 ,
------10分
,
------10分
因为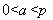 ,所以
,所以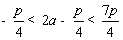 ,
------11分
,
------11分
所以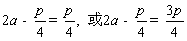 ,所以
,所以 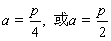 .------- ----------14分
.------- ----------14分
15.解析:
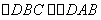 ,
,
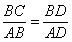
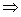
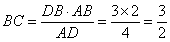
14.解析:问题等价于圆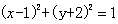 与直线
与直线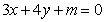 无公共点,则圆心
无公共点,则圆心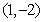 到直线
到直线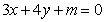 的距离
的距离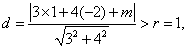 解得
解得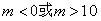
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com