
8. 数列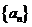 的首项
的首项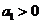 ,公比
,公比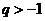 且
且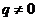 的等比数列,设数列
的等比数列,设数列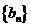 的通项
的通项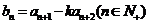 ,
,
数列的前n项之和分别为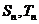 ,如果存在常数k,使得对所有的适合条件的两个数列,均有
,如果存在常数k,使得对所有的适合条件的两个数列,均有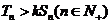
恒成立,试求实数k的取值范围 .
7. 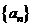 为等差数列且公差
为等差数列且公差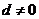 ,
,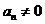
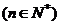 .一组方程
.一组方程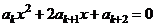
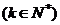 .
.
(1)求证: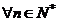 ,这组方程总有公共根.
,这组方程总有公共根.
(2)若各方程的不同的根依次为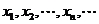 .求证:
.求证: 成等差数列 .
成等差数列 .
6. 给定正整数n和正数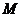 .对满足条件
.对满足条件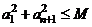 的所有等差数列
的所有等差数列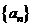 ,求
,求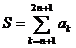 的最大值.
的最大值.
5. 等差数列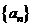 中公差
中公差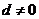 ,
,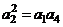 .若
.若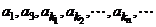 成等比数列,求
成等比数列,求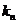 .
.
4. 等差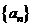 ,
,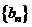 的前n项和分别为
的前n项和分别为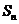 ,
,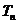 ,若
,若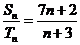 ,求:
,求:
(1) 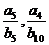 的值; (2) 是否存在正整数n使
的值; (2) 是否存在正整数n使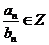 . 若存在,求出所有的n .
. 若存在,求出所有的n .
3.(1)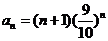 ,求数列
,求数列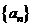 中的最大项.
中的最大项.
(2)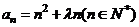 ,若
,若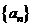 为单调递增的数列,求实数
为单调递增的数列,求实数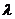 的取值范围.
的取值范围.
(3)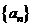 为等差数列,
为等差数列, 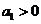 且
且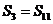 ,求:n为何值时
,求:n为何值时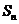 最大 .
最大 .
2. (1) 设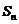 是数列
是数列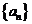 的前n项之和,而
的前n项之和,而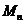 是数列
是数列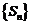 的前n项之和,且
的前n项之和,且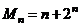 . 求:
. 求: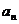 .
.
(2) 各项均为实数的等比数列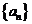 的前n项和记为
的前n项和记为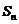 ,若
,若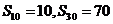 ,则
,则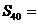 ________ .
________ .
1. 写出下列数列的一个通项公式: (1) 0,1,0,1,0,1,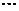 (2) 9,-99,999,-9999,
(2) 9,-99,999,-9999,
4. 补充:(1) 若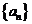 为等差数列,则
为等差数列,则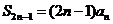 (相当于前
(相当于前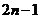 项的平均值为
项的平均值为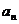 )
)
(2)
3. 等差,等比数列:
|
|
等差数列 |
等比数列 |
|
|
定义式 |
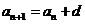 ; ;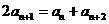 |
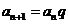 ; ;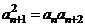 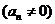 |
|
|
通项公式 |
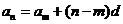 |
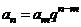 |
|
|
前n项和公式 |
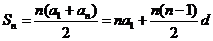 |
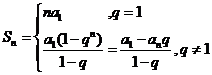 |
|
|
基 本 性 质 |
单调性 |
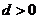 时, 时,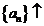 ; ;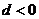 时, 时,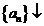 |
|
|
角标和 |
|
|
|
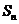 性质 性质 |
|
|
|
|
判定方法 |
(1) 定义 ; (2) 若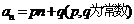 (3) 若 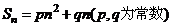 |
(1) 定义 (2) 若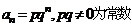 (3)若 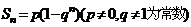 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com