
7. 等差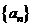 ,
,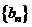 的前n项和分别为
的前n项和分别为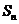 ,
,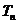 ,若
,若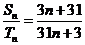 ,求:
,求:
(1) 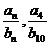 的值;
(2) 使
的值;
(2) 使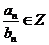 成立的所有正整数n .
成立的所有正整数n .
6. 给定正数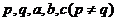 ,若
,若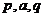 成等比,
成等比,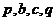 成等差,则二次方程
成等差,则二次方程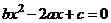 有( )
有( )
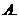 无实根
无实根 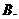 有两个相等实根
有两个相等实根 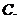 有两个同号相异实根
有两个同号相异实根 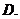 有两个异号相异实根
有两个异号相异实根
5. 给定正整数n,.对满足条件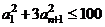 的所有等差数列
的所有等差数列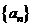 ,求
,求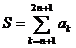 的最大值.
的最大值.
4. (1) 若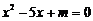 与
与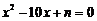 的四个实根适当排列后,组成一个首项为1的等比数列, 则
的四个实根适当排列后,组成一个首项为1的等比数列, 则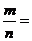 ____
____
(2) 正数项列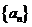 中,
中,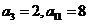 ,且
,且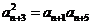 ,则
,则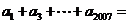 ___ .
___ .
(3) 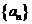 是等差,
是等差,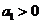 ,且
,且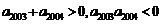 , 则使
, 则使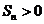 成立的最大自然数n是________
成立的最大自然数n是________
3. (1)已知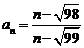
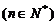 ,求数列
,求数列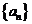 中的最大项和最小项.
中的最大项和最小项.
(2)若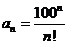 ,求数列
,求数列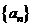 中的最大项.
中的最大项.
(3)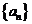 为等差数列,
为等差数列, 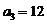 且
且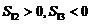 ,求:n为何值时
,求:n为何值时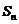 最大 .
最大 .
(4)等比数列满足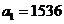 ,公比
,公比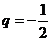 ,则该数列的前n项之积
,则该数列的前n项之积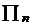 中最大的是第几项.
中最大的是第几项.
2. (1)已知不超过2000的正整数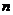 能表示成不少于60个连续正整数之和,这样的n有_________ 个 .
能表示成不少于60个连续正整数之和,这样的n有_________ 个 .
(2)设等差数列的首项及公差均为非负整数,项数不少于3,且各项的和为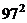 ,则这样的数列共有______个
,则这样的数列共有______个
(3)在公比大于1的等比数列中,最多有多少项是区间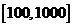 中的整数 .
中的整数 .
1. 写出下列数列的一个通项公式: (1) 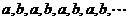 (2) 7,-77,777,-7777,77777,
(2) 7,-77,777,-7777,77777,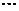
11. 数列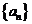 的相邻两项
的相邻两项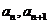 是方程
是方程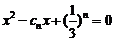 的两个根,且
的两个根,且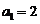 . 求数列
. 求数列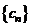 的前n项和
的前n项和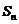
10. 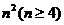 个正数排成n行n列的方阵(如右图):其中每一行
个正数排成n行n列的方阵(如右图):其中每一行
的数成等差数列,每一列的数成等比数列,并且所有的共比相等,
已知: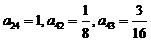 . 求:
. 求:
(1) 第i行第j列交汇处的数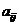 ;(2)
;(2) 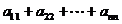 的值.
的值.
9. 求证:任意一个等比数列中至多有两项为质数. 并利它判断是否存在12个等比数列,使1,2,3,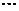 ,100分别为这12
,100分别为这12
个数列的项.
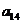
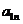
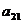
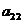
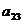
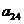
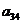
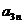
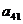
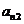
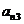
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com