
4. 有8种物质:①甲烷②乙烯③苯④聚乙烯⑤丙炔⑥环己烷⑦邻二甲苯⑧环己烯,其中既能使酸性高锰酸钾溶液褪色又能与溴水反应使之褪色的是( )
A.②④⑤⑧ B.②⑤⑧ C.②④⑤⑦ D.②⑤⑦⑧
3.分子式为C5H11Cl且只含3个甲基的同分异构体有( )
A.2种 B.3种 C.5种 D.4种
2.下列操作达不到预期目的的是( )
① 石油分馏时把温度计插入受热的液体中; ② 用酸性高锰酸钾溶液除去乙炔中含有的H2S;③ 用乙醇和3%的硫酸共热到170℃制取乙烯; ④ 将苯和溴水混合后加入铁粉制取溴苯;⑤ 将敞口久置的电石与蒸馏水混合制乙炔
A.只有①⑤ B.只有③④⑤ C.只有①②③⑤ D.①②③④⑤
1.下列说法正确的是( )
A.石油裂解可以得到氯乙烯 B.乙烯的结构简式可以表示为CH2CH2
C.甲烷和乙烯都可以与氯气反应 D.高锰酸钾可以氧化苯和甲苯
例4. 用轻弹簧相连的质量均为2kg的A、B两物块都以 的速度在光滑的水平地面上运动,弹簧处于原长,质量为4kg的物体C静止在前方,如图3所示,B与C碰撞后二者粘在一起运动。求:在以后的运动中,
的速度在光滑的水平地面上运动,弹簧处于原长,质量为4kg的物体C静止在前方,如图3所示,B与C碰撞后二者粘在一起运动。求:在以后的运动中,
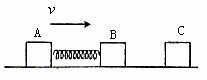
图3
(1)当弹簧的弹性势能最大时物体A的速度多大?
(2)弹性势能的最大值是多大?
(3)A的速度有可能向左吗?为什么?
解析:(1)当A、B、C三者的速度相等时弹簧的弹性势能最大,由于A、B、C三者组成的系统动量守恒,有
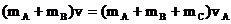
解得: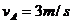
(2)B、C碰撞时B、C组成的系统动量守恒,设碰后瞬间B、C两者速度为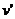 ,则
,则
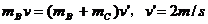
设物块A速度为vA时弹簧的弹性势能最大为EP,根据能量守恒
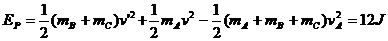
(3)由系统动量守恒得
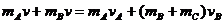
设A的速度方向向左,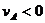 ,则
,则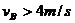
则作用后A、B、C动能之和
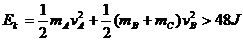
实际上系统的机械能
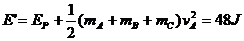
根据能量守恒定律,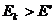 是不可能的。故A不可能向左运动。
是不可能的。故A不可能向左运动。
[模型要点]
系统动量守恒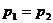 ,如果弹簧被作为系统内的一个物体时,弹簧的弹力对系统内物体做不做功都不影响系统的机械能。能量守恒
,如果弹簧被作为系统内的一个物体时,弹簧的弹力对系统内物体做不做功都不影响系统的机械能。能量守恒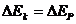 ,动能与势能相互转化。
,动能与势能相互转化。
弹簧两端均有物体:弹簧伸长到最长或压缩到最短时,相关联物体的速度一定相等,弹簧具有最大的弹性势能。
当弹簧恢复原长时,相互关联物体的速度相差最大,弹簧对关联物体的作用力为零。若物体再受阻力时,弹力与阻力相等时,物体速度最大。
[模型演练]
(2010年江苏省前黄高级中学检测题)如图4所示,在光滑水平长直轨道上,A、B两小球之间有一处于原长的轻质弹簧,弹簧右端与B球连接,左端与A球接触但不粘连,已知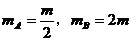 ,开始时A、B均静止。在A球的左边有一质量为
,开始时A、B均静止。在A球的左边有一质量为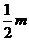 的小球C以初速度
的小球C以初速度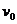 向右运动,与A球碰撞后粘连在一起,成为一个复合球D,碰撞时间极短,接着逐渐压缩弹簧并使B球运动,经过一段时间后,D球与弹簧分离(弹簧始终处于弹性限度内)。
向右运动,与A球碰撞后粘连在一起,成为一个复合球D,碰撞时间极短,接着逐渐压缩弹簧并使B球运动,经过一段时间后,D球与弹簧分离(弹簧始终处于弹性限度内)。
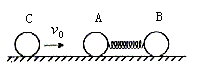
图4
(1)上述过程中,弹簧的最大弹性势能是多少?
(2)当弹簧恢复原长时B球速度是多大?
(3)若开始时在B球右侧某位置固定一块挡板(图中未画出),在D球与弹簧分离前使B球与挡板发生碰撞,并在碰后立即将挡板撤走,设B球与挡板碰撞时间极短,碰后B球速度大小不变,但方向相反,试求出此后弹簧的弹性势能最大值的范围。
答案:(1)设C与A相碰后速度为v1,三个球共同速度为v2时,弹簧的弹性势能最大,由动量守恒,能量守恒有:
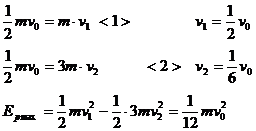
(2)设弹簧恢复原长时,D球速度为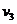 ,B球速度为
,B球速度为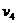
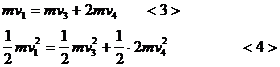
则有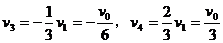
(3)设B球与挡板相碰前瞬间D、B两球速度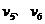
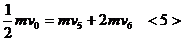
与挡板碰后弹性势能最大,D、B两球速度相等,设为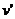
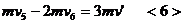
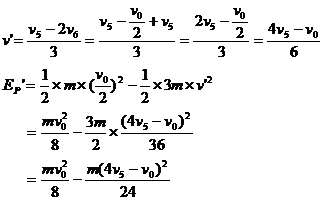
当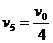 时,
时,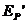 最大
最大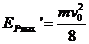
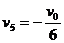 时,
时,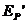 最小,
最小,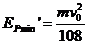
所以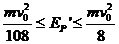
例3. 图2中,轻弹簧的一端固定,另一端与滑块B相连,B静止在水平直导轨上,弹簧处在原长状态。另一质量与B相同滑块A,从导轨上的P点以某一初速度向B滑行,当A滑过距离l1时,与B相碰,碰撞时间极短,碰后A、B紧贴在一起运动,但互不粘连。已知最后A恰好返回出发点P并停止,滑块A和B与导轨的滑动摩擦因数都为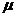 ,运动过程中弹簧最大形变量为l2,重力加速度为g,求A从P出发时的初速度v0。
,运动过程中弹簧最大形变量为l2,重力加速度为g,求A从P出发时的初速度v0。
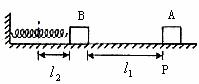
图2
解析:令A、B质量皆为m,A刚接触B时速度为v1(碰前)
由功能关系,有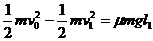
A、B碰撞过程中动量守恒,令碰后A、B共同运动的速度为v2
有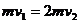
碰后A、B先一起向左运动,接着A、B一起被弹回,在弹簧恢复到原长时,设A、B的共同速度为v3,在这一过程中,弹簧势能始末状态都为零,利用功能关系,有
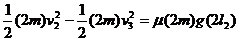
此后A、B开始分离,A单独向右滑到P点停下,由功能关系有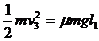
由以上各式,解得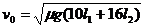
例2. 在原子核物理中,研究核子与核子关联的最有效途径是“双电荷交换反应”。这类反应的前半部分过程和下述力学模型类似,两个小球A和B用轻质弹簧相连,在光滑的水平直轨道上处于静止状态,在它们左边有一垂直于轨道的固定挡板P,右边有一小球C沿轨道以速度v0射向B球,如图1所示,C与B发生碰撞并立即结成一个整体D,在它们继续向左运动的过程中,当弹簧长度变到最短时,长度突然被锁定,不再改变,然后,A球与挡板P发生碰撞,碰后A、D都静止不动,A与P接触而不粘连,过一段时间,突然解除锁定(锁定及解除锁定均无机械能损失),已知A、B、C三球的质量均为m。
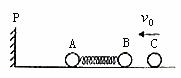
图1
(1)求弹簧长度刚被锁定后A球的速度。
(2)求在A球离开挡板P之后的运动过程中,弹簧的最大弹性势能。
解析:(1)设C球与B球粘结成D时,D的速度为v1,由动量守恒得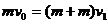 当弹簧压至最短时,D与A的速度相等,设此速度为v2,由动量守恒得
当弹簧压至最短时,D与A的速度相等,设此速度为v2,由动量守恒得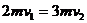 ,由以上两式求得A的速度
,由以上两式求得A的速度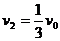 。
。
(2)设弹簧长度被锁定后,贮存在弹簧中的势能为EP,由能量守恒,有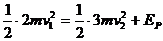 撞击P后,A与D的动能都为零,解除锁定后,当弹簧刚恢复到自然长度时,势能全部转弯成D的动能,设D的速度为v3,则有
撞击P后,A与D的动能都为零,解除锁定后,当弹簧刚恢复到自然长度时,势能全部转弯成D的动能,设D的速度为v3,则有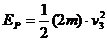
以后弹簧伸长,A球离开挡板P,并获得速度,当A、D的速度相等时,弹簧伸至最长,设此时的速度为v4,由动量守恒得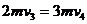
当弹簧伸到最长时,其势能最大,设此势能为EP',由能量守恒,有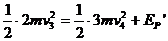 解以上各式得
解以上各式得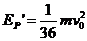 。
。
说明:对弹簧模型来说“系统具有共同速度之时,恰为系统弹性势能最多”。
例1. 在光滑水平地面上有两个相同的弹性小球A、B,质量都为m,现B球静止,A球向B球运动,发生正碰。已知碰撞过程中总机械能守恒,两球压缩最紧时的弹性势能为EP,则碰前A球的速度等于( )
A. 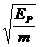 B.
B.
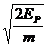 C.
C.
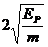 D.
D.
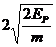
解析:设碰前A球的速度为v0,两球压缩最紧时的速度为v,根据动量守恒定律得出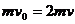 ,由能量守恒定律得
,由能量守恒定律得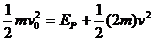 ,联立解得
,联立解得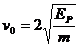 ,所以正确选项为C。
,所以正确选项为C。
4.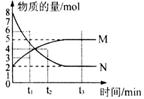 (1)一定温度下,容器内某一化学反应中M、N
(1)一定温度下,容器内某一化学反应中M、N
的物质的量随反应时间的变化的曲线如右图,则此反应的化学方程式为 ;此反应达到平衡时反应物的转化率 。
(2)在10℃和2×105pa的条件下,反应:aA(g)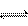 dD(g)+eE(g)建立平衡后,再逐步增大体系的压强(温度维持不变),表中列出不同压强下反应建立平衡时物质D的浓度。(已知反应过程中未出现物态变化。)
dD(g)+eE(g)建立平衡后,再逐步增大体系的压强(温度维持不变),表中列出不同压强下反应建立平衡时物质D的浓度。(已知反应过程中未出现物态变化。)
|
压强/pa |
2×105 |
4×105 |
|
D的浓度(mol/L) |
0.7 |
1.5 |
则压强由2×105增大到4×105时,平衡向 方向移动(填“正”或“逆”)。a与(d+e)的关系是:a (d+e)。(填“大于”、“小于”或“等于”。)
3.有mA(g)+nB(g) 3C(g)平衡体系,在不同条件下,反应混合物中A、B、C的体积分数和时间t的关系如图所示:
3C(g)平衡体系,在不同条件下,反应混合物中A、B、C的体积分数和时间t的关系如图所示:
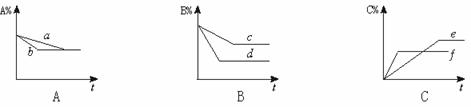
(1)若图A的a和b两条曲线分别表示有无催化剂的情形,曲线 表示有催化剂的情形。
(2)若图B中c、d两条曲线分别表示不同温度的情形,则曲线 表示高温时的情形。
(3)若图C中e、f表示不同压强时的情形,则曲线 表示压强较大时的情形,方程式中A、B两种物质的系数m、n分别为 、 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com