
4.下列各句中加点的熟语使用恰当的一项是
A.空谈误国,实干兴邦。要保持社会经济良好的发展态势,就必须力戒浮躁心态,坚决反对坐而论道,而应大力发扬求真务实的精神。
B.从亚锦赛的溃不成军到斯坦科维奇杯的屡遭绝杀,中国男篮最近的表现实难恭维,而教练郭士强的帅位也是风雨飘摇。
C.欧洲央行总裁特里谢称,全球金融危机标志着工业化国家的金融中心自二战以来首次面临泥牛入海的危险处境,必须通过各国央行和政府的共同努力来加以克服。
D.每逢年终岁末、辞旧迎新之时,央视春晚总是以其华美的演员服饰、专业化的灯光和音响以及令人回肠荡气的演员阵容而成为万千国民关注的焦点。
3.下列各句中,没有语病的一句是
A.最近,“被就业”成为新流行。有大学生说,自己在完全不知情的情况下突然就业了,就业协议书上赫然写着一个从没有听说过的公司名称和该公司的公章。
B.因受到新世纪流行文化和艺术的强烈冲击,又不太适应人们紧张繁忙的生活节奏,导致现在中国戏曲陷入不景气、就业率低、效益差的窘境。
C.近年来,名人故里之争不断,先有河南和湖北争抢“花木兰”,后又出现湖南、陕西争相标榜为“炎帝故乡”。名人故里之争实质上是利益驱动下的经济博弈,因为对名人故里的开发会带来可观的经济收入。
D.近年,中国政府在世界各地举办孔子学院,这一举措不仅促进了世界多元文化的发展,为构建和谐世界贡献力量,同时也增进世界人民对中国语言和文化的了解,进一步发展了中国与外国的友好关系。
2.下列各组词语中,没有错别字的一项是
A.雕饰 满堂采 时乖命蹇 公欲善其事,必先利其器
B.按揭 下脚料 坐收渔利 是可忍孰不可忍
C.鏖战 协奏曲 披波斩浪 凡事欲则立,不欲则废
D.勖勉 口头禅 志大才殊 无事不登三宝殿
1.下列词语中加点的字的读音,全都正确的一组是
A.焙(bèi)烧 靓(jìng)妆 晕(yùn)车 亟(jí)来问讯
B. 祓(fú)除 订(dìng)正 挑剔(tī) 春风骀(dài)荡
C.档(dǎng)案 解(xiè)数 下载(zài) 煊(xuǎn)赫一时
D 嫉(jí)恨 跻身(jǐ) 足癣(xuǎn) 抛头露(lù)面
1. 有一长为16米的篱笆,要围成一个矩形场地,则此矩形场地的最大面积为________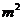 。
。
2
一个膨胀中的球形气球,其体积的膨胀率为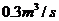 ,则其半径增至
,则其半径增至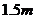 时,半径的增长率是________。
时,半径的增长率是________。
3 容积为256升的方底无盖水箱,它的高为________时最省材料
4 一窗户的上部是半圆,下部是矩形,如果窗户面积一定,当圆半径与矩形的高的比为________时,窗户周长最小。
5 若一球的半径为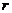 ,作内接于球的圆柱,则其侧面积最大为________。
,作内接于球的圆柱,则其侧面积最大为________。
6 以长为10的线段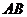 为直径作半圆,则它的内接矩形的面积的最大值为________。
为直径作半圆,则它的内接矩形的面积的最大值为________。
7用边长为48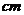 的正方形铁皮做一个无盖的铁盒时,在铁皮的四角各截去一个面积相等的小正方形,然后把四边折起,就能焊成铁盒,所做的铁盒容积最大时,在四角截去的正方形的边长为________。
的正方形铁皮做一个无盖的铁盒时,在铁皮的四角各截去一个面积相等的小正方形,然后把四边折起,就能焊成铁盒,所做的铁盒容积最大时,在四角截去的正方形的边长为________。
8将水注入圆锥形容器中,其速度为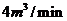 ,设圆锥形容器的高为
,设圆锥形容器的高为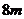 ,顶口直径为
,顶口直径为 ,求当水深为
,求当水深为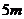 时,水面上升的速度。
时,水面上升的速度。
9 某厂生产某种电子元件,如果生产出一件正品可获利200元,如果生产出一件次品,则损失100元,已知该厂制造电子元件过程中,次品率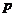 与日产量
与日产量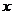 的关系是:
的关系是: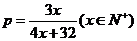
(1)求该厂的日盈利额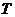 (元)用日产量
(元)用日产量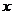 (件)表示的函数;
(件)表示的函数;
(2)为获最大盈利,该厂的日产量应定为多少件?
10统计表明,某种型号的汽车在匀速行驶中每小时耗油量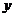 (升)关于行驶速度
(升)关于行驶速度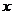 (千米/时)的函数解析式可以表示为
(千米/时)的函数解析式可以表示为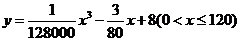 ,已知甲乙两地相距100千米。
,已知甲乙两地相距100千米。
(1) 当汽车以40千米/时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(2) 当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
例1 用长为18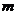 的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为
的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为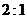 ,问:该长方体长,宽,高各为多少时,其体积最大?最大体积是多少?
,问:该长方体长,宽,高各为多少时,其体积最大?最大体积是多少?
例2 经过点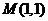 作直线
作直线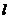 分别交
分别交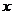 轴正半轴,
轴正半轴,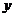 轴正半轴于
轴正半轴于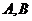 两点,设直线
两点,设直线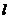 的斜率为
的斜率为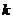 ,
,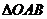 的面积为
的面积为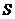
(1) 求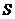 关于
关于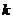 的函数关系式
的函数关系式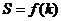 ;
;
(2) 求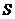 的最小值以及相应的直线
的最小值以及相应的直线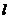 的方程。
的方程。
变式:有一隧道既是交通拥挤地段又是事故多发地段。为了保证安全,交通部门规定:隧道内的车距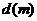 正比于车速
正比于车速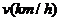 的平方与自身长
的平方与自身长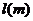 的积,且车距不得小于半个车身长。而当车速为60
的积,且车距不得小于半个车身长。而当车速为60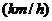 时,车距为
时,车距为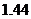 个车身长。在交通繁忙时,应规定车速为多少时可以使隧道的车流量最大。(选修2-2,
个车身长。在交通繁忙时,应规定车速为多少时可以使隧道的车流量最大。(选修2-2,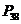 第4题)
第4题)
例3 某地有三家工厂,分别位于矩形ABCD的顶点A,B及CD的中点P处,已知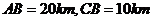 ,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且与A,B等距离的一点O处建造一个污水处理厂,并铺设排污管道
,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且与A,B等距离的一点O处建造一个污水处理厂,并铺设排污管道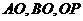 ,设排污管道的总长为
,设排污管道的总长为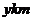 。
。
(1) 按下列要求写出函数关系式:
 ①设
①设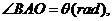 将
将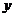 表示成
表示成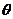 的函数关系式;
的函数关系式;
②设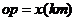 ,将
,将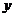 表示成
表示成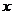 的函数关系式。
的函数关系式。
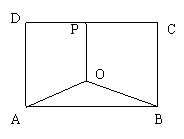 (2)请你选用(1)中的一个函数关系式确定污水处理厂的位置,使三条排污管道总长度最短。(2008年江苏高考)
(2)请你选用(1)中的一个函数关系式确定污水处理厂的位置,使三条排污管道总长度最短。(2008年江苏高考)
1. 周长为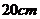 的矩形,绕一条边旋转成一个圆柱,则圆柱体积的最大值为________。
的矩形,绕一条边旋转成一个圆柱,则圆柱体积的最大值为________。
2 某产品的销售收入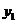 (万元)是产量
(万元)是产量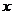 (千台)的函数:
(千台)的函数: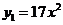 ,生产总成本
,生产总成本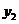 (万元)也是产量
(万元)也是产量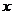 (千台)的函数:
(千台)的函数: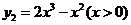 ,为使利润最大,应生产产品________台。
,为使利润最大,应生产产品________台。
3 一轮船以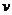 千米/时的速度航行,每小时用煤
千米/时的速度航行,每小时用煤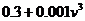 吨,
吨,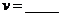 千米/时,才能使轮船航行每千米用的煤最少。
千米/时,才能使轮船航行每千米用的煤最少。
4 设正三棱柱的体积为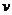 ,那么其表面积最小时的底面边长为________。
,那么其表面积最小时的底面边长为________。
5 某公司生产某种产品,固定成本为20000元,每生产一单位产品,成本增加100元,已知总收益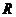 与年产量
与年产量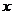 的关系是:
的关系是: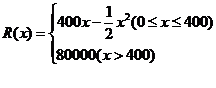 ,则总利润最大时,每年生产的产品是________个单位。
,则总利润最大时,每年生产的产品是________个单位。
解应用题的基本程序是:


 读题
建模
求解
反馈
读题
建模
求解
反馈
(文字语言) (数学语言) (导学应用) (检验作答)
利用导数解决生活中的优化问题的一般步骤:
① 分析实际问题中各量之间的关系,列出实际问题的数学模型,写出实际问题中变量之间的函数关系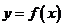 ;注意
;注意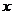 的范围。
的范围。
② 利用导数求函数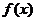 的极值和函数的最值;给出数学问题的解答。
的极值和函数的最值;给出数学问题的解答。
③ 把数学问题的解答转化为实际问题的答案。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com