
21.解:(1)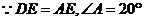
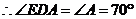 …………1分
…………1分
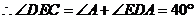 ………………………3分
………………………3分
(2)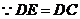 ,
,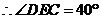
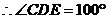 ,………………4分
,………………4分
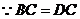
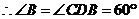 …………6分
…………6分
20.解:在Rt△ABC中,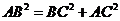 ………1分
………1分
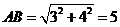 ………4分
………4分
少走了
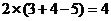 步………5分
步………5分
19.求出等式中的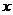 : (1)
: (1)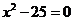 (2)
(2)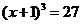
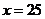 …………1分
…………1分 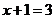 …………2分
…………2分
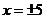 ………3分
………3分
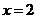 …………3分
…………3分
18.计算: 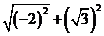
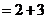 …………2分
…………2分
=5 …………3分
|
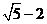 13.
13.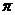
14.10cm 15.7 16.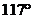 17. 3
17. 3
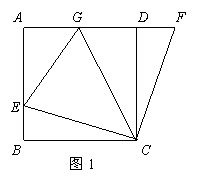
28.如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,
且△CBE≌△CDF.
(1)图1中的△CBE可以通过怎样的旋转得到△CDF;
(2)在图1中,若G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
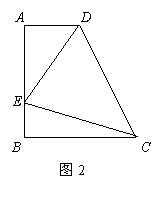
如图2,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=12,E是AB上一点,且∠DCE=45°,BE=4,求DE的长.
庆安县巨宝山中学2009-2010学年度第一学期期中
八年级数学试卷评分标准
注意:第27题每种情况2分,共6分.多一种情况加2分,全卷总分不超过100分.
27.有一块直角三角形的绿地,量得两直角边长分别为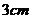 ,
,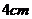 现在要将绿地扩充成等腰三角形,且扩充部分是以
现在要将绿地扩充成等腰三角形,且扩充部分是以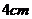 为直角边的直角三角形,请画出图形并直接写出扩充后等腰三角形绿地的周长.(友情提醒:不写画法,作图工具不限)
为直角边的直角三角形,请画出图形并直接写出扩充后等腰三角形绿地的周长.(友情提醒:不写画法,作图工具不限)
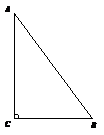



26.在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,图①、图②、图③均为顶点都在格点上的三角形(每个小方格的顶点叫格点).
(1) 在图1中,图①经过一次 变换(填“平移”或“旋转”或“轴对称”)可以
得到图②;
(2) 在图1中,图③是可以由图②经过一次旋转变换得到的,其旋转中心是点 (填“A”或“B”或“C”) ;
(3) 在图2中画出图①绕点A顺时针旋转90°后的图④.
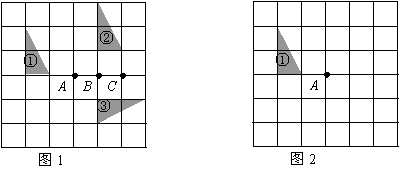
25.用四块如图(1)所示的正方形瓷砖拼成一个新的正方形,请你在(2)、(3)、(4)中各画一种拼法,使其分别满足以下条件:
(1) 图2是一个轴对称图形,但不是中心对称图形;
(2) 图3是一个中心对称图形,但不是轴对称图形;
(3) 图4既是轴对称图形,又是中心对称图形.
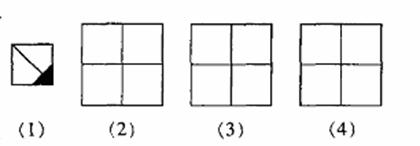
24.美国第二十届总统加菲尔德也曾经给出了勾股定理的一种证明方法,如图,他用两个全等的直角三角形和一个等腰直角三角形拼出了一个直角梯形,请你利用此图形验证勾股定理.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com