
5. 在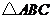 中,
中,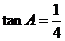 ,
,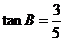 .
.
(Ⅰ)求角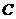 的大小;(Ⅱ)若
的大小;(Ⅱ)若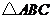 最大边的边长为
最大边的边长为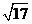 ,求最小边的边长.
,求最小边的边长.
4.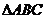 中,
中,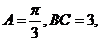 若.
若.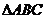 的周长可表示为
的周长可表示为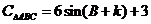 ,其中
,其中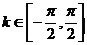 则实数
则实数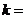 .
.
3. 在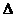 ABC中,
ABC中,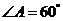 ,
,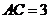 ,面积为
,面积为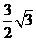 ,那么
,那么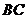 的长度为 .
的长度为 .
2. 已知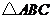 的周长为
的周长为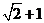 ,且
,且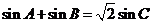 .则边
.则边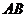 的长为
的长为
1. 在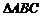 中,设
中,设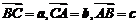 ,已知
,已知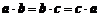 ,那么
,那么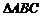 的形状为 .
的形状为 .
9. 解析:(1)由题设,可得=- ,则-sinBcosC=2cosBsinA+cosBsinC.
sinBcosC+cosBsinC+2cosBsinA=0,sin(B+C)+2cosB sinA=0,sinA+2cosB sinA=0.
因为sinA≠0 ,所以cosB=- ,所以B=120o.
(2)∵b2=a2+c2-2accosB,∴19=(a+c)2-2ac-2accos120o,∴ac=6.
又a+c=5,可解得或
三 范例剖析
例1 在△ABC中,a,b,c依次是角A,B,C所对的边,且4sinB·sin2(+)+cos2B=1+.
(1)求角B的度数;
(2)若B为锐角,a=4,sinC=sinB,求边c的长.
变题:在△ABC中,角A、B、C的对边分别为a、b、c.已知a+b=5,c =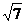 ,
,
且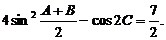
(1) 求角C的大小; (2)求△ABC的面积.
例2 在△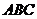 中,已知
中,已知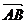 ·
·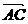 =9,sin
=9,sin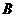 =cos
=cos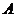 sin
sin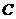 ,面积S
,面积S =6.
=6.
(1)求△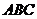 的三边的长;
的三边的长;
(2)设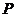 是△
是△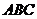 (含边界)内一点,
(含边界)内一点,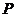 到三边
到三边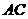 、
、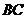 、
、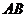 的距离分别为x,y和z,求x+y+z的取值范围.
的距离分别为x,y和z,求x+y+z的取值范围.
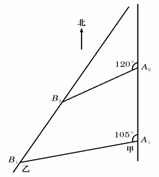 例3(07山东)如图,甲船以每小时30
例3(07山东)如图,甲船以每小时30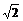 海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A1处时,乙船航行到甲船的北偏西120°方向的B1处,此时两船相距10
海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A1处时,乙船航行到甲船的北偏西120°方向的B1处,此时两船相距10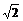 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?
四 巩固训练
8. 解析: 由余弦定理,得 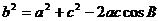 .则
.则
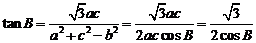 ,即
,即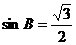 .
.
所以B的大小是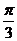 或
或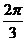 .
.
7.由正弦定理,原式=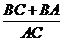 ,又由椭圆定义知:
,又由椭圆定义知: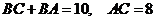
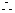 原式=
原式=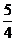
6.由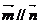
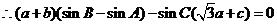 ,
,
由正弦定理有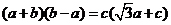 即
即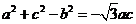 ,
,
再由余弦定理得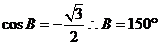
5.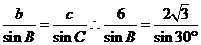 即
即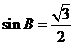
又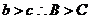 ,C为锐角,所以两解
,C为锐角,所以两解
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com