
4.分层抽样:
(1)将总体按一定标准分层;
(2)计算各层的个体数与总体的个数的比;
(3)按各层个体数占总体的个体数的比确定各层应抽取的样本容量;
(4)在每一层进行抽样(可用简单随机抽样或系统抽样).
3.系统抽样(等距抽样):
(1)采用随机的方式将总体中的个体编号;
(2)将整个的编号按一定的间隔(设为k)分段,当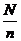 (N为总体中的个体数,n为样本容量)是整数时,
(N为总体中的个体数,n为样本容量)是整数时,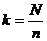 ;当
;当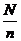 不是整数时,从总体中剔除一些个体,使剩下的总体中个体的个数N
不是整数时,从总体中剔除一些个体,使剩下的总体中个体的个数N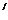 能被n整除,这时
能被n整除,这时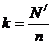 ,并将剩下的总体重新编号;
,并将剩下的总体重新编号;
(3)在第一段中用简单随机抽样确定起始的个体编号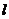 ;
;
(4)将编号为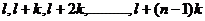 的个体抽出.
的个体抽出.
2.随机数表法:
(1)对总体中的个体进行编号(每个号码位数一致);
(2)在随机数表中任选一个数作为开始;
(3)从选定的数开始按一定的方向读下去,得到的数码若不在编号中,则跳过;若在编号中,则取出;如果得到的号码前面已经取出,也跳过;如此继续下去,直到取满为止;
(4) 根据选定的号码抽取样本.
1.抽签法:
(1)将总体中的所有个体编号(号码可以从1到N);
(2)将1到N这N个号码写在形状、大小相同的号签上(号签可以用小球、卡片、纸条等制作);
(3)将号签放在同一箱中,并搅拌均匀;
(4)从箱中每次抽出1个号签,并记录其编号,连续抽取k次;
(5)从总体中将与抽到的签的编号相一致的个体取出.
12.1抽样方法
5.解下列方程:
(1)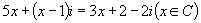 ;
;
(2)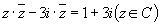 .
.
第十二章 统计
4.计算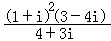
3.计算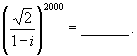
2.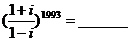
[例1] 满足条件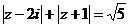 的点的轨迹是( )
的点的轨迹是( )
A.椭圆 B.直线 C.线段 D.圆
错解:选A或B.
错因:如果把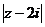 看作动点Z到定点(0,2)的距离,由上式表示到两个定点(0,2)与(-1,0)的距离之和为常数
看作动点Z到定点(0,2)的距离,由上式表示到两个定点(0,2)与(-1,0)的距离之和为常数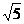
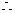 动点的轨迹符合椭圆的定义,但是,有一定的前提的就是两点间的距离小于定常数.
动点的轨迹符合椭圆的定义,但是,有一定的前提的就是两点间的距离小于定常数.
正解: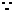 点(0,2)与(-1,0)间的距离为
点(0,2)与(-1,0)间的距离为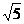 ,
,
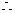 动点在两定点(0,-2)与(-1,0)之间,选C
动点在两定点(0,-2)与(-1,0)之间,选C
评注:加强对概念的理解加深,认真审题.
[例2] 求值: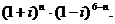
错解:原式=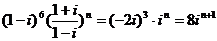
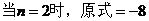
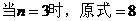
错因:上面的解答错在没有真正理解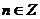 的含义,只是用了三个特殊整数代替了所有整数,犯了用特殊代替一般的错误.另外还可以看出对虚数单位
的含义,只是用了三个特殊整数代替了所有整数,犯了用特殊代替一般的错误.另外还可以看出对虚数单位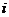 的整数幂的运算不熟悉,没有掌握虚数单位
的整数幂的运算不熟悉,没有掌握虚数单位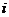 整数幂的运算结果的周期性.
整数幂的运算结果的周期性.
正解:原式=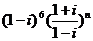
=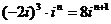
=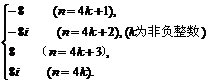
评注:虚数单位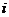 整数幂的值具有以4为周期的特点,根据
整数幂的值具有以4为周期的特点,根据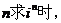 必须按被4整除余数为0、1、2、3四种情况进行分类讨论.
必须按被4整除余数为0、1、2、3四种情况进行分类讨论.
[例3]已知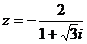 ,求
,求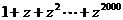 的值.
的值.
分析:结论是等比数列的求和问题,所以应联想到求和公式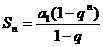 ,若直接将条件代入求和公式,则显得较为麻烦,不妨先将条件化简.
,若直接将条件代入求和公式,则显得较为麻烦,不妨先将条件化简.
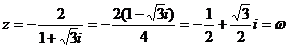
原式=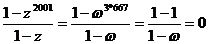
评注:由于数列中的数可以是复数,所以数列的诸性质在复数集中仍成立.
[例4]已知复数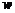 满足
满足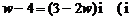 为虚数单位),
为虚数单位),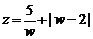 ,求一个以
,求一个以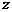 为根的实系数一元二次方程.
为根的实系数一元二次方程.
解法一: 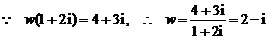 ,
,
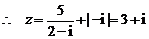 .
.
若实系数一元二次方程有虚根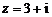 ,则必有共轭虚根
,则必有共轭虚根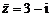 .
.
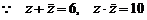 ,
,
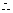 所求的一个一元二次方程可以是
所求的一个一元二次方程可以是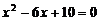 .
.
解法二:设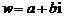
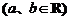
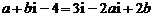 ,
,
得 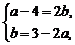
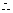
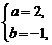
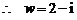 ,
,
以下解法同解法一.
[例5]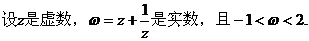
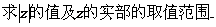
解析 
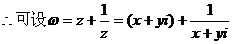
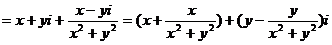
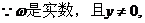
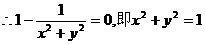
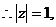
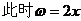
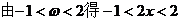
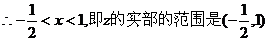
四、典型习题导练
1.非空集合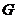 关于运算
关于运算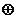 满足:(1)对任意
满足:(1)对任意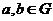 ,都有
,都有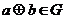 ;
;
(2)存在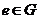 ,使得对一切
,使得对一切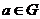 ,都有
,都有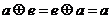 ,则称
,则称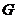 关于运算
关于运算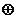 为“融洽集”;现给出下列集合和运算:
为“融洽集”;现给出下列集合和运算:
①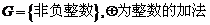
②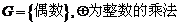
③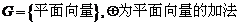
④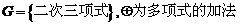
⑤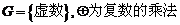
其中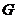 关于运算
关于运算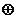 为“融洽集”__________;(写出所有“融洽集”的序号)
为“融洽集”__________;(写出所有“融洽集”的序号)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com