
2.在进行复数的运算时,不能把实数的某些法则和性质照搬到复数集中来,如下面的结论.
当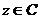 时,不总是成立的.
时,不总是成立的.
(1)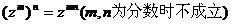 ;
;
(2)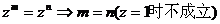 ;
;
(3)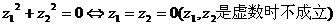 ;
;
(4)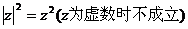 ;
;
(5)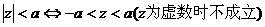
1.对于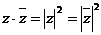 ,是复数运算与实数运算相互转化的主要依据,也是把复数看作整体进行运算的主要依据,在解题中加以认识并逐渐体会.
,是复数运算与实数运算相互转化的主要依据,也是把复数看作整体进行运算的主要依据,在解题中加以认识并逐渐体会.
2. 重要结论
(1) 对复数z 、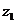 、
、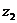 和自然数m、n,有
和自然数m、n,有
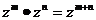 ,
,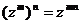 ,
,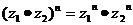
(2) 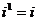 ,
,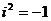 ,
,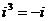 ,
,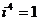 ;
;
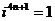 ,
,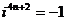 ,
,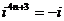 ,
,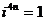 .
.
(3) 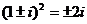 ,
,
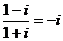 ,
,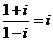 .
.
(4)设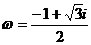 ,
,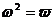 ,
,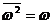 ,
,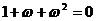 ,
,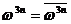 ,
,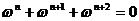
1.复数加、减法的几何意义
(1)加法的几何意义
复数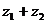 是以
是以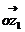 、
、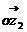 为两邻边的平行四边形对角线
为两邻边的平行四边形对角线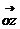 所对应的复数.
所对应的复数.
(2)复数减法的几何意义
复数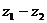 是连接向量
是连接向量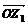 、
、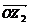 的终点,并指向被减数的向量
的终点,并指向被减数的向量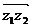 所对应的复数.
所对应的复数.
5.设复数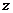 满足
满足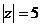 且
且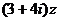 在复平面上对应的点在第二象限、四象限的角平分线上,
在复平面上对应的点在第二象限、四象限的角平分线上,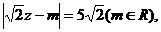 求
求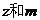 的值
的值
§11.2 复数的运算
4.已知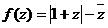 且
且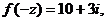 求复数
求复数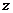
3. 实数m取何值时,复数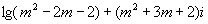 是(1)纯虚数;(2)在复平面上的对应点位于第二象限.
是(1)纯虚数;(2)在复平面上的对应点位于第二象限.
2.复数系方程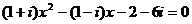 有实数根,则这个实数是
有实数根,则这个实数是 .
.
1. 设复数z满足关系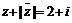 ,那么z等于( ).
,那么z等于( ).
A.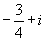 B.
B.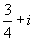 C.
C.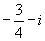 D.
D.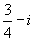
[例1]两个共扼复数的差是( )
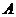 .实数
.实数 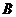 .纯虚数
.纯虚数 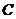 .零
.零 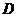 .零或纯虚数
.零或纯虚数
错解:当得到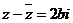 时就错误的选B,忽略了b可以为零的条件.
时就错误的选B,忽略了b可以为零的条件.
正解:设互为共扼的两复数分别为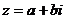 及
及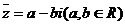 则
则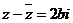 或
或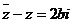
当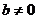 时,
时,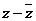 ,
,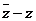 为纯虚数
为纯虚数
当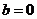 时,
时,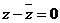 ,
,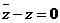 ,因此应选D.
,因此应选D.
注:要认真审题,看清题设条件,结论. 学会全面辩证的思考问题,准确记
忆有关概念性质.
[例2]判断下列命题是否正确
(1)若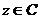 , 则
, 则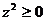
(2)若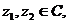 且
且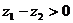 ,则
,则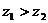
(3)若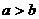 ,则
,则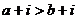
错解:(1)认为任何一个实数的平方大于零可推广到复数中,从而(1)是正
确的
(2)认为两实数之差大于零等价于前一个大于后一个实数,也可推到复
数中来.认为两复数差为实数则这两个复数也为实数.而认为命题(2)是正确的.
(3)把不等式性质错误的推广到复数中,忽略不等式是在实数中成立的
前提条件.
正解:(1)错,反例设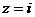 则
则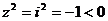
(2)错,反例设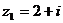 ,
,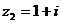 ,满足
,满足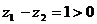 ,但
,但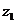
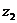
不能比较大小.
(3)错,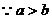 ,
,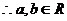 ,故
,故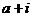 ,
,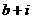 都是虚数,不能比较大小.
都是虚数,不能比较大小.
[例3]实数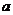 分别取什么值时,复数
分别取什么值时,复数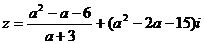 是(1)实数;
是(1)实数;
(2)虚数;(3)纯虚数.
解:实部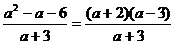 ,虚部
,虚部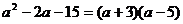 .
.
(1)当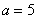 时,
时,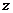 是实数;
是实数;
(2)当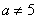 ,且
,且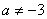 时,
时,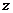 是虚数;
是虚数;
(3) 当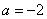 或
或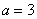 时是纯虚数.
时是纯虚数.
[例4] 设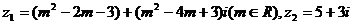 ,当
,当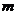 取何值时,
取何值时,
(1) 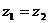 ; (2)
; (2)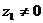 .
.
分析:复数相等的充要条件,提供了将复数问题转化为实数问题的依据,这是解复数问题常用的思想方法,这个题就可利用复数相等的充要条件来列出关于实数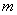 的方程,求出
的方程,求出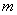 的值.
的值.
解:(1)由可得: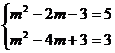 解之得
解之得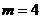 ,
,
即:当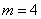 时
时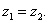
(2)当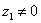 可得:
可得:
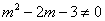 或
或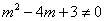 ,即
,即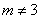 时
时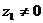 .
.
[例5]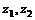 是两个不为零的复数,它们在复平面上分别对应点P和Q,且
是两个不为零的复数,它们在复平面上分别对应点P和Q,且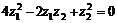 ,证明△OPQ为直角三角形(O是坐标原点),并求两锐角的度数.
,证明△OPQ为直角三角形(O是坐标原点),并求两锐角的度数.
分析 本题起步的关键在于对条件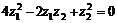 的处理.等式左边是关于
的处理.等式左边是关于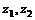 的二次齐次式,可以看作二次方程求解,也可配方.
的二次齐次式,可以看作二次方程求解,也可配方.
解:由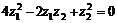 (
(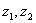 ,不为零),
,不为零),

 得
得


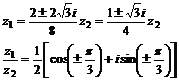
即向量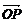 与向量
与向量 的夹角为
的夹角为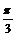 ,
,
在图中,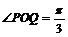 ,又
,又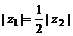 ,设
,设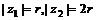 ,
,
在△OPQ中,由余弦定理
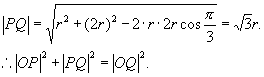
△OPQ为直角三角形,
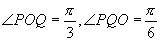 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com