
[例1]某人5次上班途中所花的时间(单位:分钟)分别为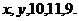 已知这组数据的平均数为10,方差为2,则
已知这组数据的平均数为10,方差为2,则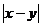 的值为(
)
的值为(
)
A.1 B.2 C.3 D.4
解:由平均数公式为10,得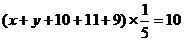 ,则
,则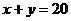 ,又由于方差为2,则
,又由于方差为2,则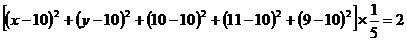 得
得
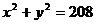
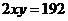
所以有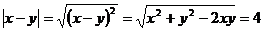 ,故选D.
,故选D.
[例2]数据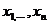 是一名运动员的
是一名运动员的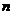 次射击的命中环数,则他的平均命中环数的估计是( ).
次射击的命中环数,则他的平均命中环数的估计是( ).
A.样本平均数均值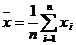 B.样本极差
B.样本极差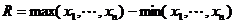
C.样本方差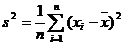 D.样本平均差AD=
D.样本平均差AD=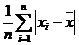
错解:C.
错因:后三个选项都表示了样本的波动程度,不能用于总体平均值的估计.
正解:A.
[例3]某房间中10个人的平均身高为1.74米,身高为1.85米的第11个人,进入房间后,这11个人的平均身高是多少?
解:原来的10个人的身高之和为17.4米,所以,这11个人的平均身高为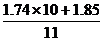 =1.75.即这11个人的平均身高为1075米
=1.75.即这11个人的平均身高为1075米
[例4]若有一个企业,70%的人年收入1万,25%的人年收入3万,5%的人年收入11万,求这个企业的年平均收入及年收入的中位数和众数
解:年平均收入为1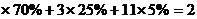 (万);中位数和众数均为1万
(万);中位数和众数均为1万
[例5]下面是某快餐店所有工作人员的收入表:
|
老板 |
大厨 |
二厨 |
采购员 |
杂工 |
服务生 |
会计 |
|
3000元 |
450元 |
350元 |
400元 |
320元 |
320元 |
410元 |
(1)计算所有人员的月平均收入;
(2)这个平均收入能反映打工人员的月收入的一般水平吗?为什么?
(3)去掉老板的收入后,再计算平均收入,这能代表打工人员的月收入的水平吗?
(4)根据以上计算,以统计的观点对(3)的结果作出分析
解:(1)平均收入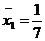
4.样本方差也可以用公式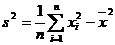 计算.
计算.
3.分布的分散程序还可以用极差来描述,但较粗略.
2.方差和标准差是总体的数字特征,反映了分布的分散程序(波动大小),标准差也会受极端值(特别大或特别小的值)的影响.
1.平均数,中位数和众数都是总体的数字特征,从不同角度反映了分布的集中趋势,平均数是最常用的指标,也是数据点的“重心”位置,它易受极端值(特别大或特别小的值)的影响,中位数位于数据序列的中间位置,不受极端值的影响,在一组数据中,可能没有众数,也可能有多个众数.
4.
一般地,设一组样本数据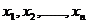 ,其平均数为
,其平均数为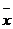 ,则称
,则称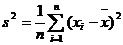 为这个样本的方差,算术平方根
为这个样本的方差,算术平方根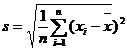 为样本的标准差,分别简称样本方差,样本标准差.
为样本的标准差,分别简称样本方差,样本标准差.
3.把一组数据的最大值与最小值的差称为极差.
2.一般地,若取值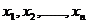 的频率分别为
的频率分别为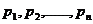 ,则其平均数为
,则其平均数为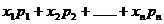 .
.
1.n 个数据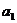 ,
,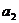 ,…….
,…….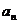 的平均数或平均值一般记为
的平均数或平均值一般记为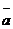 =
=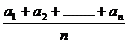 .
.
12.3平均数、方差与标准差
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com